
- •Содержание 2
- •Введение. 136
- •2. Введение
- •1. Основные понятия
- •1.1 Моделирование. Основные понятия.
- •1.1.1 Системный анализ и моделирование
- •1.1.2 Концептуальные модели.
- •1.1.3 Термины и определения
- •1.1.4 Формализация и алгоритмизация процессов.
- •1.2 Математическое моделирование
- •1.2.1 Классификация математических моделей.
- •Классификация математических моделей на основе особенностей применяемого математического аппарата
- •1.2.2 Основной принцип классификации математических моделей
- •1.2.3 Программирование модели
- •1.2.4 Испытание модели
- •1.2.5 Исследование свойств имитационной модели.
- •Эксплуатация имитационной модели.
- •Анализ результатов моделирования.
- •1.3 Виды анализа и расчета электронных схем
- •1.4 Модели элементов и схем
- •2. Модели компонентов электронных схем
- •2.1 Классификация моделей
- •2.2 Интерполяция и аппроксимация функций при создании моделей
- •2.2.1 Интерполяция функций
- •2.2.2 Аппроксимация функций
- •2.3 Модели основных электронных компонентов
- •2.3.1 Базовый набор элементов моделей
- •2.3.2 1.1 Резистор
- •1. Пассивные компоненты и их модели
- •2.3.3 1.2 Конденсатор
- •2.3.4 Реальные конденсаторы
- •2.3.5 Катушка индуктивности и дроссель
- •2.3.6 Реальная индуктивность
- •2.3.7 Модели полупроводниковых приборов
- •2.4 Модели аналоговых компонентов программы Micro-Cap
- •2.4.1 Общие сведения о моделях компонентов
- •2.4.2 Пассивные компоненты
- •2.4.3 Резистор (Resistor)
- •Разброс сопротивления при использовании Monte-Carlo
- •3. Матрично-векторные параметры схем
- •3.1 Основные законы электрических цепей в матричном виде
- •3.2 Метод контурных токов
- •3.3 Метод узловых потенциалов
- •3.4 Метод обобщенных ветвей
- •3.5 Статический анализ линейных и нелинейных схем
- •3.6 Гибридный анализ электронных схем
- •4. Методы анализа переходных процессов
- •4.1 Введение
- •4.2 Литература
- •4.3 Основные задачи анализа переходных процессов
- •4.4 Анализ переходных процессов в линейных цепях
- •4.5 Анализ переходных процессов в нелинейных схемах и численные методы интегрирования нелинейных ду
- •4.5.1 Общие сведения о численных методах решения систем дифференциальных
- •4.5.7 Сведение расчета переходных процессов в электронных цепях к расчету цепей по постоянному току
- •4.6 Анализ переходных процессов в цепях с периодической
- •4.6.3 Дискретное преобразование Лапласа и его основные свойства
- •9. Теорема дифференцирования по параметру
- •10. Теорема интегрирования по параметру
- •11. Теорема об умножении изображений (теорема свертывания в вещественной области).
- •4.6.4 Решение линейных разностных уравнений
- •4.7 Параметрические цепи
Параметры
kj,
k2, кз
Параметры
S,
b,
p,
U0.
Тангенциальная
аппроксимация
где
M =
Is
• 1 + th S-{U3U
- wS )
I
кл'
i
л
k
'
i
л
k
Рис.
4.46
I
с = M
• 1
- e
M
f -
k
U „
, - S
\
ЛЛ
J)
Параметры
аппроксимации:
Is,
Us,
S, k.
Для
аппроксимации всех перечисленных
нелинейностей требуется определить
несколько коэффициентов, которые обычно
определяются на практике методом
выбранных точек.
Для его использования выбирают исходя
из физических соображений рабочий
участок вольт- амперной или иной
характеристики нелинейного элемента
и на нем — ряд точек, через которые
будет проходить аппроксимирующая
кривая. В число этих точек, как правило,
входят точки, соответствующие границам
рабочего интервала и характерные точки
ВАХ.
Число
точек равно числу неизвестных
коэффициентов аппроксимации. Далее в
аппроксимирующее выражение
подставляются значения функции в
указанных точках и решается система
уравнений относительно требуемых
коэффициентов. Такой метод весьма
прост, однако он гарантирует совпадение
аппроксимирующей функции с реальной
только в выбранных точках. Общая
погрешность метода непредсказуема.
Поэтому он применяется в случаях, когда
общий вид аппроксимирующей характеристики
и аппроксимируемой функции достоверно
известен.
Рассмотрим,
например выражение для спада емкости
электролитического конденсатора от
частоты и определение коэффициентов
аппроксимации:
С
С
=
/ \а 1
+
Vf0
J
Предположим,
что нам известна номинальная емкость
конденсатора
с0.
Тогда из Tpex коэффициентов
аппроксимации остается найти только
2. Берем частоты аппроксимации fj
и f2.
Емкости,
соответствующие этим частотам cj
и
с2
соответственно. Составляем систему
уравнений:
u
178
/
2
£
,
/
2
V
£
0 У
л Г
0 Г2
С
/
Л
V
f
2
у
dx
dt
Q
=
Cn
Сг
=
1
+
1+
' /
.s
l
а
'
£
л
Выразим
из нее соотношения V £°
у и
v
£оу
'
/Va
С
- с
Поделим
почленно оба выражения. Получим:
'S
/ \ а
fo
-
С-1
) • С 2
V
f
0
У " ( О , л
2 )
Логарифмируя
обе части выражения и проведя элементарные
преобразования полу-
чаем:
ln
а
=
(
с р С 1 ) • С 2
.(О,
- Сл
)• Q
ln
Выразим
далее частоту/о
через, например, Ci
и
/1.
Получим
С
- С . Q .
Рассмотрим
методы расчета переходных процессов
в нелинейных цепях. Аналитические
методы расчета основаны на замене
нелинейной характеристики аналитическим
выражением с приемлемой точностью. Ряд
подобных аппроксимаций уже рассмотрен,
хотя практическое их использование в
ряде случаев затруднительно вследствие
сложности полученных функций. Для
грубых прикидочных расчетов зачастую
применяют
метод линеаризации одной прямой.
уравнений
1-го порядка
Численное
решение переходных процессов в
электронных схемах сводится к численному
решению задачи Коши, т.е. к решению
обыкновенного дифференциального
уравнения или системы уравнений,
записанных в форме Коши, в явном виде:
=
F
(x, t, v)
или
в неявной форме:
с
л
V
0
У
V
0
У
С
1
V
' 0 У
/
1
/
0
179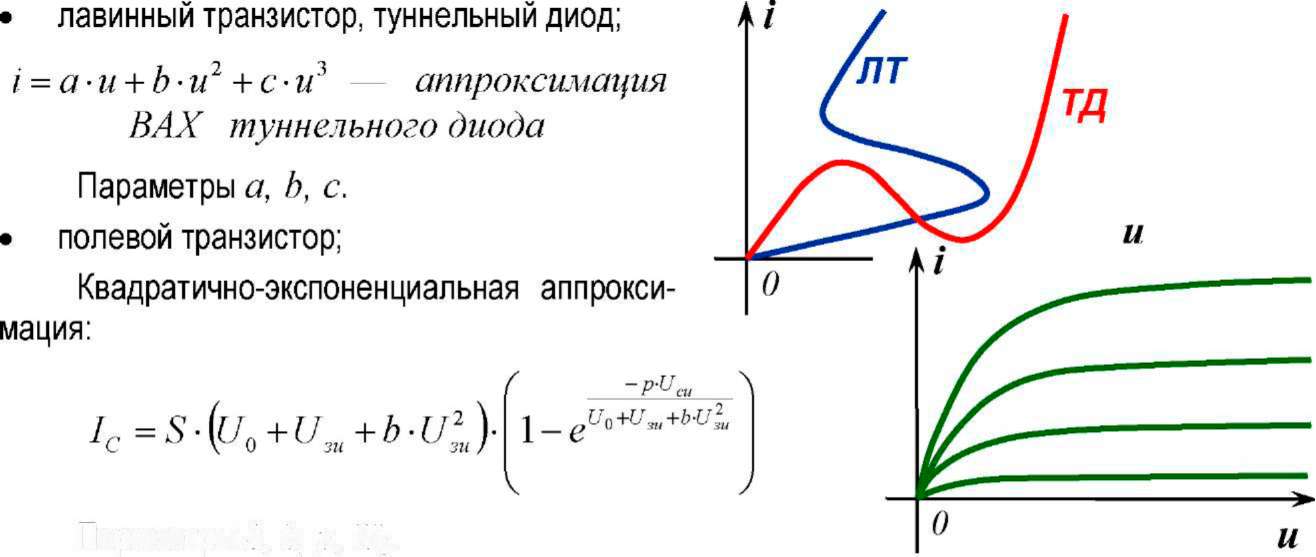
4.5.1 Общие сведения о численных методах решения систем дифференциальных
A
dx ±
„л
dx n x,
— , t, V — = 0 \ dt dt
Здесь
x
— вектор переменных состояния, t
— время, V — вектор
независимых источников.
Анализ
показывает, что решение дифференциального
уравнения существует и является
единственным, если правая часть
дифференциального уравнения непрерывна
в рассматриваемой области изменения
аргумента и удовлетворяет условию
Липшица:
гп
f
л
t
,
V)- f
t.
v
)\<
N
-X I
Xk ~Цк
k=
1
Здесь
ц — вектор, принадлежащий указанной
области изменения переменных, N —
некоторая положительная константа, m
— порядок системы.
Для
реальных электронных схем условие
существования и единственности решения
задачи Коши выполняется всегда.
Методы
численного интегрирования называются
пошаговыми, т.к. решение дифферен-
циальногоуравненияполучается как
результатвыполнения серии шагов по
осинезависимой переменной
t.
При
этом интервал интегрирования разбивается
на ряд интервалов точками t0=0,
t1,
t2,...tn=T.
Таким образом, непрерывный интервал
0...Тзаменяется дискретным множеством
точек tk.
Расстояние между точками есть
величина шага интегрирования h
= tk+1-tk.
Очередной
(k+1) шаг интегрирования
есть вычисление вектора x(tk+1),
причем при условии, что x(t1),
x(t2),
... x(tk)
уже вычислены в результате
предшествующих шагов. Формулы для
нахождения x(tk+1)
получаются в результате замены
производных в уравнении Коши на отношение
конечных приращений:
dx,
X- x • dt tk+1
- tk
Таким
образом, фактически, исходные
дифференциальные уравнения заменяются
конечно-разностными уравнениями.
При соответствующих допущениях в выборе
шага интегрирования, численное
решение конечно-разностных уравнений
будет достаточно точно совпадать с
решением соответствующих дифференциальных
уравнений. Итерационные формулы для
решения дифференциальных уравнений
получают, разлагая в ряд Тейлора функции
и отбрасывая соответствующее число
членов разложения. В зависимости от
количества оставленных членов
говорят о методах 1-го, 2-го и т.д. порядка.
Существуют
две группы методов численного решения
задачи Коши:
Одношаговые
методы, в которых для нахождения
последующей точки на кривой x(t)
используется
информация лишь об одном предыдущем
шаге;
Многошаговые
методы, в которых для отыскания
последующей точки требуется информация
о нескольких предыдущих точках расчета.
4.5.2
Одношаговые методы
Простейшим
из одношаговых методов решения
дифференциальных уравнений 1-го порядка
является
метод Эйлера (метод Рунге-Кутта первого
порядка).
Напомним, что задачей является
решение дифференциального уравнения
вида:
180
dx
dt
Таким
образом, итерационная формула для
нахо-
ждения
xk
+
1
готова.
Ошибка, полученная в результате
итерации,
очевидно, пропорциональна
h2.
Геометриче-
ская
интерпретация метода состоит в следующем
(рис.
4.47).
Замена
реальной кривой
x(t)
на
отрезки прямых,
соответствующих
касательным в точках
tk,
даст
при-
ближенное значение искомойфункции
xk
+
1.
Т.к.
ошибка
Рио
44 7
. метода
относительно велика, то для ее устранения
обычно
выбирают меньший шаг h,
но
в целом метод имеет ограниченное
применение, несмот-
ря на свою
простоту.
Модифицированный
метод Эйлера
Для
уменьшения погрешности за счет замены
функции
x(t)
отрезками
касательных, при-
меняют
модифицированный метод Эйлера.
Суть его сводится к тому, что значение
произ-
водной
F(x,t,v)
на
интервале
tk...tk+1
заменяют
полусуммой производных в начале и
конце
интервала:
F(xk,tk,v);
F(x3k+1,tk+1
,v).
При
этом значение переменной
xsk
+
:
в
конце интервала
вычисляют используя
предварительно, например, метод Эйлера.
Алгоритм работы модифици-
рованного
метода Эйлера таков:
Определяют
xak+1-xk
+
h-F(Xk,tk,v)
Затем
вычисляют уточненное значение вектора
переменных xM3k+1
по формуле:
xkM+3
-
x
+1
\ f
x ,
tk,
v)+
F x + 1,
f -1,
v)]
=
F
(x, t, v)
с
начальными условиями
x°-x(t°).
Разложим
функцию
x(t)
в
окрестности точки
tk
в
ряд Тейлора и найдем ее значение в
точке
х
(tk+h):
x
(tk +
h )- x
[tk)
+ h •
x{tk)
+
1 h2
•
x
\tk)+...
+
—hx(n}
[t)
+...
n!
L '
Если
h
мало,
то члены, содержащие степени h
выше
первой будем считать малыми и
пренебрежем
ими. Получим:
x(tk+1
)- x{tk
)+
h
•
F
(x(tk
),
tk,
v )
xk+1
-
xk
+
h
•
F[xk,tk,
v)
|
x |
|
|
|
к+1 |
|
|
|
|
x |
|
Г'1 |
|
|
xk |
/ |
i |
|
t |
|
о |
tk tk+i |
|
|
h
Можно показать, что модифицированный метод Эйлера является фактически методом второго порядка (Рунге-Кутта). Разложим x(t) в ряд Тейлора в окрестности точки tk и вычислим значение x(tk+h):
x t + h)- x(tk) + h^ F(xk,tk,v) + 1 • h2 • F (xk,tk,v)+...
Оставим три члена разложения и заменим производную F'(xk,tk,v) конечной разностью
первого порядка:
или
181
Рис.
4.48
Как
показано на примере метода Эйлера и
модифицированного метода Эйлера,
использование нескольких членов
разложения x(t)
в ряде Тейлора существенно уменьшает
погрешность интегрирования
дифференциальных уравнений. Для
использования n членов
разложе- ниянеобходимо, очевидно, иметь
представления (n-1)
производнойфункции F(x,t,v)
ввиде
конечных
разностей, а для этого, в свою очередь,
необходимо знание первой и более высоких
производных в промежуточных точках
интервала tk...tk+1.
С ростом порядка вычислений, очевидно,
число дополнительных вычислений на
каждом шаге интегрирования возрастает.
Существует несколько способов выбора
внутренних точек для вычисления
приближенных значений высших производных,
поэтому методы Рунге-Кутта объединяют
целое семейство методов. Наиболее
распространен метод Рунге-Кутта
четвертого порядка, в котором используются
все члены разложения, включая члены,
содержащие h4.
Расчеты производятся по формулам:
=
xk
+
- •[k
+
2 • k2
+
2 • k3
+
k4
]
6
4 **,tk,V)=
F
(x*+1,
tk
+
h,
v )
- F
(xk,
tk.
v )
h
Подставляя
ее значение в формулу для x(tk+h),
получим:
x(tk
+
h
)=
x(tk)+-
h -[F (x*+1,tk+1,
v)
+ F(x
,
t
,
V
Для
определения x.3k+1,
как и было сказа-
но выше,
используется простой метод
Эйлера.
Модифицированный метод
Эйлера гарантирует
наличие ошибки
не более h3.
Однако такое по-
)]
ХМЭ
вышение
точности достигается путем увеличения
k+1
вычислительных
затрат за счет вычисления x3
и
функции F(x3k+1,tk+1,v).
Геометрическая ин-
терпретация
метода имеет вид рис. 4.48.
Методы
Рунге-Кутта
t
0
,.k+1
'
pk
k1
=
h
•
F
\xk,
tk,
v )
k2
=
h
•
F(xk
+
0,5 • k1,
tk +
0,5 • h, v) k3
= h • F (.
+ 0,5 • k2,
tk +
0,5 • h, v) k
4
= h • F (: k
+ k3,
tk +
h, v)
Более
высокая точность метода Рунге-Кутта
позволяет увеличивать шаг интегрирования,
что в целом дает лучшую точность расчетов
при заданной погрешности. В ряде случаев
шаг интегрирования делают переменным.
С точки зрения алгоритма интегрирования
это не приводит к каким-либо
противоречиям. Погрешность вычислений
оценивают путем интегрирования
дифференциальных уравнений с шагом h
и, затем 2h.
Если x1
— значение вектора
x,
полученного при шаге
h,
a
x2
— значение при шаге 2h,
то получаемая погрешность оценивается
нормой вектора \\x
1
(tk)
- x2(tk)\.
Если норма вектора больше s
— заданной погрешности, то шаг
уменьшают вдвое, если она меньше
s/6,
то шаг увеличивают вдвое. Если норма
находится в интервале
s/6
...
s,
то величину шага оставляют прежней.
182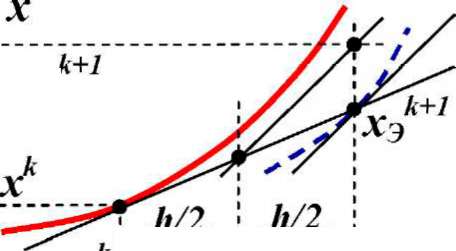
Р0„
,,
tk
)-
1
k —
второго порядка
-. л
PAti,
tj, tk)-p{tj,
tk, tt)
P{t1,
tj, tk,
t j
— —
третьего порядка и т.д.
Следует
отметить, что контроль точности требует
проведения дополнительных вычислений,
что увеличивает затраты машинного
времени.
ЗАМЕЧАНИЕ.
Необходимо отметить, что одношаговые
методы требуют для вычисления последующего
значения функции знание лишь одной
предыдущей точки разложения. Это
обеспечивает методам дополнительную
простоту, и, главное, позволяет без
особых трудностей изменять шаг расчета
в соответствии с величиной оцененной
погрешности.
4.5.3
Многошаговые методы численного
интегрирования Д/У
При
использовании многошаговых методов
для вычисления значения xk+1
используется информация о нескольких
вычисленных предварительно значениях
x(tk), x(tk-1),
x(tk-p).
Вспомним
постановку задачи интегрирования:
требуется вычислить функцию x(t)
при заданном дифференциальном
уравнении вида:
d
-
F(x.
t, v)
Многошаговые
методы используют различные способы
интерполяции функции x(t)
или заданной в аналитическом или
табличном виде производной F(x,t,v).
Предположим,
что найдено точное решение дифференциального
уравнения, т.е. некоторая функция
f(t)-x(t),
удовлетворяющая уравнению, т.е.
обращающая его втождество:
d
-
F(f
(t), t, v)
При
этом, очевидно, что правая часть уравнения
есть функция только времени, которую
обозначим через O(t),
т.е.
dx{t)
-
<*t)
dt
Заменим
функцию O(t)
некоторым интерполяционным
многочленом, например в виде степенного
ряда P(t)
в окрестности точки tk.
Используем для формирования
интерполирующего полинома схему
Ньютона с произвольно расположенными
узлами.
Пусть
интерполирующий полином P(t)
имеет степень n с
узлами интерполяции to,
t1,
..., ti, ..., tj,
..., tn.
В узлах полином равен интерполируемой
функции Ф (tk), т.е. Ф (tk)
- P(t\)
для всех
k - 0, 1, ..., п. Введем понятие
разделенной разности первого порядка
в виде:
р(>,)-р{М
.
tj
)-
<i
-
<j
По
аналогии определим разделенные разности
более высоких порядков:
t
I A
-
l
183
Pit,
to
)=
Л
I
t m
t -10
Pt,
1
t.
)=
t
Л и
т.д.
Тогда,
выразив из первого соотношения
P(t),
из
второго
— P(t,tci)
и
т.д., получим:
P(t)
=
P(i0)+P(t,
to)-(t-to)
Pft P P(t
^
<t
i
Физический
смысл разделенных разностей эквивалентен
приближенному значению производных
функции
P(t)
в
точке
и.
Предположим далее, что точка
и
подвижна, а отсчет времени производим
от некоторой точки
t0,
тогда:
ft Pft ,N
(
,
'o
)
=
P('o.
4)
+
( ■
-
t)
•
(t
i)
Т.к.
функция
P(t)
есть
многочлен степени n,
то
можно показать, что первая разделенная
разность есть многочлен
(П-1 )-0v\
степени,
вторая, соответственно, — степени
(П-2)
и т.д. Таким образом, n-ая
разделенная разность есть полином
нулевой степени, a
(n+1)
—
нуль. Таким образом, цепочка разделенных
разностей ограничена, при этом можно
осуществить последовательную
подстановку значений разделенных
разностей более высоких порядков в
функцию
P(t),
что
приведет к выражению:
P
(
' ) = P('o
)
+ ( I
-
'o
)• '1
) + ( I
-
'o
№
- '1 )•
P
('o' A
f2
)+
"» +
(t
-
'o
)(t
-
'1
Xt
-
tn-i
)•
P('o,
Л
- Л n
)
Таким
образом, многочлен
P(t)
выражается
через совокупность разделенных разностей
в узлах
t0,
t1...tn.
Величины
разделенных разностей можно вычислить
пореккурентным соотношениям,
приведенным выше. Необходимо отметить,
что, т.к. разделенные разности вычисляются
по значениям полинома в узлах интерполяции,
то они могут быть вычислены и через
значения функции
O(t)
в
точках
t0,
11...tn.
Вернемся
вновь к решению дифференциального
уравнения вида:
М
)
= 0 (
t ) dt
w
Представим
O(t)
интерполяционным
полиномом степени
P(t)
в
окрестности точки
tn.
Будем
считать, что значения
O(t)
в
точках
tn,
tn
-1,
tn-2,
tn-3
известны.
Тогда
#
) = #n
)
+ (t
-
tn
}• .
tn-1
)
+ (t
-
tn
Л
-
t
n
-1
}• #n
.
t
n-1.
t
n-2
) +
+
(t - tn Xt -
tn-1 )(t - tn_2 )
• <$>{tn
, tn_1, tn_2, )
Ограничимся
записанными членами, т.к. они определяют
четвертый порядок точности приближения.
В соответствии с видом дифференциального
уравнения, величина
x(tn+1)
определяется
в виде:
tn+l
x(tn+1
)
=
x(tn)+
j® с
)dt
n
Подставим
0(t)
в
последнеевыражение и проинтегрируем
его от
tn
до
tn+1.
184)-P('
0.Л)
J(t
- tn
Ж л ,
tn 1
)dt
tn
Представим:
t—j,
•П+1 'n+1r 1
\{t
-
tn
Xt
-
tn-1
)®('n ,
tn-1,
tn-2 )dt
=
J
l(t
-
tn
)2
+
hn_1
(t -
tn
)J- 4>{tn ,
tn-1,
'n-2
)dt
xtal
)
=
xn
+
i
=
xn
+
'n+1
)
d
t
+
j
f r
-
t
n
Ж
Л
.
tn-1
)dt
+
jfr-tn)(t-tn-1
Жл
,'n-1.tn-2)d'
+
+
J
(t
-
tn
Ut -
tn_1
)(t -
tn_2
)0(tn
,
tn 1,
tn_2
,
tn_3
)dt
tn
Будем
обозначать h
n
= tn
+1 - tn.
Рассмотрим каждый интеграл
вотдельности:
•П+1
jo(tn
d =
o
(
t
„
) . hn
(t
-
tn
h:
n
,
tn-1
) = ~T
,
tn-1
)
(tzt
n
l
+ h
('-K):
2
#
n
.
'n-1.
'n-2
)
hn
j h2n
•
hn-
#
n
.
t
n -1.
'п-
2 ) =
h
2
6
.(2hn
+
3hnhn_1
)-0(tn
,
tn_1,
tn_2
)
Аналогично
можно показать, что:
n+1
J
(t
-
tn
Xt -
tn-1
)(t -
tn-2
Ж
Л
, tn-1,
tn-2
,
tn-3
d
12
•
(3hn2
+
8hnhn_1
+
4hnhn_2
+
6hn2_1
+
6hn_1hn_2
)•
0(tn,
tn_1,
tn_2,
л
з)
Таким
образом, получаем формулу для нахождения
n + 1 точки с помощью
многошагового метода Адамса 4-го
порядка:
xn
+ 1
-x„+ hn
<
t
n
)+
-0 (tn,
tn_1)+
л
( 2
h
n
+
3hn_1
)-0(tn,
tn_1,
tn_2)
+
2
6
h
2 2
+
t^.(3h2
+
8hnhn
1
+
4hnhn
2
+
6hn21
+
6hI1
h
2
W
tV,t„
—t„
t„
з)
12
V
n n n-1 n n-2 n-1 n-1 n-2/
V
n' n—1?
n
—2?
n-3/
Таким
образом, для решения дифференциального
уравнения численным методом Адамса
необходимо знать величины разделенных
разностей вплоть до 3-его порядка, т.е.
необходимо предварительное определение
4-х точек, в которых функция O(t)
известна. Таким образом, для
реализации метода Адамса необходимо
предварительно вычислить значения,
хотя бы приближенные в точках tn,
tn-1,
tn-2,
tn-3.
К
185
Это
можно осуществить, например, предварительно
проинтегрировав дифференциальное
уравнение каким-либо одношаговым
методом, например, Рунге-Кутта или
Эйлера. Формулы, полученные для
произвольного расположения узлов
интерполяции, достаточно громоздки.
Более
часто используют формулы для равноотстоящих
значений моментов времени
'n,
при этом
разделенные разности заменяют конечными
по формуле:
АрФ
= p
\Mt
.,t
1,
,t
)
n
f£ \ rf '
n
-1
' ' n
-
p
/
При
этом
5 3
xn+1=
n
+
Ьф„п
+
2 ДФ + h3
-
а2ф„п
+ 8 h4
•
а3Фп
МетодуАдамса
присущ существенный недостаток,
состоящий в том, что при изменении шага
интегрирования с целью построения
более быстродействующих программ,
требуется произвести перерасчет
нескольких последних точек для того
чтобы использовать полученные результаты
в интерполяционной формуле.
Метод
Адамса
Система
дифференциальных уравнений, записанных
в форме Коши в явном виде:
dx
=
F
(x, t, v) dt
где
x
— вектор переменных состояния,
т.е. искомые функции времени. Предположим,
что найдено точное решение дифференциального
уравнения, т.е. некоторая функция f(t)
= x(t),
удовлетворяющая уравнению, т.е.
обращающая его в тождество:
ddx=F
(f (t \
t,
v) .
При
этом, очевидно, что правая часть уравнения
есть функция только времени, которую
обозначим через O(t), т.е.:
(dx
=
*<t)
Заменим
функцию O(t)
некоторым интерполяционным
многочленом P(t).
Пусть известны значения функции
O(t)
в моменты времени tn,
tn-1,
tn-1,
tn-3.
В этом случае (согласно теореме
о существовании и единственности
интерполяционного полинома) можно
построить полином 3-ей степени,
значения которого в узлах tn,
tn-1,
tn-1,
tn-3
совпадают со значением Q(t).
Используем
для формирования интерполирующего
полинома схему Ньютона с произвольно
расположенными узлами. Введем понятие
разделенных разностей для подвижного
узла интерполяции, который обозначим
через t:
AP(t)
= Л
— разделенная разность 1-го порядка
(полином 2-ой степени)
t
-
1n
Pit)-Pjtn
)
_
P
{tn )-p('n
-1)
„2>
/ч API
')-AP(t) f^T Г-1
> .
A
Pi')
=
—л л
= n n
—n
=1 разделенная
разность 2-го
'
-
'n 1 '
-
'n 1
порядка
(полином 1-ой степени)
186p
(t)_
p
(t
)
•П+1 tn+1
=
J
A2
P(tn
Xt
-
tn
)2
dt
+
j
A2P(tn
Xt
-
tn
K
-
d
t =
A2P(tn)
3
+
h
^
^
1
A3P{t)
=
_ _ _
разделенная разность 3-го порядка
(полином нулевой
t
- U
степени).
Тогда,
выразив из первого соотношения P(t),
из второго _ AP(t),
из третьего _ A2P(t),
получим:
P{t
)
= P{tn
)+AP(t\t -
tn)
AP(t)
= A2P{t
)(t -
tn_1
)+AP(tn)
A2P{t)
= A3Pfo
ft
-
tn-2 ) + A2PЛ)
Последовательной
подстановкой определим P(t):
P(t)
=
P(tn)
+
[A2P(t)(t
-
tn_1)+AP(tn
)](t - tn) =
=
P
(t n )+AP (tn
Xt - tn)+
[a3 P
(tn
)(t -
tn
_
2)+A2P
(t n )]•
(t-
tn
\t -
tn
_1) =
=
P(t„)+AP(tn
Xt -
tn)+A2P(tn
Xt -
tn
Xt -
tn_
1
)+A3P(tn
Xt -
tn
Xt -
tn_
1
Xt
-
tn_2)
Данный
интерполяционный многочлен определяет
4-ый порядок точности приближения. В
соответствии с видом дифференциального
уравнения решение в n + 1 точке
определяется точным соотношением:
x(tn+1
)=
x(tn)+
J®(t
)dt
tn
При
замене O(t)
интерполяционным полиномом по
формуле, приведенной выше:
tn+1 *n+1 *n+1
Х
1) =
xn+1
=
xn
+
J
P
i
'„
)dt
+
J
AP
('
n
)(t
-
1
„ )dt
+
J
A2
P(tn
)(t
-
'n
)(t
-
'n_1
)dt
+
+
J
A3
P
(tn
tn
)(t -
лп.
1 Xt
-
tn-2
)
Будем
искать каждый интеграл в отдельности.
При этом примем, что hn=tn+1
- tn
hn-1
tn
'п-1
, hn-2
tn-1 tn-2:
(n+1
JP{tn
)dt =
P{tn
)hn
h
■
\лp{tn
Xt
-
tn
)dt =
AP{tn)
2:
•П+1 tn+1
J
A2P(tn
)(t -
tn
Xt
-
tn 1
)dt
=
J
A2P(tn
)(t -
tn
Xt
-
tn
+
hn_1
)dt =
•ПA^Pit) AP2
(t
)
tn
tn
tn
tn
'n
187
JA3 P(tn )(' - tn X* - tn_1 )(' - 'n-2 )dt =A3 Pfo )• 1 2 [3hn2 + 8hnhn_1 + 4hA_2 + 6hn^_1 + 6hn_1hn_2 ]
tn
Формулы, полученные для произвольного расположения узлов интерполяции, достаточно громоздки. Более часто используют формулы для равноотстоящих значений моментов времени tn, при этом разделенные разности заменяют конечными по формуле:
АрРп = pWP{tn)
При этом
h2 5 3
хи+] = г + h Pn '-2 — AP . +|П— h -A2Pn + 8 h4 -A3Pn
n+1 n n^nlZ nO n
4.5.4 Методы прогноза и коррекции
В методах прогноза и коррекции для вычисления положения новой точки xk+1 используется информация о ранее полученных точках, однако для увеличения скорости сходимости метода после предварительного определения положения новой точки xk+1 осуществляется коррекция результата. Для этого применяются две формулы — прогноза и коррекции. Принципиально алгоритмы всех методов прогноза и коррекции одинаковы, отличия состоят лишь в формулах, по которым вычисляется прогнозируемое и корректируемое значения нового приближения.
Рассмотрим алгоритмы методов.
По какому-либо из одношаговых методов определяется достаточное количество точек "разгонки" метода, т.е. приближенного значения xk, Xk.1> xk-2,..., xk-p и т.д., в зависимости от порядка применяемого метода.
По формуле прогноза определяют значение xk+1 np=x(tk+1).
По исходному уравнению определяют величину производной F(tk+1, xk+"p, v).
Проводят одну или несколько (j) итераций с целью уточнения xk+1Kop, при этом оценивается норма вектора производных (точнее их разности) и сравнивается с заданным заранее приближением, т.е. величиной погрешности s:
F {tk + 1 , , v)-F( t k x л , v|<8
Когда значение производной вычислено с достаточной точностью, его используют для вычисления точного значения xk+1Kop.
Осуществляют переход к новому значению времени tk+2.
Простейшим из методов прогноза и коррекции является модифицированный метод Эйлера, в котором прогноз осуществляется в соответствии с одношаговым методом Эйлера, а коррекция — по модифицированному методу Эйлера в виде:
Ч + 1 = x k + h • F (x k , f k >v)
x -
= =xXK++2h •- № kkt kv V)+I FxgtfF, t,k+1, V)J
Необходимоотметить, что в этом случае полученная точка xk+11,Kop тоженеявляет- ся достаточно точной, т.к. нет гарантий того, что полусумма производных достаточно близко аппроксимирует реальный ход кривой. Применим теперь итерационную процедуру вида:
188
J+1Kop
_ и.кор <
xk+
1
xk+
1
- 1
.
Если
погрешность уменьшается с ростом
количества итераций, то можно
утверждать,
что процесс сойдется и
будет достигнута большая точность
вычисления xk+i.
Будем
опускать обозначение кор., т.к. ясно,
что в дальнейшем пойдет речь о
формуле
коррекции, т.к. прогноз
выполнен один раз. Оценим условия
сходимости итераций:
x'J+l.KOP х-
,kop
h г / ч , М
h
k+i k+i
=
2
•
i
[F
\{x
'.
h
:v /)
+
F
(xk+lrHkk-l-.i'v
)/j --
2
• [F
(xxk. \ v )
+F
(xk;1.
Ц
+
1. v)]
=
h
r F x л л '-i M h dF
=
|
?F
(xk+i. tk+i.
v)
+
F
(xk;i.
tk+i.
v )
] = h
•
|F
•
[xk+i
-
xk;1
]
xJ+i
-
x
J ^h
•
М
- \
х
J
-J_i1
хk
+ i
x
Ak
+ i -
2
M
х
■
х
■
h
2 h3
+
h
•Fi
x
k.
f
k.v)
+ ■
Л
tk k+1
-h
•
F
(
x
k
.tk
.
'
)+—2
•
F
'
(X
k
.
gk
.'
) + —
•
F
(
x
k .42.'
)
где
h
2 h
з
x
к T P
xk
+ | \ F x, tk,
v ) + F
i,
tk
+
i , v) ]
Будем
применять ее несколько раз, каждый раз
оценивая погрешность:
где берем
в средней точке xk+i, xk;i.
dx
Будем
предполагать, что производная функции
< M, т.е. ограничена,
тогда:
dx
i
+i
-г h
Ml ,
л
Тогда,
очевидно, если —< i, то
разница между значениями
x
в процессе коррекции
будет
уменьшаться с ростом числа коррекций
и можно ожидать, что при большом j
она станет меньше s.
Т.е.
если h<2/M,
то процесс будет сходиться, причем
тем быстрей, чем меньше
h.
Рассмотрим
вопрос о величине ошибки, возникающей
при использовании методов
прогноза-коррекции.
x(t)=
xk +(t -
tk
)•
F(xk,tk,v)+*
F \ x
k
,
t
k
g v .
f\xk,tk,v)
+ ...
+
h«F
i
x
k.
f
k.v
) + —2 •
F
(x
k.
f
k.v
)+ — g
F
(xk. v
)
где
h -1 - tk
h3
Xk+1
-
Xk-1
=
2h
•ixk.'k.v)+
—
• F"(xk.
s.v)
6
где
h
-1
-
h+1
89
Первые
два слагаемых представляют собой
собственно формулу прогноза, а третье
слагаемое — ошибка метода. Итерационная
формула коррекции:
=
xk
+ А •
[F
( x
■
f
k
•
v
)
+ F
(xk+1,
fk+1.
v)]
Аналогично
предыдущему можно показать, что ошибка
равна:
-
у •
F
"
(
x
k
,
Л ,v)
Таким
образом после проведения j
+1 итерации коррекции суммарная
максимальная ошибка составляет:
у
-
F
{
x
k
,
V
)
+ у
•
F
(
x
k
,
Л, V
)=-
xk+1
+
xk
+ !
Если
предположить, что 3-й производные близки
к постоянству:
F"
{xk,
t, v )= const
то:
x
j ;
-
-
*
+
1
-
h3
•
А •
F
(xk,
А
v)
12 -
где tM
<0<tk+i
Т.к.
погрешность формул коррекции s«
h_.
F" (xk,ц,v),
то, очевидно, ее можно вычислить,
зная xk+1
и xk+/+1:
5
Таким
образом, метод прогноза и коррекции
второго порядка позволяет оценить
ошибку действий путем сравнения значений
исходной и скорректированной величин
x.
Аналогичные
выкладки можно сделать и для методов
более высоких порядков. Эта оценка на
каждом шаге, подобно методам многошаговым,
дает возможность строить программы
с изменяемым шагом. Впрочем, при
"разгонке" метода (см. формулы
прогноза), можно оценить F',
и следовательно M и
выбрать T&2/M. Тогда, если
после первой коррекции ошибки (xk+/+1
-
xk+1)<s/5,
можно взять удвоенный шаг равный
2h. Если ошибка больше 5s,
необходимо шаг уменьшить в два
раза. И, наконец, в третьем случае
h=const.
Вопрос
устойчивости метода
Устойчивость
— способность устранять положение
ошибки.
Идеальным
случаем является такой, когда после
большого числа итераций:
h
=
xk
+
7
[
F
(
x
k
,
t
k
,
v
) + F
( C А
I
k
,
v
) ]
Т.е.
метод сошелся к некоторой точке xk+1c°,
которая, возможно, и не равна точному
значению xk+1,
для которого
xj
+ 1
-
x
190
яИяИНИеусгойчивым,
то -kj+±i
k+— растет с ростом
к.
xk+i
Можно
доказать (или показать), что методы
прогноза-коррекции 2-го порядка
являются
по крайней мере относительно
устойчивыми для любых реально используемых
в электронике
нелинейных функций
F, т.е. его использование
не приводит к расходимости.
Одним
из распространенных методов прогноза
и коррекции является
методХемминга.
ЗАМЕЧАНИЕ.
Методы прогноза и коррекции оказываются
более устойчивыми при ин-
тегрировании
сложных зависимостей, особенно с большим
разбросом постоянных времени
параметров
схем. В некоторых случаях методы прогноза
и коррекции требуют меньших за-
трат
времени и объема памяти для реализации
программы.
4.5.5
Неявные методы решения Д/У
Существенные
преимущества при расчете реальных
электронных схем имеют неявные
методы
численного интегрирования, которые
позволяют облегчить решение задачи
решения
д/у при значительном разбросе
постоянных времени, что характерно для
большинства
электронных схем.
Рассмотрим
выражение для
(k+i)
—
ойточкимодифицированного методаЭйлера:
x
r +
1 = x
k +h
-
Ил>xk>
v)+f
(t"xk
+
i,v)]+ek
При
этом можно говорить об относительной
и абсолютной устойчивости метода в
смыс-
x
x"
ле:
если xk+i-xk+im
уменьшается до нуля при любом k
и
-k±i
—
остается постоянным
xk
+ i
для
любого к.
«k
+ i =
xk
+2-(F(xk,
fk>v)+F
(xk + i>t
k +1 ))
Здесь
в методе Эйлера значение Xk+i
в правой части вычислялось, например,
простым методом Эйлера, а затем по нему
уточнялось значение xk+i
в левой части. Подойдем к решению
задачи с несколько других позиций.
Рассмотрим полученное выражение как
алгебраическое уравнение относительно
xk+i
и будем его решать, например методом
Ньютона или методом последовательных
приближений. Тогда, через определенное
количество итераций можно получить
точное значение xk+i.
Можно
предложить неявный метод 2-го порядка
(двухшаговый), выраженный итерационной
формулой Шихмана:
__
1 4 2
f, ч
xk+1
_ з xk-1
+ з ' xk
+
з ' h
'
F
vxk+1,
tk+1,v
/
Необходимость
использовать методы решения алгебраических
уравнений на каждом шаге интегрирования
дифференциальных уравнений увеличивает,
казалось бы, время счета при использовании
неявных методов. Однако для более точной
оценки необходимо учитывать полное
время, затрачиваемое на все шаги расчета,
а также на оценку погрешности. Неявные
методы позволяют легко создавать
программы с автоматической коррекцией
шага интегрирования, а также учитывать
при решении появление в системе
дифференциальных уравнений одного или
нескольких алгебраических уравнений,
также записанных в неявном виде.
191
Сравнение
методов
Достоинства |
Недостатки |
1. Метод Рунге-Кутта |
|
Можно помнить? решения можно изменять шаг |
необходимо произвести ряд вычислений во внутренних точках трудно оценить погрешность |
2. Многошаговые |
|
Гораздо более высокая точность (меньшая ошибка на каждом шаге) |
Трудно изменять шаг необходима "разгонка" метода |
3. Прогноза и коррекции |
|
Хорошо оценивается ошибка и делается вывод об уменьшении шага |
Требуется "разгонка" при изменении шага требует применения метода Рунге-Кутта |
4. Неявные |
|
Можно решать системы жестких уравнений хорошая сходимость (устойчивость) метода; легко изменять шаг; осуществляется переход к решению алгебраических уравнений |
Требуется "разгонка" |
4.5.6 Специальные алгоритмы анализа переходных процессов
в нелинейных схемах
Нелинейная схема содержит хотя бы один нелинейный элемент.
При анализе переходных процессов в нелинейных схемах нельзя использовать принцип наложения, который предоставляет возможность рассчитывать процессы в виде суперпозиции сигналов от разных источников. Таким образом, становится невозможным рассчитывать переходные процессы с помощью интегралов Дюамеля, наложения, классическим и операторным методом анализа переходных процессов.
При расчете переходных процессов удается воспользоваться лишь законами Кирхгофа, при этом вольтамперные характеристики нелинейных элементов могут быть заданы либо в графической, либо в табличной форме, или описаны аналитическим выражением. При этом предполагается, что нелинейный элемент является безынерционным, или его можно представить безинерционным нелинейным звеном совместно с инерционной линейной частью. Методы анализа переходных процессов в нелинейных схемах классифицируются:
по способу решения нелинейных дифференциальных уравнений на графоаналитические и численные;
по характеру величины, для которой производится расчет - на методы для мгновенных значений, методы для огибающих первых гармоник, методы для медленно меняющихся амплитуд.
192
Дифференциальные уравнения для нелинейных схем составляются по законам Кирхго- фа. Представляется удобным составлять дифференциальные уравнения для каждого реактив- ного элемента - индуктивности или емкости в следующем виде:
«du fi , diT
IC = C — u, = L
C dt • L dt
если они линеины, и в виде:
C
dQ dV
u
dt dt
если последние нелинейны.
При этом система дифференциальных уравнений для схемы n-oro порядка преобразует- ся к виду:
dd - f1 (л , У 2, -У п л)
Ф 2 dt
f2 (У1, У 2 5 - У п > ')
£Уп
dt fn (У 15 У2'-У, „ t)
где в левой части вынесены производные функций, а в правой — выражения для функций через параметры схемы, частично нелинейные, и сами функции, т.е. токи и напряжения.
Нахождение переходного процесса есть решение задачи Коши, которая формулируется следующим образом: требуется найти решение системы n дифференциальных уравнений первого порядка на заданном интервале времени (to...tk), если известны значения всех переменных в одной точке, как правило, это точка — начало интервала интегрирования. Значения функций в начале интервала определяются, как несложно догадаться, из независимых начальных условий.
Основные виды нелинейностей, характерных для электронной техники, были рассмотрены в разделе i настоящего конспекта, касающегося моделей компонентов электронных схем. Численные методы решения систем линейных и нелинейных дифференциальных уравнений рассматривались в соответствующем разделе курса математическое моделирование. Графоаналитические методы при современном уровне развития пакетов программ схемотехнического анализа не являются актуальными.
Нас будут интересовать лишь методы, позволяющие в той или иной степени облегчить решение системы нелинейных дифференциальных уравнений, а именно:
либо упростить алгоритм решения, сведя задачу на каждом шаге к анализу по постоянному току, что позволяет использовать ранее рассмотренный математический аппарат матричных методов;
либо пренебречь при анализе быстрыми процессами (с малыми постоянными времени), происходящими при коммутации ключевых элементов, и выявлять лишь динамику постоянной составляющей интересующей переменной состояния, усредняя значения производных переменных состояния за интервалы проводимости ключевого элемента (при этом неизбежна потеря информации о поведении переменной состояния внутри каждого интервала коммутации). Такой метод (усреднения в пространстве состояний) применяется для
93
