
- •Содержание 2
- •Введение. 136
- •2. Введение
- •1. Основные понятия
- •1.1 Моделирование. Основные понятия.
- •1.1.1 Системный анализ и моделирование
- •1.1.2 Концептуальные модели.
- •1.1.3 Термины и определения
- •1.1.4 Формализация и алгоритмизация процессов.
- •1.2 Математическое моделирование
- •1.2.1 Классификация математических моделей.
- •Классификация математических моделей на основе особенностей применяемого математического аппарата
- •1.2.2 Основной принцип классификации математических моделей
- •1.2.3 Программирование модели
- •1.2.4 Испытание модели
- •1.2.5 Исследование свойств имитационной модели.
- •Эксплуатация имитационной модели.
- •Анализ результатов моделирования.
- •1.3 Виды анализа и расчета электронных схем
- •1.4 Модели элементов и схем
- •2. Модели компонентов электронных схем
- •2.1 Классификация моделей
- •2.2 Интерполяция и аппроксимация функций при создании моделей
- •2.2.1 Интерполяция функций
- •2.2.2 Аппроксимация функций
- •2.3 Модели основных электронных компонентов
- •2.3.1 Базовый набор элементов моделей
- •2.3.2 1.1 Резистор
- •1. Пассивные компоненты и их модели
- •2.3.3 1.2 Конденсатор
- •2.3.4 Реальные конденсаторы
- •2.3.5 Катушка индуктивности и дроссель
- •2.3.6 Реальная индуктивность
- •2.3.7 Модели полупроводниковых приборов
- •2.4 Модели аналоговых компонентов программы Micro-Cap
- •2.4.1 Общие сведения о моделях компонентов
- •2.4.2 Пассивные компоненты
- •2.4.3 Резистор (Resistor)
- •Разброс сопротивления при использовании Monte-Carlo
- •3. Матрично-векторные параметры схем
- •3.1 Основные законы электрических цепей в матричном виде
- •3.2 Метод контурных токов
- •3.3 Метод узловых потенциалов
- •3.4 Метод обобщенных ветвей
- •3.5 Статический анализ линейных и нелинейных схем
- •3.6 Гибридный анализ электронных схем
- •4. Методы анализа переходных процессов
- •4.1 Введение
- •4.2 Литература
- •4.3 Основные задачи анализа переходных процессов
- •4.4 Анализ переходных процессов в линейных цепях
- •4.5 Анализ переходных процессов в нелинейных схемах и численные методы интегрирования нелинейных ду
- •4.5.1 Общие сведения о численных методах решения систем дифференциальных
- •4.5.7 Сведение расчета переходных процессов в электронных цепях к расчету цепей по постоянному току
- •4.6 Анализ переходных процессов в цепях с периодической
- •4.6.3 Дискретное преобразование Лапласа и его основные свойства
- •9. Теорема дифференцирования по параметру
- •10. Теорема интегрирования по параметру
- •11. Теорема об умножении изображений (теорема свертывания в вещественной области).
- •4.6.4 Решение линейных разностных уравнений
- •4.7 Параметрические цепи
3.2 Метод контурных токов
Введем понятие вектора-столбца контурных токов I. Размер вектора [ст,1], он имеет вид:
I
I
I
I _
Элементы матрицы Г показывают, как &-ый контур входит в s-тую ветвь схемы. Очевидно, матрицу Г можно использовать для связи величин контурных токов с токами ветвей. Для этого необходимо выполнить умножение матрицы Г на вектор I. Для этого, очевидно, необходимо транспонировать матрицу Г, заменив индексы у элементов местами: [Гу 1 = [Г.. ]. Теперь матрица rt имеет размер [l, а], тогда можно осуществлять умножение:
I е =Г, • I
Последнее уравнение отображает зависимость l токов ветвей от а контурных токов. Выберем последние в качестве независимых переменных, т.е. будем искать контурные токи, протекающие, по определению, через хорды схемы. Рассмотрим уравнение по закону Ома в виде:
U = Ze • I е + Ee Подставим в это уравнение значение Ie, равное Tt-I. Получим:
Ue = Z е Tt • I + Ee Умножим последнее равенство на матрицу контуров Г слева. Получим:
Г-ие = Г - Z е .rt • I+ Г.Ев По второму закону Кирхгофа Г • Ue = 0, тогда введем соответствующие упрощения:
Г-Ze-rt = Z Г-Ее = - Е Л Z •I = Е Рассмотрим размерность полученных выражений:
[Ft ] = [l, 4 Ze =[l, l]
[Ze Tt] = [l,a] r = [ a , l ] л Z = [a,a]
Таким образом, матрица Z - квадратная матрица размера [a, а], которая получила название матрицы сопротивлений схемы:
Z =
Z-i Zi2
Z2 1 Z 22
Z
Z
2а
Za1 Z
Вектор Е имеет размерность:
Z
79
Г
= [а, l
]
Ee
=[l ,1]л
E
=
[o,1]
Вектор
E
-
вектор э.д.с. схемы.
Нахождение
Z
и
E
не
представляет проблем, т.к. все компоненты
этих матриц известны. Таким образом,
мы приходим к матричному уравнению
вида
Z
•
I
=
E,
соответствующему
а скалярных уравнений, решение которых
можно осуществить, обратив матрицу
Z:
I
=
Z-1
•
E
Таким
образом, число скалярных уравнений или
порядок векторного уравнения снижен
с 21 до с. Принципиальных трудностей при
решении уравнения нет.
На
практике, особенно при решении уравнений
для реальных электрических схем,
получил
большее распространение
метод узловых потенциалов в матричном
виде,
который в ряде
случаев более удобен.
Введем
понятие вектора-столбца потенциалов
схемы U.
Будем
отсчитывать потенциалы всех узлов
схемы от некоторого базисного узла,
который не охвачен ни одним сечением.
Тогда вектор-столбец узловых потенциалов
щ
U
и
имеет
размерность [v,
1],
равную числу узлов схемы без одного,
т.е. числу ребер дере-
ва.
Вспомним
структуру матрицы главных сечений П
[v,
1].
Элементы матрицы П определяют
сечения, на которых оканчиваются ветви
схемы. При этом число элементов матрицы,
отличных от 0 в каждом столбце, всегда
равно 2, т.к. это означает, что ветвь
соединяет два узла схемы. Исключения
составляют ветви, выходящие из базисного
узла, или в него входящие, т.к. для них
число отличных от 0 элементов в столбце
равно 1.
Таким
образом, напряжение на ветви можно
характеризовать разностью потенциалов
между узлами, причем если ветвь соединяет
узлы i
и
j,
то
напряжение равно Ue=Ui-U/;
если
ветвь выходит из базисного узла схемы,
то напряжение на ней равно потенциалу
другого узла. Поэтому вектор напряжений
на ветвях размерностью [l,
1]
можно определить в виде матричного
произведения матриц Пи U,
однако
при этом матрица П должна быть
предварительно транспонирована т.е.:
к
] , = ] .
При
этом размер матрицы nt=[1,v],
а
выражение для напряжений на ветвях
схемы имеет вид:
Ue
=П,
U
803.3 Метод узловых потенциалов
Вспомним
выражение для закона Ома для представления
ветвей в виде параллельно объединенного
источника тока и проводимости:
I
.
= Y
-
и . +
J0.
Подставляя
в указанное выражение значение Ue,
выраженное
через nt-U,
получим:
I. =
Y-nt-U+^.
Умножим
это уравнение на матрицу П слева:
П-1в
= П-Ye
Ut
•U +
П- ив.
По
первому закону Кирхгофа в матричном
виде:
П-1
в
= 0.
Проведем
переобозначения:
и-¥в
Ut
=
Y J
=
- n
j
Здесь
Y
—
квадратная матрица размером [у, у],
которая получила название матрицы
проводимости схемы, вектор J
—
вектор размера [у, 1], называющийся
вектором задающих токов схемы.
Умножим
полученное уравнение на Y-1
слева,
получим:
Y-U
=
J
или
U
=
Y"1
•
J
Последнее
соотношение реализует метод узловых
потенциалов в матричном виде.
Последние
соотношения позволяют провести расчет
схемы по методу узловых потенциалов,
однако, для получения результата
необходимо определить значения матриц
7 и J.
В
принципе, задача решается путем
двухкратного перемножения матриц П,
Ye
и
nt,
а
вектор задающих токов схемы J
определяется
путем умножения матрицы П на вектор
Je.
Однако
такое решение задачи весьма громоздко,
т.к. требует выполнения операций с
матрицами. Существует формализованный
способ построения матриц 7 и J,
который
вытекает из свойств матрицы. Покажем
этот способ, а затем докажем его.
Можно
утверждать, что если схема состоит
только из двухполюсников, то матрица
Y
диагонально
симметрична, т.е. для любых к и s,
принадлежащих
интервалу k,s
е[1,
у] справедливо соотношение: yks=ysk
(напомним,
что размер матрицы Y
-
[у,
у], что определяется числом уравнений
относительно узловых потенциалов,
равного числу сечений схемы на единицу
меньшего, чем число узлов).
Элемент
диагонали ykk
равен
сумме проводимости ветвей, пересекаемых
k-тым
сечением. При этомykk
называется собственной проводимостью
k-ro
сечения.
y
ks
—
сумма проводимости ветвей, общих для
k-ro
и
s-ro
сечений;
yks
называется
взаимной проводимостью k-oro
и
s-oro
сечений.
При
этом порядок составления матрицы
состоит в следующем:
заготавливается
квадратная таблица размером уху,
т.е. числом строк и столбцов, равным
количеству главных сечений. Поочередно
рассматриваются все ветви, входящие в
схему, и их проводимости вписываются
с соответствующим знаком в соответствующие
клетки в виде слагаемых. Проводимости
ветвей алгебраически суммируются с
теми элементами квадратной
81
матрицы,
которые расположены на пересечении
строк и столбцов, имеющих номер
пересе-
кающих данную ветвь главных
сечений. При этом знак составляющих
взаимной проводимости
определяется
взаимным расположением главных сечений.
Рассмотрим
пример. Допустим, в схеме имеются
A,
В,
C,
D
сечения.
Очередная ветвь проходит через сечения
A,
C, D,
на-
правления
которых изображены на рисунке 3.7:
(Можно
предположить, что рассматриваемая
ветвь является
хордой, т.к. через
ребро, по определению, проходит лишь
одно
Ри°.
37 сечение).
При
этом составляющие матрицы
Y,
соответствующие
указанной ветви, имеют вид:
Очевидно,
что если ветвь пересекает m
сечений,
то она вписывается в m
клеток
табли-
цы. Проводимость ребер дерева
вписывается в клетки матрицы только
один раз.
Вектор
задающих токов схемы J
—
вектор-столбец, &-тая компонента
которого равна ал-
гебраической
сумме токов, подтекающих к &-тому
сечению.
Причем знак «+» выбирается в случае,
если
ток ветви противоположен направлению
се-
чения, а знак«-», если направления
сечения и то-
ка совпадают.
Рассмотрим
пример, основанный на приве-
денной
выше скелетной схеме некоторой цепи
рис.
3.8:
В
соответствии с выбранным направлением
токов
и главных сечений, матрица 7имеет вид:
A B
j
3
+ j
4
+ j
8
C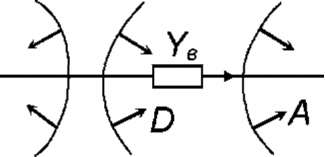
A B |
C |
D |
|
+ Ув 0 |
- У в |
+У в |
A |
0 0 |
0 |
0 |
B |
- Ув 0 |
+У в |
- У в |
C |
+У в 0 |
- У в |
+ Ув |
D |
A
D
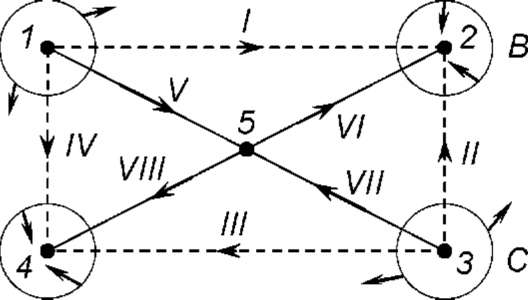
Рис. 3.8
C
D
Y =
У1 + Уа + У 5 |
У1 |
0 |
Уа |
A |
У1 |
У1 + У 2 + Уб |
У 2 |
0 |
B |
0 |
У2 |
У 2 + Уз + У 7 |
Уз |
C |
Уа |
0 |
Уз |
Уз + Уа + У 8 |
D |
Вектор задающих токов схемы:
Ji + Ja + j
J _ 1 + ' 2 + J 6
j 2 + 1 3 + 1 7
Докажем указанное правило составления матрицы проводимости и вектора задающих токов схемы.
82
По определению, матрица Y формируется в соответствии с соотношением:
Y = П- Ye Ut
Транспонируем обе части матрицы, используя предварительно сочетательный закон: Y =(n-Ye-nt )t =((n-Ye)-nt )t =n-(n-Ye)t =n-(Y. )t-nf
Так как матрица Ye диагонально симметрична и диагональна, следовательно Yet=Ye. При этом, очевидно, что результат перемножения матриц после их транспонирования не изменится, т.е. Yt=Y. Это означает, что матрица 7 диагонально симметрична. Т.е. первое свойство матрицы доказано.
Будем теперь обозначать элементы матрицы буквами 7iks.
ж ii ж 12 Ж1 k ж,
«21 Л 2 2 Ж2 k Ж2 l
п
% 1 % 2 Ж k Ж l
Kv2
Ж k Ж l
Диагональный элемент ykk матрицы Y получается умножением k-ой строки матрицы П на k-ый столбец матрицы Ye nt.
В свою очередь, k-ый столбец матрицы Yent получается умножением матрицы Ye на k-ый столбец матрицы nt. В результате элемент Ykk матрицы 7 можно определить в виде:
Укк = [k^P. П] ^столб^атр^ • ] = [kстр. П] Y • [Кстолб.]] = = [k Cmp.U]-Ye \k стр . П\ = [л k l ■ Л ... % ]• Ye 'кл л ... 1
(строка матрицы П равна столбцу транспонированной матрицы nt). Таким образом, можно записать, что:
ykk Уе1 n k 2 У в 2 ... КыУв1 J X[%1 Щ2 ... 1 =
Г2 2 2
!_ • Уе1 + • У в 2 + ... + - kl • У el J = Z • У si
i=1
Таким образом, проводимость k-то сечения определяется суммой проводимостей ветвей, входящих в это сечение со знаком (+), т.к. для всех ветвей входящих в сечение л = ±1, т.е. пш2=1. Для ветвей, которые в сечения не входят 7ik=0. Таким образом, второе свойство матрицы 7доказано.
Для недиагональных элементов матрицы Y — проводимостей между сечениями k и s (где ^s), по аналогии можно записать, что
Уь = % 2 > ... ]'Ye -[ns1, Ж s 2 , ... Л I
Т.к. матрица Ye диагональная, то последнее соотношение можно раскрыть в скалярном
виде:
83
I
Уъ
= -П
si
•
Ув1
+
Л
k
2
s
2
•
Уе
2 + -
+
-П
si
•
У
el
]
= Z
%
k
i л
si
'
У
i=1
Таким
образом, стало очевидным и третье
свойство матрицы Y:
Произведение
7iki-nsi
отлично
от нуля лишь для тех ветвей, которые
проходят одновре-
менно через два
сечения к и s,
причем
равно +1, если сечения направлены друг
относительно
друга одинаково, и
равно -1, если сечения направлены
встречно.
Полученные
соотношения также доказывают правильность
высказанного утверждения
для
составления матрицы Y
при
каноническом виде схемы с общим базисным
узлом. Т.е., если
сечения выбраны
одинаковым образом относительно узлов
схемы (например, все — наружу),
то
при определении взаимных проводимостей
сечений знак проводимостей ветвей
всегда от-
рицателен.
Рассмотрим
вопрос о векторе J.
По
определению, J
= -n.Je.
Для
k-той
компоненты векто-
ра:
l
i
k =
~ [П
к
i
'
пк
2 ]•
л
= •
}в1
+Пк2
-
je
2
+...
+ n
k i
•
jel
\
= ~Yj'Kki
•
J'ei
i=i
Поэтому
k-тая
компонента вектора J
равна
сумме задающих токов ветвей, причем
компо-
нента берется со знаком «-»,
если ток совпадает по направлению с
сечением схемы, и «+», ес-
ли ток
противоположен сечению схемы.
Сложность
матрицы Y
и
процесса ее составления существенно
определяется выбором
главных сечений
схемы. Спецификой радиоэлектронных
схем является то, что один из узлов
схемы
обычно принимают за базисный (нулевой),
которому присваивается нулевой
потенциал.
В реальных схемах
практически все узлы оказываются
связанными теми или иными проводи-
мостями
с нулевым. При этом процедура составления
матрицы Y
существенно
упрощается.
Главные сечения можно
выбрать охватывающими все узлы, кроме
базисного, причем каждое
главное
сечение охватывает только 1 узел. Дерево
схемы выбирается состоящим из
ветвей,
идущих от базисного ко всем
узлам схемы. При этом каждое сечение
характеризуется своим
потенциалом,
равным напряжению на соответствующем
ребре, т.е. ветви, соединяющей на-
званный
узел с базисным. Направления главных
сечений выбираются таким образом, чтобы
они
были направлены наружу.
В
соответствии с указанным выше
правилом,
собственные проводимости
сечений будут всегда
вычисляться
как арифметическая сумма проводи-
мостей
ветвей, исходящих из соответствующего
узла,
взятых со знаком плюс, а взаимные
прово-
димости сечений учитываются
со знаком минус,
т.к. сечения всегда
противоположно направлены.
Для
вектора задающих токов схемы правило
не
изменяется. Со знаком «-» учитываются
токи, вы-
текающие из сечений, со
знаком «+» — втекаю-
щие. Рассмотрим
пример, пусть задана схема,
изображенная
на рисунке 3.9:
При
указанном выборе дерева схемы матрица
проводимости схемы имеет вид:
84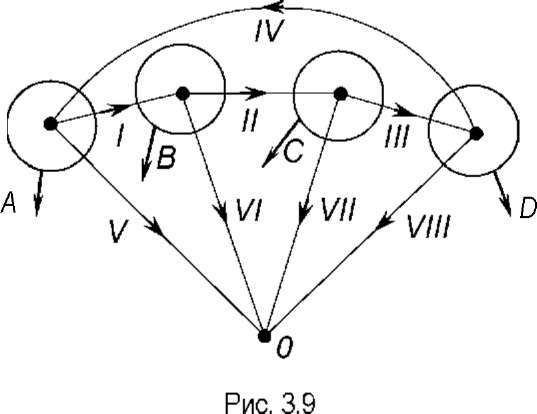
Нами
рассмотрены соотношения и правила
составления матрицы Y
для
схем, состоящих
только из двухполюсных
элементов. Однако реальные элементы
электронных цепей многопо-
люсные:
например, активные элементы: транзистор,
полевой транзистор, операционный уси-
литель,
тиристор, магнитосвязанные элементы
с потенциаль-
ным объединением
обмоток и т.д. Параметры этих элементов
также
могут быть представлены в матричном
описании, что не-
обходимо для расчета
схем матричными методами.
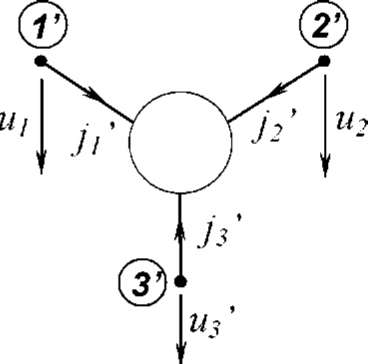
Рассмотрим
трехполюсник, выводы которого (узлы)
обо-
значены 1', 2', 3' (рис. 3.10). Выберем
направления токов внутрь
трехполюсника,
а узловые потенциалы отсчитываются от
неко-
торого внешнего узла, так что
все узлы трехполюсника равно-
значны,
и ни один из них не является базисным.
Тогда система
уравнений трехполюсника
в матричном виде имеет вид:
Рис.
3.10
Y
У1 + У 4 + У 5 |
- У1 |
0 |
- У4 |
- У1 |
У1 + У 2 + Уб |
- У 2 |
0 |
0 |
- У 2 |
У 2 + У3 + У 7 |
- У3 |
- У4 |
0 |
У3 |
У3 + У4 + У 8 |
Вектор задающих токов схемы:
j +
4 - J 5
J
1 ~ J2 ~ 6
J 2 ~ J 3 _ J 7
3
J 4
8
л |
|
У н' |
У12' У13' |
|
U1 |
J 2' |
= |
У 21 |
У 2 2' У 2 3 ' |
|
U2 |
|
|
У3 1' |
У 32' У33' |
|
U3 |
Можно записать ее более компактно в виде:
J' = YU '
Квадратная матрица Y' может быть рассмотрена как обобщенный параметр трехполюс- ного элемента. Все элементы матрицы имеют размерность проводимости, она называется матрицей проводимости трехполюсника.
Необходимо отметить, что матрица проводимости в указанном виде особенная. Линейно независимыми являются лишь 4 элемента матрицы из 9. Несложно показать [3], что в соответствии с законами Кирхгофа:
X уд' = 0 (k = 1,2,3); ]Г ysk' = 0 (s = 1,2,3)
s=l k=l
Необходимо также отметить, что матрица Y проводимости трехполюсника как правило, несимметрична относительно главной диагонали, так как большинство реальных трехполюс- ных элементов необратимы. При смене номеров узлов в матрице соответствующим образом меняются строки и столбцы матрицы.
85
Рис.
3.11
В
случае, если по каким-то причинам
известна лишь неособенная матрица
проводимости
трехполюсника, то
особенную можно сформировать на
основании приведенных выше уравне-
ний,
вытекающих из законов Кирхгофа:
Если
один из узлов матрицы подключен к
базисному, то можно сформировать
неособенную матрицу проводимости
трехполюсника Y'
путем
вычеркивания соответствующего столбца
и строки особенной матрицы. Например,
если трехполюсник подключен в соответствии
со схемой рис. 3.11, то соответствующие
уравнения имеют вид:
\j
2
= у21'"и1'+У
22 V
J
'
= Y
U '
а
матрица Y:
Y'=
У11
У12
У
2 1'
У11 У12 -
У
11-
У12
У2
1' У22
' -
У21'
У22
'
Ун'-У2
1' У12'
У22' Уц'+У21'+У
12'+
У22
Возникает
вопрос о формировании матрицы проводимости
схемы при наличии в ней трехполюсных
элементов. Рассмотрим следующий подход
к формированию. Вначале исключим
трехполюсные элементы из схемы и запишем
матрицу проводимости оставшейся части
схемы, состоящей теперь только из
двухполюсников. Для этого в схеме
выберем базисный узел; составим дерево
схемы и получим, таким образом, диагонально
симметричную матрицу проводимости.
Включение
трехполюсников изменит фактически
токи узлов (сечений) к которым подключены
элементы-трехполюсники. Пусть некоторые
узлы схемы p,
q и
г соединены с узлами 1', 2' и 3' трехполюсника,
соответственно. Если бы схема
трехполюсников не содержала, то
матричное уравнение, записанное в
соответствии с методом узловых
потенциалов:
J
= Y-U
означало
бы компактную запись уравнений вида:
г
V
J
\
= Z
У
1s
su
s=1
Л
= Z Уу
s
u
s
s=1
Теперь,
когда токи узловр, q
и
г изменились, для них можно записать
уравнения в виде:
86
s
u
s
jp
-
J
1
= S
Ур
8-1
V
Jq
-
J
2
' = Z
Уqs
U
s
8-1
V
Jr
-
J3
= Z yrs
u
s
s=1
Здесь
токи узлов jj',
j2',
Jз'
определяются равенствами, описывающими
трехполюсник в матричном виде:
'
i = Z
У
ik
ч
'
k
= 1
3
J
2
" Z
y
2
k
k = 1
3
J3
= Z
y3k''U,
k=1
Если
заменить потенциалы uj',
U2',
и из'
на эквивалентные Up,
Uq,
и Ur,
получим:
Jp
=
Z
yps •
Us +yn'Up + У12
' Uq + У13'
Ur
s=1
Jq
= Z У
qs
•
Us
+ У
21'
Up
+ У
22
Uq
+
У23
'
Ur
s=1
Jr
= Z
yrs
•
U
s
+
У
3 1
Ч
+
У3
2 '
U
q +
У3
3 '
U
r s=1
Таким
образом, вектор задающих токов Jдля
схемы, содержащей трехполюсники,
записывается аналогичным образом
соответствующему вектору для схемы,
трехполюсников не содержащих. Матрица
проводимости схемы меняется: к элементам
матрицы, записанной без учета
трехполюсников на пересечении строк
и столбцов с номерами узлов, соответствующих
точкам подключения трехполюсника
прибавляются соответствующие элементы
матрицы проводимости трехполюсника.
Если заменить номера узлов трехполюсника
1', 2' и 3' на номерар, q и r,
то остается лишь дописать
соответствующие элементы Y'
в матрицу проводимости Y
в виде слагаемых:
Г'=У
У11
У12
У13 Р
Если
один из узлов схемы соединен с базисным,
то этот узел не учитывается при
составлении матрицы проводимости
схемы Y, а соответствующие
элементы матрицы Y' не
включаются в таблицу в виде слагаемых.
Активные
элементы электронной техники: транзисторы,
операционные усилители, в эквивалентной
схеме могут быть представлены как
зависимые источники тока или напряжения,
отображающие их усилительные свойства.
Возникает вопрос о матричном описании
схем с такими элементами.
q
У
У
2
1
2
2
2
3
r
У
У
У
3
1
3
2
3
3
87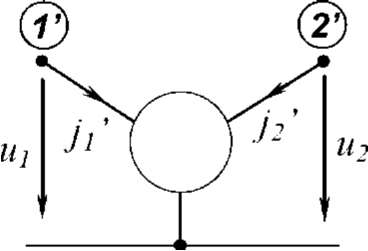
Во-первых,
будем рассматривать лишь зависимые
источники тока, управляемые напря-
жением,
т.к. этот вид зависимых источников
наиболее просто включается в матричное
описа-
ние (другие типы зависимых
источников; в принципе, могут быть
преобразованы в указанный,
либо
использованы при другом подходе к
описанию схем — в виде гибридных
матриц).
Во-вторых,
используем описанный выше подход, когда
вначале при составлении матри-
цы 7
все зависимые источники из схемы
исключены. При этом из оставшихся
двухполюсных
элементов образуется
диагонально симметричная матрица Y0,
для
которой справедливо соот-
ношение:
J
0
=
Y0
U
Здесь
J0
—
вектор задающих токов схемы, U
—
вектор узловых потенциалов.
Если
предположить, что имеется некоторый
зависи-
мый
источник тока, подключенный к узламp
и q
схемы,
а
его величина определяется
соотношением (рис. 3.12):
j
=
S-(Uk
-
Us)
jp
Л
yp
1=1
jq
i=1
Если
один из узлов, к которым подключен
источник тока, соединен с базисным
(например,
q),
то
в матрицу добавляются лишь два элемента
+S
и
-S,
расположенных
на од-
ной строке матрицы. Если
соединен с базисным один из управляющих
узлов источника, то ос-
таются два
элемента +S
и
-S,
расположенных
в одном столбце матрицы. Если источник
со-
единен с базисным узлом и
управляется напряжением, отсчитываемым
от базисного узла, то в
матрицу 7
дописывается лишь один коэффициент +S
или
-
S. 9+Е„
В
целом, в соответствии со сформулированным
выше
правилом для составления матрицы
проводимости Y
и
век-
тора-столбца задающих токов J,
если
направление зависи-
мого
источника тока совпадает с направлением
главного се- 1 " 1
R,
R 2
p —
q
jy
= S(Uk-Us)
Рис.
3.12
где
Uk,
Us
—
потенциалы узлов k
и
s
схемы,
a
S —
крутизна управления (А/В), то несложно
сообразить, что уравнения, описывающие
ток в сечениях, будут иметь вид (при
условленных положительных направлениях
см. рис. 3.2):
jp
-
(S
u
k
-
S.
Us)
=
X
y pi
u i
X
ypi-
Ui
+
S
U k
-
S.
Us
Jq
+
(S
•Uk
-
S
•Us)
=
X
yq
i
u
1
1=1
£
yq
r u -
S
U
k
+
S
U
Каждый
из зависимых источников тока, управляемых
напряжением, характеризуется записью
коэффициента S
в
четырех клетках матрицы:
|
+ S |
|
- S |
|
|
|
|
|
|
|
- S |
|
+ S |
|
|
|
|
|
|
затвор
с 2
s
k
s
p
q
Рис. 3.13
®
Л
с2,
2
=
j
®
v
Y4
=
R-
+R-
+
jaCc
чения
(а именно наружу), а потенциал узла
входит в управляющую характеристику
со знаком «+» (узлы p
и
к в приведенном примере), то управляющий
параметр (крутизна управления)
записывается в соответствующую
клетку матрицы со знаком «+». Если оба
этих условия не выполняются, то
крутизна управления также записывается
со знаком «+». Если выполняется лишь
одно из условий, то крутизна управления
записывается со знаком «-».
ПРИМЕР
Построить
матрицу проводимости схемы 7усилительного
каскада на полевом транзисторе с
общим стоком (рис. з.1з).
Рассмотрим
эквивалентную схему каскада по
переменному току (рис. 3.14).
Для
упрощения записи элементов матрицы
преобразуем схему, заменив, по возможно-
1
„Q 2 „с»
1
1 затвор" II
ш.
Тс,
исток
сток
у
и
® й"< О*
\R„
сти,
последовательно и параллельно
включенные элементы общими комплексными
проводи- мостями рис. 3.15.
SLL
©
Y
2
C
D -
-Ys
CZb
3
-с
Рис.
3.14
SU
©
to
п
Рис.
3.15
Yg
= 0; Y = joC,;
*2 — +
R
1
1
3U,
y
5 = j®C 2;
Y6
=
J-
6
R.
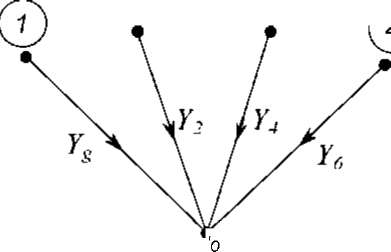
Схема
приведена к каноническому виду. Составим
дерево схемы в виде рис. 3.16. © ®
)>С1 |
- >С1 |
0 |
0 |
- j®C1 |
MC + Сзс + Сз„) +1 R1 |
- j & C s u |
0 |
0 |
- j&Csu - S |
m(C2 + C + С ) + - + - + S J V 2 CU 3U / TJ T-) |
- j ® C 2 |
0 |
0 |
» i r2 - > C 2 |
j&C + — 2 R |
Рис. 3.16
Без учета зависимого источника тока матрица Yo имеет вид:
12 3 4
Y , + Y 1 |
- Y1 |
0 |
0 |
- Y 1 |
Y 1 + Y 2 + Y 3 |
- Y3 |
0 |
0 |
- Y3 |
Y3 +Y4+Y5 |
- Y5 |
0 |
0 |
- Y5 |
Y5 + Y6 |
89
Проводимость
передачи Y^
=
L
и
(причем ZnepH/Ynep);
в:
U
I
в
'ex Yh
Це,
^
Ym
1-вы
U
вых
• YH
_ Y
Полная
матрица проводимости Y:
1
2
YПР
~
"u _
K
u
•
Yh
Y1 |
- Y1 |
0 |
0 |
1 |
- Y1 |
Y1 + У2 + Y3 |
- Y3 |
0 |
2 |
0 |
- Y3 - S |
Y3 + Y4 + Y5 + S |
- Y5 |
3 |
0 |
0 |
- Y5 |
Y5 + Y6 |
4 |
3.3.1 Функции электронных схем
Метод узловых потенциалов позволяет рассчитать потенциалы всех узлов схемы, если задано входное воздействие, а также матрица проводимостей Yдля схемы. Но иногда надо знать не сами потенциалы узлов, а связь между сигналами на входе и выходе схемы, т.е. определить усилительную способность схемы при различной нагрузке и различных источниках входного сигнала. Такие характеристики являются функциями схем, которые могут быть определены по матрице проводимости без расчета режима работы всей схемы. Схему представим четырехполюсником, в котором выведены входные и выходные узлы. Отметим, что схема представляет собой усилитель, фильтр и т.п. (но не генератор), т.е. в ней отсутствуют независимые источники сигнала.
J Г
1 = YY • и
вых н в
Перечислим основные функции схем: Коэффициент передачи по напряжению Ku =
Коэффициент передачи по току Kt =
L
Сопротивление передачи Z
nep
U L
Входное сопротивление Zex =
1
Входная проводимость Yex =
L 1
' ex вх
Функции схем связаны между собой следующим образом:
U
1
пер
K± Y
K4
K
K 1
« U 11 вых K U • Yh
Y _ lex.
U
Z
K U • Y H
K
3
4
Y
U
r "ex
u
u
L
Z
1
Z
90
Д..=
M..
«4(-1yY+J
Вводятся
также понятия режимов холостого хода
(Yh=0)
и
короткого замыкания (Гк=да).
В случае работы схемы в режиме холостого
хода ее функции обозначаются с верхним
индексом <<0»(Ku°),
короткого
замыкания — с верхним индексом
«к»
(K/).
Пусть
схема представляет собой усилитель
или частотно-формирующий каскад, где
нет независимых источников сигнала.
Рассмотрим вопрос об определении
функций схемы через параметры матрицы
проводимости Y.
Согласно
методу узловых потенциалов:
U
= Y-1 • J
При
этом вектор задающих токов схемы имеет
2 компонента, соответствующих входному
и выходному токам схемы (рис. 3.17). В узел
«а» входной ток втекает, следовательно
он берется со знаком «+», выходной
ток вытекает из узла «Ь», следовательно
он берется со знаком «-». Узловые
напряжения в узлах «а» и
«Ь»
соответственно — Uex
и
ивых:
Ub
Предположим,
что матрица про-
водимости 7
имеет
следующий вид:
У11
У12
У1Л-
Y
=
У 21
У22 У2\
Y
г
I.
Yh
U
U
и
a
вых
e
x
Уу
1
У
v
У
v\
Рис.
3.17
Для
построения обратной матрицы Y
надо
найти алгебраические дополнения для
каждого элемента, разделить их на
определитель матрицы Y,
полученную
матрицу транспонировать:
Y-![]()
![]()
![]()
Дл |
А 2 1 |
|
А |
А |
А |
|
А 22 |
|
А |
А |
А |
АЛ А А
Aw А
Здесь Ау — определитель матрицы, полученной из исходной матрицы Y путем вычеркивания i-ой строки иу-ого столбца, умноженный на (-1)+':
Нас интересуют потенциалы входного (а) и выходного (Ь) узлов, поэтому полное матричное уравнение решать нет смысла. Надо рассмотреть 2 строки, соответствующих узлам «а» и «Ь»:
1
1
U а = Т • Z Аsa & s—1
= T ' Z A sb A s—1
Т.к. в векторе задающих токов J всего 2 ненулевых элемента, то
и
у
V
V
b
s
s
в Х
91
U
вых
д -iA
ab •
1вх
-
A
b
bb •
1
в ых / )
\'xAaa
ГАД
abb
U
вх_
A
aaA
bb
•
1
вх -
AbbaA
b
b
•
1вых
ЛАА
U
_
a
Ah •
1 -A
Abbb.
•
1
л aa
вых aa
ab вх aa
bb
AA
abU
ex
-
A A
aaU
вых
_ A
aAblb"
1
вых
-
А
afl
,
ba
•
1вых
Л
Ц
. „ А Aab
U
вх
A
A
a a
+\
(Aa
a
^
- A
^A
ь
ь)
/•
Y
н
Из
теории определителей известно, что:
А
Л.ь
-
А Л ,
b
_
А ,ьь
aa
bb a^ '
ba aa'bb
ивх
д aa1
вх
лЬа
1вых
u
вых
д ab
1
вх ЛЬЬ
1вых)
Эти
уравнения преобразуем так, чтобы
выделить интересующие нас параметры
1
вх
и 1
Для этого исключим их уравнений
1
вх.
U
вх_
IT
-(А
aa
^
1"х
- A
b
ba
•
1
вых
) \'
хА
ab
вычитаем
из
1
-го 2-е {
1 ab
u
в
х л aa
u
в
ы х ) л
еых-
Aia
Abb
ь
-
A
a bb
A
bb a
1
вых и ивых
связаны между собой через параметры
нагрузки: 1ebix_Uebix-YH.
Используем
это в последнем уравнении:
А
aЬUвх
A
a a
u
в
ы х
>
ивых
Y
H
(лaaльь
лaьльa>
Ц
в ы х & a
a +
(
K
a \
b
~
\ b
\
a
>
' Y
>
_
А
Aabuex л
K
U
А
где
Aaa,tb
—
двойное алгебраическое дополнение,
полученное из исходной матрицы путем
вычеркивания строк и столбцов с номерами
a
и
b
соответственно.
Ун
вкл. в матрицу Y
—
по формуле
KU0
Ун
не вкл. вматрицу Y
—
по формуле
KU
Таким
образом, функция схемы Ku
получилась
как результат матричных операций, не
связанных с расчетом схемы. Несложно
получить соотношения для режима
холостого хода:
Y
_
0 л K
°
_
Aab
u
А
и
короткого замыкания:
YH
л
л KK
_
0
Если
составить эквивалентную схему, включая
в нее
Yh,
то
мы должны рассчитать схему для режима
холостого хода (т.к. ток нагрузки
1н
уже учтен в матрице). Если
Yh
не
входит в матрицу проводимости, то
Ku
считается
по общей формуле.
л
92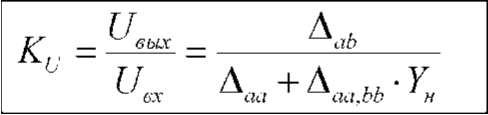
При
выполнении всех преобразований матриц
рекомендуется входной узел всегда
делать
первым, выходной — последним.
При этом подматрицы получаются проще.
Для
нахождения
Ki
рассмотрим
второе из исходных уравнений (для
Ueblx).
Замена
L
-
1
YH
ВКЛ.
В
матрицу Y — по формуле
Ктк,
при этом разрывается цепь
между
YH
и землей
YH
невкл. вматрицу Y —
поформуле К
Несложно
получить соотношения для режима
короткого замыкания:
А.
Yн
дает:
Т
Y
Л
л
Д
У
ab
J
Y
ab
к
К
А
bb
и
холостого хода:
Y.
=
0 К ; = 0
Все прочие функции схемы
выражаются через
Ku
и
Кт:
Y
=
1_вх_
1
вых
•
Ки
YTKU
ех
U
,
KI
•
UebL
Kr
Подставив
в выражение для Yex
выражения
для
Ku
и
К через определители, получаем:
YЛ
=
Yn
-
A
aab V
( А + Ун
•
A
bbb )
(
a
aa
+
Y
н
-A
aabtbb)-A
lib
*
Yh
a
+
Yh
-Abb
A
+
Y.
-A
aa,bb
1. Yh
ВКЛ.
В
матрицу Y
—
по формуле
YEX'
2. Yh
невкл. в матрицу Y —
по формуле
YsX
Получим
соотношения для режима короткого
замыкания:
и
холостого хода:
Y
f
aa,bb
Y.
=
0
=
л А.
В
результате матричных преобразований
размерности выходных величин должны
сохраняться. Для выражений
Ku
и
К размерности матриц числителя и
знаменателя одинаковы, для Yex
—
порядок матрицы числителя больше
порядка матрицы знаменателя.
Еще
одна функция проводимость передачи
Ynep:
у
^
пых
"ер
и
и
■У
вых
н
II..
К
и -У„
7
_ ^
чых
_ 1вых
_
К]
пер
/
1.-Y,
Y..
вых
У
bb
У
У
93
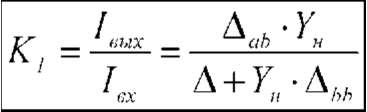
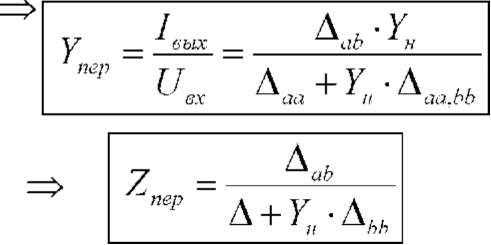
Для
нахождения Yebix
воспользуемся
следующим приемом: т.к. четырехполюсник
формально симметричен, то поменяем
(формально) индексы, соответствующие
входным и выходным узлам. При этом
вместо
Yh
будет
записана Ys:
Л
+ Yr
'А
aa
Д
■ +
YP
-А
a
a ,
bb
Как
правило, для реальн. источн. Rr-A0
или
Угл<».
Ун
вкл. в матрицу проводимости У, Уеыхсчит-ся
по формуле:
Y„„
=
Y.t
Рассмотрим
вычисление функций схем для каскада с
общим стоком (см. рис. 3.13, 3.14). Ранее для
него получили матрицу проводимости Y:
Y=
Любой
из элементов матрицы является комплексной
величиной, состоящей из активной и
реактивной компонент. Чтобы найти
функцию схемы в частотной области,
вначале надо записать каждый элемент
yks
через
значение параметров схемы. Проанализировав
выражение для требуемой функции схемы,
необходимо определить те подматрицы,
которые нужны для расчета. Например,
если рассчитывается
Ku,
a
Yh
включена
в состав матрицы, то нужны только Aab
и
Aaa.
Необходимо
записать выражения для вычисления
определителей, заведомо вычеркнув
строки и столбцы в матрице Y.
У11 |
У12 |
У 1 3 |
У 1 4 |
У 21 |
У22 |
У 2 3 |
У 2 4 |
У31 |
У 32 |
У 3 3 |
У 3 4 |
У 41 |
У 42 |
У 4 3 |
У 4 4 |
Y
j a Q |
- j® C |
0 |
0 |
- j®C |
/юС, + — + ■ Ri + j ® C G D + j ® C g s |
- j ® C G S |
0 |
0 |
- S - j ® C G S |
M C G S + C D S + C 2 > + 1 1 С + — + —2 + S |
- J ® C 2 |
0 |
0 |
- J ® C 2 |
/®C2 + — 2 L R« J |
Y
а — 1-ый узел; b — 4-ый узел.
* Yh может включаться и не включаться в матрицу проводимости в зависимости от искомой функции и используемых формул (см. выше).
|
У22 |
У23 |
У24 |
|
У 2 2 |
У 2 3 |
У 2 4 |
А = aa |
У32 |
У33 |
У 3 4 |
•(-1)2 = |
У 3 2 |
У 3 3 |
У 3 4 |
|
У42 |
У43 |
У 4 4 |
|
У 4 2 |
У 4 3 |
У 4 4 |
94
