
- •Содержание 2
- •Введение. 136
- •2. Введение
- •1. Основные понятия
- •1.1 Моделирование. Основные понятия.
- •1.1.1 Системный анализ и моделирование
- •1.1.2 Концептуальные модели.
- •1.1.3 Термины и определения
- •1.1.4 Формализация и алгоритмизация процессов.
- •1.2 Математическое моделирование
- •1.2.1 Классификация математических моделей.
- •Классификация математических моделей на основе особенностей применяемого математического аппарата
- •1.2.2 Основной принцип классификации математических моделей
- •1.2.3 Программирование модели
- •1.2.4 Испытание модели
- •1.2.5 Исследование свойств имитационной модели.
- •Эксплуатация имитационной модели.
- •Анализ результатов моделирования.
- •1.3 Виды анализа и расчета электронных схем
- •1.4 Модели элементов и схем
- •2. Модели компонентов электронных схем
- •2.1 Классификация моделей
- •2.2 Интерполяция и аппроксимация функций при создании моделей
- •2.2.1 Интерполяция функций
- •2.2.2 Аппроксимация функций
- •2.3 Модели основных электронных компонентов
- •2.3.1 Базовый набор элементов моделей
- •2.3.2 1.1 Резистор
- •1. Пассивные компоненты и их модели
- •2.3.3 1.2 Конденсатор
- •2.3.4 Реальные конденсаторы
- •2.3.5 Катушка индуктивности и дроссель
- •2.3.6 Реальная индуктивность
- •2.3.7 Модели полупроводниковых приборов
- •2.4 Модели аналоговых компонентов программы Micro-Cap
- •2.4.1 Общие сведения о моделях компонентов
- •2.4.2 Пассивные компоненты
- •2.4.3 Резистор (Resistor)
- •Разброс сопротивления при использовании Monte-Carlo
- •3. Матрично-векторные параметры схем
- •3.1 Основные законы электрических цепей в матричном виде
- •3.2 Метод контурных токов
- •3.3 Метод узловых потенциалов
- •3.4 Метод обобщенных ветвей
- •3.5 Статический анализ линейных и нелинейных схем
- •3.6 Гибридный анализ электронных схем
- •4. Методы анализа переходных процессов
- •4.1 Введение
- •4.2 Литература
- •4.3 Основные задачи анализа переходных процессов
- •4.4 Анализ переходных процессов в линейных цепях
- •4.5 Анализ переходных процессов в нелинейных схемах и численные методы интегрирования нелинейных ду
- •4.5.1 Общие сведения о численных методах решения систем дифференциальных
- •4.5.7 Сведение расчета переходных процессов в электронных цепях к расчету цепей по постоянному току
- •4.6 Анализ переходных процессов в цепях с периодической
- •4.6.3 Дискретное преобразование Лапласа и его основные свойства
- •9. Теорема дифференцирования по параметру
- •10. Теорема интегрирования по параметру
- •11. Теорема об умножении изображений (теорема свертывания в вещественной области).
- •4.6.4 Решение линейных разностных уравнений
- •4.7 Параметрические цепи
( U
т ВЫХ
IC2
-
S2
(
U
2
_ 1
C
2
R
2
* b2
(
I
C 2
R
2
Г )> . ..
In"
i_
e 2 C2 2 +2
(C2 2 f у
R-
H
I ~
ВЫХ
V У "c2~
*
' Ci
UBbIX
~
(
I
C i I
C
2
)RJH
f Pi
(E
n
~ (I
c i ~ I C 2
) R
h
-ICR )
Л
U
i
+ I
ciRi
+ bi{I
ciRi)
I
Ci
=
SiUi
-IciRi
+
bi(IciRi)2)x
i-e
V У
A P2
((ICi-IC2 )Rg-IC2R2 )
A
Ic2
= S2
(U2 -
Ic2R2
+
b2
(Ic2R2
)2
)X
i_
e
U2+Ic
2R2
+b2
(Ic 2R2
)2
V У
Ucm
~
En
Ueblx
U
3
m
-
En
Ueblx
RJCI
л
1
C
\
R
H у
R
U
U
С И 2
BbX
Ucm
=
f
(
l
a
)
U
3
T
=
ф (
7
С 1 ) U
C H 2
=f
{
I
C
2
) иЗИ
2
= ф (
7
С 2)
Ic
1
= S
Ui -
ICiRi
+
bi(lCiRi
)2
)x i-e
2
W i .
0 U
i +
I
C
i R +
b
{
I
C
R )
У
' P2
{UBL 1X-C2r2 ) Л
a Pi(
En
-Unbix
~^iRi)
Л
3.6.1
Формирование уравнений гибридного
резистивного 2п-полюсника
В
методах узловых потенциалов, контурных
токов, методе обобщенных ветвей в
качестве переменных и неизвестных в
уравнениях использовались физические
величины одного типа: в методе узловых
потенциалов и обобщенных ветвей —
напряжения, точнее узловые потенциалы
схемы, в методе контурных токов — токи
схемы. Зачастую более удобным оказывается
использование при составлении
уравнений электронных схем напряжений
и токов в отдельных элементах или точках
схемы. Составленные таким образом
уравнения называются
гибридными
уравнениями.
Удобство
использования гибридного анализа
состоит в том, что путем определенных
математических преобразований
удается проводить расчеты не только
обычных линейных схем, но и нелинейных,
в которые включаются положительные и
отрицательные нелинейные сопротивления,
зависимые источники напряжения и тока,
управляемые напряжением и током в том
числе нелинейные, реактивные компоненты:
конденсаторы и индуктивности. Гибридный
анализ оказывается особенно удобен,
если схема содержит незначительное
количество нелинейных компонентов, но
большой процент управляемых источников
и линейных компонентов.
Идея
гибридного анализа состоит в том, что
в исходной схеме осуществляется
выделение всех нелинейных элементов,
реактивных элементов, в результате
чего оставшуюся часть схемы, состоящую
из линейных активных резисторов,
независимых и зависимых линейных
источников напряжения и тока,
представляют в виде некоторого
2т-полюсника, все выделенные элементы
являются нагрузкой которого. Сточки
зрения физического смысла задачи все
проведенные операции являются
корректными, т.к. схема лишь разделяется
на две группы компо
1093.6 Гибридный анализ электронных схем
ванного
по таким правилам 2m-
полюсника
N
имеется mi
входов
на-
пряжения с номерами 1,
2,.mi
и
m2
входов
тока с номерами mi+1,
mi+2,
...mi+m2,
При
этом
m
= mi+m2.
Рассмотрим
схему преобразо-
ванной таким образом
цепи в обоб-
щенном виде (рис. 3.28).
Будем
обозначать входы напря-
жения индексом
а,
а входы тока — ин-
дексом b.
Определим
вектора напря-
жений
и токов на входах 2m-nonrocHHKa
N
в виде:
нентов.
Описание оставшейся линейной части
схемы может быть осуществлено просто
методами, о которых речь пойдет ниже.
Выделенные
элементы (двухполюсники) заменяются
независимыми источниками ЭДС или тока
по следующим правилам:
Управляемые
напряжением нелинейные сопротивления
заменяются независимыми источниками
ЭДС;
Управляемые
током нелинейные сопротивления
заменяются независимыми источниками
тока;
Емкости
(линейные и нелинейные) заменяются
независимыми источниками ЭДС;
Индуктивности
(линейные и нелинейные) — источниками
тока.
Входы
образовавшегося 2m-nonrocHHKa
(будем
обозначать его N)
(таких
входов 2m),
будем
называть входами напряжения или входами
тока по типу элемента, подключенного
ко входам (т.е. если некоторый элемент
заменяется источником ЭДС, то
соответствующие входы 2"-полюсникэ
называются входами напряжения, если
элемент заменяется источником тока —
то соответствующие входы называются
входами тока).
Предположим,
что у сформиро-
N
2m-norracHMK:
линейные
сопротивления, независимые источники,
линейные зависимые источники
Входы
напряжения
(а)
Рис.
3.28
m,
+1
Входы
тока
(в)
V
Ш!
+1
V
Ш1
+ 2
ib
=
mi
m1+m2
mi
+m2
По
принципу построения 2m-nonrocHHKa,
в
его составе остались независимые
источники ЭДС и тока, линейные резисторы
и зависимые источники тока и эдс
(линейные). Обозначим вектор независимых
источников внутри 2m-nonrocHHKa
в
виде и.
Т.к.
все элементы внутри 2m-nonrocHHKa
линейные,
то для него можно записать систему
гибридных матричных уравнений в виде: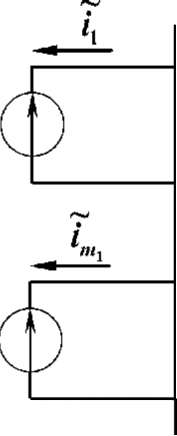
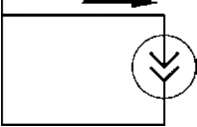
|
= H |
V a |
+ M U = H |
V a |
+ S |
v b |
|
|
|
|
|
т„ +1
т +т
т +т
2
m ! + 1
2
b
a
m
ii0
при
Va
=0,
b
=0.
Таким
образом компоненты вектора S
есть
токи закороченных входов напряжения
и напряжения на разомкнутых входах
тока при воздействии на схему лишь
внутренних источников энергии
2т-полюсника.
Рассмотрим
вопрос об определении параметров
матрицы Н. Для этого исключим все
независимые источники внутри N-полюсника,
при этом вектор S
обращается
в 0. Теперь компоненты матрицы Н
определяются из соотношения.
отклик
на входе j
"
i
J
возбуждение
на входе k
В
последнем соотношении устанавливаются
следующие условия:
Все
входы напряжения, кроме входа к замкнуты
накоротко, все входы тока, кроме входа
к разомкнуты.
Возбуждение
на входе к1
есть напряжение, если вход к1
— вход напряжения, возбуждение на
входе к есть ток, если к — есть вход
тока;
Отклик
на входе j
есть
ток, если вход j
—
вход напряжения, отклик на входе j
есть
напряжение, если вход j
—
вход тока.
Рассмотрим
вопрос о формализованном составлении
гибридных уравнений линейного
резистивного 2-n
полюсника
без управляющих входов.
ПРИМЕР.
Здесь
Ни M
—
некоторые гибридные матрицы, отражающие
связь токов входов напряжения и
напряжений входов тока с величинами
эдс входов напряжения, величинами токов
входов тока, а также влияние независимых
источников внутри 2т-полюсника N.
Очевидно, что судя по структуре уравнений,
матрицы Ни S
=
MU
можно
разбить на подматрицы в соответствии
с размерностью векторов va
и
ib.
Возвращаясь
к целям гибридного анализа, необходимо
отметить, что он имеет смысл не сам по
себе, а как удобный аппарат для решения
нелинейных уравнений, описывающих
схемы, а также дифференциальных уравнений
для расчета переходных процессов.
Рассмотрим,
каким способом можно хотя бы упрощенно
представить себе структуру гибридных
уравнений, точнее, гибридных матриц Ни
S.
Несложно
видеть, что из последнего уравнения
следует, что если закоротить все
источники ЭДС входов напряжения и
разомкнуть все источники тока входов
тока, то первое слагаемое в гибридном
матричном уравнении становится равным
нулю. При этом уравнение принимает
вид:
ab a
+ a
b
"ba "ЬЬ
ib
Sb
Н
V
- i |
Rb |
|
) |
J. 1 = 1 I Ra H R |
|
|
I T |
|
ii |
|
H a a |
H a b |
|
V a |
V 2 |
|
H b a |
H b b |
|
i b |
111
a
v
2
Рис. 3.29
=
Л
V
Rb
i i |
|
h11 |
h 1 2 |
|
Vi |
V 2 |
|
h 2 1 |
h 2 2 |
|
i 2 |
Ra
Рис. 3.30
Rc
i 2 =0
Ra!l(Rb + Rc )'
Rb
Rc
Рис. 3.3i
<i2
i
i
Ra ii (Rb + R c Г ~ Х Ж + Ш ~
Ra + Rb + Rc
Ra + Rb + Rc
h i i =
Ra-(Rb + Rc)
Ra + Rb + Rc R a -(Rb + Rc)
h = i i
■2 Vi=0
i2 -(RbllRc) R
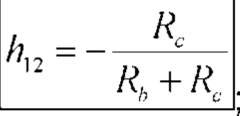
h
v
V
Rb
О
Г л
Ra
Rc
V2
h 21 = V2
1 i2 =0
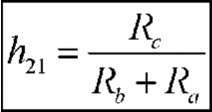
Рис. 3.32
Rb Г л - Ч ;
R
I T
Рис. 3.33
i2
V2
h 22 = V2
V1=0
Я Я Я + Я
2
h
2 2
3.6.2 Учет независимых источников напряжения и тока
Исключим из N -полюсника зависимые и независимые источники напряжения и тока. Таким образом, в гибридных уравнениях, описывающих схему, исключается вектор S. Для этого специального случая будем обозначать оставшуюся часть схемы 2и-полюсником N, опуская знак ~ в обозначениях токов и напряжений. Рассмотрим вопрос о существовании матрицы H для многополюсника, состоящего только из линейных резисторов.
Необходимым и достаточным условием существования гибридной матрицы для линейного резистивного многополюсника N является следующее:
i. Ветви, соответствующие входам напряжений, не содержат контуров;
ii2
2.
Ветви, соответствующие входам токов,
не содержат сечений.
Необходимое
условие
можно доказать методом от
противного
следующим образом. Предположим,
что
имеется 2 входа 2п-полюсника
N,
являющихся
входа-
ми напряжений, содержащих
контура. При этом эквива-
лентная
схема участка цепи, соответствующего
этим
входам будет иметь вид рис.
3.34.
Как
следует из принципиальной схемы
участка
цепи, величина тока через
контур, составленный из ис-
точников,
не определена. Если VjAV2,
то
ток в контуре стремится к
бесконечности;
если Vj
=
V2,
то
невозможно определить токораспре-
деление
в цепях Vj
и
V2.
Предположим,
что имеется 2 входа 2п-полюсника,
являющихся
входами тока, причем
входы образуют сечение, как показано
на рис.
3.35.
Если
источники тока равны друг другу по
величине, то невоз-
можно определить
величину установивщегося значения
напряжения
на них. Если значения
токов источников не равны друг другу,
то ре-
жим не определен. Таким образом,
необходимое условие доказано.
Рис.
3.35
Достаточное
условие
существования матрицы H.
Вспомним
свойства матрицы главных сечений
П.
По первому закону Кирхгофа
П1в=0,
где
Ie
—
вектор токов ветвей.
Выберем
дерево схемы таким образом, чтобы все
входы напряжений явились ребрами
дерева.
Так как по необходимому условию
существования матрицы
H
эти
входы не образуют
контуров, то это
возможно всегда. Обозначим ветви,
относящиеся к ребрам дерева и являю-
щиеся
входами напряжений индексом E.
Оставшиеся
ветви внутри 2п-полюсника, относящие-
ся
к ребрам дерева (т.е. линейные резисторы)
обозначим индексом R.
Обозначим
проводимости, от-
носящиеся к хордам
дерева и не яв-
ляющиеся
входами токов, индексом
G,
наконец,
проводимости ветвей,
относящиеся
ко входам токов и яв-
ляющиеся по
определению хордами
дерева, обозначим
индексом J.
С
учетом указанных обозначе-
ний
2п-полюсник может быть пред-
ставлен
эквивалентной схемой сле-
дующего
вида (рис. 3.36).
Так
как n-полюсник
N состоит
только из линейных резисторов,
то он
может характеризоваться
матрицей
сопротивлений.
При этом часть схемы, относящаяся к
ребрам дерева — матрицей резисторов
Zr,
а
часть схемы, относящаяся к хордам —
матрицей проводимостей
Ув.
Рассмотрим
более подробно соотношение
П1е=0.
Матрица
П,
по определению — пря-
моугольная
размером (vxl),
в
которой элемент яъ определяет
принадлежность s-ой
ветви
схемы k-ому
сечению. Если пронумеровать ветви
дерева таким образом, чтобы ребра дерева
|
|
|
D |
1 I |
С |
|
2n |
|
Рис. 3.34
|
1 |
1 |
|
I |
|
|
4 |
VE v )
2п-полюсник:
N линейных резисторов
VYJ J
О
Входы напряжения
E
R G рис. 3.36
Входы тока
J
113
получили номера от 1 до v, то, очевидно, элементы яъ, k=1, 2, ... v; s=1, 2, ... v будут составлять единичную диагональную матрицу, т.к. через одно ребро, по определению, проходит только одно сечение. Знак диагональных элементов — +1, т.к. направления сечений и ребер совпадают. Разбив матрицу Л" на подматрицы, таким образом, можно записать:
п и
EE 0 ER
'RE
RR
nEJ X R = 0
riRJ G
ребра хорды
В последнем уравнении левая подматрица представляет собой единичную диагональную матрицу размером (vxv), где v — число ребер, а правая подматрица — матрица, отображающая положение хорд относительно главных сечений. Токи входов напряжения, ребер, не относящихся к входам напряжения, хорд, не относящихся к входам тока, обозначены соответственно: IE, IR, I G, IJ.
Рассмотрим второй закон Кирхгофа в матричном виде:
г и в = 0
В матрице Г размера (cxl) каждый элемент rks определяет, как s-тая ветвь входит в k-ый контур. Т.к. по определению главные контура выбираются проходящими через хорды схемы, то в матрице Г можно выделить единичную подматрицу размера (схо), которая соответствует хордам. Т.к. все хорды нумеруются, начиная с (v+1) по порядку, то структура матричного уравнения по второму закону Кирхгофа имеет вид:
U E
г и Е
Г GE Пз R
Г J7 J- JR
V
ребра
GG 0GJ U
X
'JG JJ
а
хорды
U , U
Для дальнейшего доказательства теоремы рассмотрим соотношение П-Г1 и докажем, что П-Г = 0.
В скалярном виде последнее равенство означает, что для всех i и j должно выполняться равенство:
E
n E G
n R G
0
114
KeHmypj+1
Рис.
3.38
'i,s+1
"'
А
js
Очевидно
при этом, что
,
sr
J,s ,
s+1Г
J,s
+1
=
0
.
Рассмотрим
(j
+ 1) контур
(рис. 3.38), проходящий через
хорду
(s+2).
Элементами
матриц Пи Г, соответствующих се-
чению
i,
контуру
j
+ 1,
ветвям s
и
s+2
будут
значения:
1
i,
s+2
=
-1; Г
J,+1_s
=
+ 1 ; Г
J+1,s+2
=
1
При
этом, очевидно, справедливо равенство:
Щ
,s
rj
+
1 , s
+
Щ ,s+2
Г
J
+
1,s+2
=
0
с
[строка
i
матр.
П]•
[столбец
j
матр.
TJ
=
0
т
о
л
[строка
i
П]*
б
е
ц
=
о,
Г
1
где
i
=
1, 2,...,
v j
= 1,2,...&;
или,
что то же
[строка
i
матр.
Л]* [строка
j
матр.
ГТ = 0 .
Последнее
равенство можно записать в виде суммы
следующим образом:
самое,
is
Fs
=
о
i
=1,2,.-,
v
J
=1
■2,.
-v
s=1
В
сумме слагаемое, отличное от 0 имеет
место лишь в том случае, если некоторая
s-тая
ветвь входит одновременно в сечение i
и
контур J.
Предположим,
что имеется некоторое i-тое
сечение, совпадающее по направлению с
s-той
ветвью (ребром), и две хорды, s+1
и
s+2,
определяющие
два контура: j
и
j
+ 1. Предположим
далее, что контура имеют противоположное
к ребру s,
и,
следовательно, сечению i
направление.
Рассмотрим
j-тый
контур (рис. 3.37), для которого направ-
Сечение i
КонтУРл/у
+
1 ление контура (хорды) совпадает с
направлением сечения
(ребра).
Тогда для соответствующих элементов
матриц Пи Г справедливо:
=
1.
к,
1-
Г =
-
1 '
А1"
Рис.
3.37
Г
А
J,s+1
1.
Сечение
i
s+2
Таким
образом, для всех возможных соотношений
между ветвями, контурами и сечениями
соотношение П-Г1
=
0 доказано.
I
s
115
GG
0
GJ
x UR -
П LLg
-
riR
G
JG
JJ U
G
U
В
соответствии с рассмотренным выше
представлением матриц Пи Г в виде
единичных
подматриц
размером (vxv)
и
(gxg)
соответственно,
можно рассмотреть соотношение ПГ 1
в
виде:
ПГ1
= 1v
П
хорд X
Гребер
Г
t
ребер
1а
1v
П
хордХ
= Гр + Пх = 0
1а
Тогда
справедливо, что
Г1р
= - Пх Г =- П Х
Возвращаясь
ко второму закону Кирхгофа для метода
узловых потенциалов, можно запи-
сать:
г
и
ГGE
1
^GR
'
JE
2
JR
U
,
0
JG
JJ U
G
U
•n
EJ
n
RJ
U
E
1gg
0gj
х
ur
=
0
0
Для
схемы имеются также очевидные соотношения:
7
R
"r
L
YRVR.
G
YGVG
U
G
7
G
1
G
где
7r,
Yr
—
матрицы сопротивлений (проводимостей)
ребер;
Yg,
7g
—
матрицы проводимостей (сопротивлений)
хорд.
Для
составления матрицы H
необходимо
решить уравнения относительно
"e
и
Vj
при
заданных
значениях
Ve
и
"j.
(задача)
Запишем матричные уравнения по первому
и второму
законам Кирхгофа
г
U
„
= 0.
через
подматрицы. Получим:
1E
+
N E
G
1
G
+
П E
J
1
J
=
0
1R
+
n
R G
1
G
+
П
R
J
1
J
=
0
П
I
e
G V E -
H'RGVR
+
VG
=
0
•NJVE
-
П R
J V R +VJ =
0
Исключим
из второго уравнения вектора
"r
и
"g:
"r
=
YrUr,
"g
=
YgUg.
YRVR
+
NRGYGVG
+
ORJIs
=0
Третье
уравнение решим относительно VG:
(*)
VG
=
П E
G V E +
П R
G V R
Подставим
это выражение в уравнение (*), получим:
YRVR
+
HRGYG
[HEGVE +
H
R G V
R
)
+
NmIJ
=
0
а
"
Ш
и
= Л
116
или
YrVr
+
NrgYgNRgVr
=
-NrgYgHEdYE
-
HRJIJ
VR
=
[YR
+
ПRGYG
П RG
H -
ПRGGYG
ПEGVE
Пии
J
Исключим
из третьего уравнения системы
Vr
и
Vg.
-ПлуЕ
-
П R
G Z RI R +ZGIG =
0
Из
второго уравнения выразим
Ir:
1
R
=
-
П R
G
'
G
~
П R
J
1
J
.
»
Подставим
его значение в уравнение (***), получим:
-
URGVE
-
HRGZR
[-
HRGIG
-
П R
J I J ]
+ ZGIG
=
0
- URGVE
+
П R
G Z RURGIG +
П R
G Z RURJIJ +
ZGIG
=
0
'
G
\ P r GZ
R HRG
+
Z
G П
E
G
V
E л
r
gz
R л
r
j
i
j
Ig
^^GZRHRG
+
Zg
f1
[URGVE
Подставим
уравнение (****) в первое уравнение
системы:
IE
+
n
E G [
n
R
g
Z R n R
g
+
ZG
л
[URGVE
-URGZRПл
] + = 0
1E
=
-
PEG\HRGZRHRG
+ ZG]"
П
E
G
V
E
+ EG
\ P RGZ
R" R G
+
Z
G ]
" "RGZR"RJ
П
EJ
•
' ,
ИЛИ
IE
=
-
HEGZ
-1
URGVE
+
[ U
E G Z
-
1
ПRGZRПш
-
UEJ
]•
I
7
= 7 +
П
1
Z
П
^ л
1
1mr
g
^R
1
1
R
G
URG
=
[RX
G];
ПRG
=[G
XR]
Zr=ребра
2М-полюсника
Подставим
значение
Vr
из
формулы (**) в последнее уравнение
системы. Получим:
-
ПEJVE - nJ
YR +
URGYGnRG
J"1
[-
URGYGURGVE
~ Пю
1э
]+ VJ
=
0
Отсюда:
VJ
=
N J
V
e
-
П <
ш
[yr
+
URGYGNRGJ"1URGYGП<Е(УЕ
-
п<ш
[yr
+
П л
u
R
GлПш
J
Обозначив
Y
=
\yr
+
nRGYGnfRG
]
и приведя подобные члены:
=
\п' -П/Y-1
П
Y
П'
1-V
V-П
,11
1' (******)
J
V
EJ
RJ1 RG
G
EG
J
V
E 11RJ1
11RJ1J V J
Таким
образом, нами получена формула для
определения
Ie
и
Vj
через
значения эдс
входов напряжения и
токов входов тока:
117
n
j Y -
1
Л ш
Вспомним
исходное уравнение для гибридного
описания схемы:
'10
Рис.
3.39
В
схему входят 3 независимых источника
тока
и один независимый источник
напряжения. Выде-
лим все независимые
источники в виде входов тока
и
напряжения, соответственно. оставшийся
вось-
миполюсник является (2n,
n=4) чисто
резистивным,
следовательно для него
применимы все выводы
доказанной
теоремы.
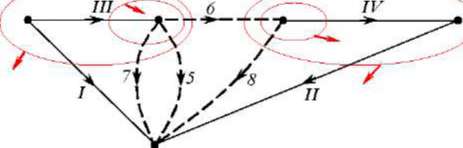
Лостроим
дерево схемы таким образом, что-
бы
ребра дерева проходили через входы
напряже-
ния, а хорды — через входы
тока рис. 3.41.
Лостроим
матрицу главных контуров схемы:
контур:
хорда 7, ветви 2, 1, 3, 4, 5, 6, 7
контур:
хорда 8, ветви 1, 2, 3, 4, 8.
контур:
хорда 9, ветви 4, 5, 9.
контур:
хорда 10, ветви 3, 4, 5, 6, 10
Лри
этом матрица главных контуров имеет
вид:
10
4-
Рис.
3.41
I
V
-
Л
7
Л 1
EG'
11
EG
Л
EG
7
Л
U7
R nRJ
-
Л
Mf
V Л
Y
Лf
1
1
R
J 1 RG
G EG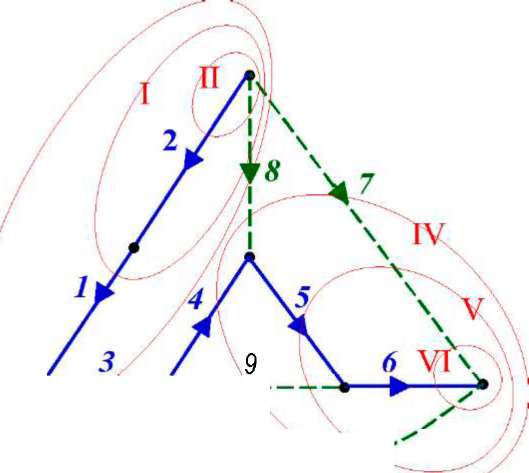
|
V E |
X |
|
|
1 J |
|
|
Н |
|
|
I E |
|
aa Н a h |
|
V E |
|
= |
|
X |
|
V J |
|
Н h a H h h |
|
I J |
Таким образом, последнее полученное выражение дает не только факт возможности расчета элементов Haa, Hab, Hba, Ньь гибридной матрицы, но и их числовые значения, выраженные через параметры 2и-полюсника. Рассмотрим ЛРИМЕР.
Лостроить гибридную матрицу для схемы, изображенной на рисунке:
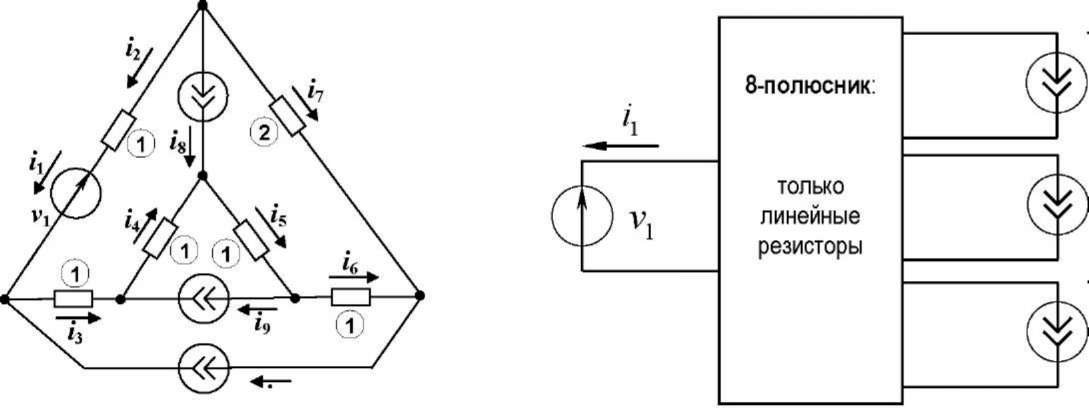
40
Рис. 3.40
E
8
9
118
Пее
= 1
0
0
0
nER
=
[0 0 0 0 0]. nEG
=
1
1 0 0 0
0
0 1 0 0
0
0 0 1 0
0
0 0 0 1
0
0 0 0 0
1
Построим
матрицы
Zr,
Zg
,
YR,
yg:
1
0 0 0 0
0
10 0 0 0 0 10 0 0 0 0 1 0 0
0 0 0 1
1
0 0 0 0
0
10 0 0
0
0 1 0 0
0 0 0 1 0
0 0 0 0 1
E |
|
|
R |
|
|
G |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
-1 |
- 1 |
- 1 |
- 1 |
- 1 |
- 1 |
1 |
0 |
0 |
0 |
1 |
-1 |
- 1 |
- 1 |
- 1 |
0 |
0 |
0 |
1 |
0 |
0 |
2 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
3 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
4 |
Построим аналогично матрицу главных сечений:
R
G
n =
1 |
0 |
0 |
0 |
0 |
0 1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 1 |
1 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
0 |
0 1 |
1 |
0 |
- 1 |
3 |
0 |
0 |
0 |
1 |
0 |
0 1 |
1 |
-1 |
- 1 |
4 |
0 |
0 |
0 |
0 |
1 |
0 1 |
0 |
-1 |
- 1 |
5 |
0 |
0 |
0 |
0 |
0 |
1 1 |
0 |
0 |
- 1 |
6 |
Выделим подматрицы матрицы П:
R Е
0 0
RG
RJ
ZR
z G = 2
Yg = zg1 = |0,5|
= 11 0 0J
1 0 0 1 0-1
1-1 -1
0-1 -1 0 0-1
Найдем элементы Z и Y:
1 0
п
Y
Z
R " R
119
1
0 0 0 0
0 10 0 0
0
0 10
0
0 0 1
7
-
7g
+
HRGZRHRG
-
2 + [1
=
2 + 5 = 7
1111]
7
-1
0
= 2 + [1
0
1111]-
0
0 0 0 1 1
±
-
Y
± -R П
n
rgY-
gI
RG
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 + |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0,5 • 11 1 1 1 1l
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 + |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0,5 0,5 0,5 0,5 0,5 =
1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1
Y
0,5 0,5 0,5 0,5 0,5
0,5 0,5 0,5 0,5 0,5
0,5 0,5 0,5 0,5 0,5
0,5 0,5 0,5 0,5 0,5
0,5 0,5 0,5 0,5 0,5
6 7
1 7
1 7
1 7
1 7
После выполнения действий:
1 7
6 7
1 7
1 7
1 7
1 7
1 7
6 7
1 7
1 7
П 7~1nf
E G " 11 EG
1,5 0,5 0,5 0,5 0,5
0,5 1,5 0,5 0,5 0,5
0,5 0,5 1,5 0,5 0,5
0,5 0,5 0,5 1,5 0,5
0,5 0,5 0,5 0,5 1,5
1 7
1 7
1 7
6 7
1 7
+
120
Выше
была доказана теорема о существовании
гибридной матрицы для линейного
рези-
стивного 2п-полюсника, не
содержащего внутри себя независимых
источников тока и ЭДС. Ее
выводы
легко можно распространить на случай,
когда 2п-полюсник содержит внутри себя
не-
зависимые источники энергии.
Рассмотрим
2т-полюсник N,
составленный
из следующих основных элементов:
линей-
ных положительных сопротивлений,
kj
независимых
источников ЭДС, k2
независимых
источни-
ков тока. Будем обозначать
напряжения и токи на входах независимых
источников эдс vp
и
ip,
токи
и напряжения на входах независимых
источников тока iq
и
vq
(рис.
3.42).
Для
проведения доказательства выделим из
2т-полюсника вначале все независимые
ис-
точники энергии в качестве
отдельных входов. (При этом, естественно,
будем предполагать,
что кроме
выделенных источников, 2т-полюсник
имеет «обычные» входы напряжения и
тока,
обозначенные параметрами
~a,
ia,
~b,
ib).
При
этом вновь образуется чисто резистивный
2и-полюсник,
эквивалентный исходной схе-
ме, но
имеющий на 2(k1+k2)
входов
больше
(рис.3.42).
Для
вновь образованного
2n-
полюсника
можно записать, что:
v
Рис.
3.42 Vr
v
H
a b
П
E
G z
П
R
G z
R HRJ
E
J
Получим:
H
ь.
--П1
- П 1 Y
~1П
Y
П
1
ba
E
J
H
b b
R
J '
RG
J-G1
1
EG
-
U
1
R
J Y
-1
"
R
J
4
7
2
7 4 7
12
7 1 7 2 7
1
7 10 7 6 7
2
7 6 7 12 7
vp
iP
k1
2n-
полюсник:
q
vq
k2
только
линейные резисторы
VE
=
1
1
H
ab
a
a
1
4
2
4
v
7
7
7
7
v
8
8
v
9
9
v
H
ba
H
bb
v
v
a
L
a
a
b
h
q
i
j
q
Если
соблюдается необходимое и достаточное
условие существования гибридной
матри-
цы для 2п-полюсника, то, очевидно,
для него можно записать:
121
H
ab
H
a q
Hpa
нрр
Hpb
H
2 3
0 0
1 0
0
0 1
1
-
1
-
1
2
2
'a |
|
1 p |
|
V q |
|
a a
H
H
p q
H b a H b p Hbb H b q
q p
q b
|
V a |
|
V~p |
|
~b |
|
'q |
Последнее уравнение записано для 2и-полюсника, содержащегося внутри 2т-полюсника. Нас, в принципе, не интересуют значения токов через выделенные независимые источники эдс и напряжения на выделенных независимых источниках тока. Поэтому из соответствующей системы уравнений можно исключить уравнения относительно ip и vq. При этом получим:
H b a H b p
H a b H b b
H aq H b q
Или, записывая уравнения в несколько ином виду, получим:
ia |
|
Haa |
H ab |
|
|
+ |
H a p |
H a q |
|
Vp |
v b |
|
H ba |
Hbb |
|
|
|
H b p |
H b q |
|
'q |
Таким образом, выявилось в явном виде значение матрицы источников S , а также матрицы H в виде:
ПРИМЕР 1.
Е
0
П =
П ЕЕ = 11
П RE
Z F
2 0 0 2
S = |
H a ap |
H a aqq |
H = |
H a a |
H a b |
|
H b p |
H b q |
|
H b a |
H b b |
■1 |
|
h11 |
h12 |
|
V1 |
V 2 |
|
h21 |
h22 |
|
'2 |
R
G
1E 2R 3R
П л = 0 0 1 0
П RR
YR
0 1
0,5 0 0 0,5
nEG 1
П RG
ZG = 4
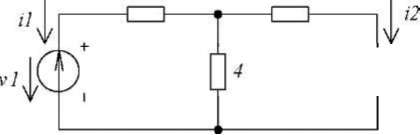
Рис. 3.43
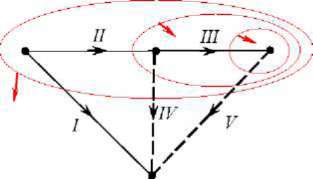
Рис. 3.44
П eJ
П RJ
11
1 1
Yg = 0,25
q a
a
v
a a
a p
b
V
b
q
4
5
0
1
0
122
-
2
0
=
-(4/3 + 2 ) = - з ! = -10/3
Нахождение
методом возбуждений-откликов
-
1/6 - 2/3
2/3
-10/3
ПРИМЕР
2.
2
" 2
-CZb Е
ba
= nJ - n1
R J Y 1
U r g 7
g n f
e G =
1
Z
=
Zg
+
n'RGZRnRG
=
4 + -1 0
2
0 0 2
=
4 + - 1 0'
|
0,5 |
0 |
|
-1 |
|
0,5 |
0 |
|
-1 |
Y = Y± R+ П R GYG П RG = |
0,5 |
+ |
0 |
1 0 = |
0,5 |
+ |
0 • |
||
|
0 |
|
0 |
|
0,5 0 |
|
0,25 0 |
|
0,75 0 |
0 0,5 |
+ |
0 0 |
|
0 0,5 |
Y = 0,375
4 + 2 = 6
- 0,25 0 =
H
H
П Z — i n t
j'i'e g л eg
1 '6M 6
ПЕ£ Z n<jRRnRJ- ПJ = 1 • - 6
2 0-1 - 2 -1 0 • -1 = - .1-1 0 • -1 0 2-1 6 - 2
= 1•2-1 = -2 6 3
-1 |
|
4/3 |
0 |
|
-1 |
-1 |
|
0 |
2 |
|
0 |
0,25-1 = 1
= 1 - 0,25
• 4 = 22
3 3
bb J
R
G
-1 |
|
4/3 |
-1 |
|
0 |
4/3 0 |
|
-1 |
4/3 |
|
|
|
- - 1 - 1 • |
0 2 |
|
-1 |
- 2 |
Рис. 3.45
П
0,25
i |
2 |
3 4 |
5 6 7 |
8 |
|
1 |
0 |
0 0 |
1 1! 1 |
0 |
1E |
0 |
1 |
0 0 |
0-1 0 |
1 |
2E |
0 |
0 |
1 0 |
T - ■1.1 1 |
0 |
3R |
0 |
0 |
0 1 |
0 -1 0 |
1 |
4R |
Рис. 3.46
I
0
H
1
RJ
'2
123
-
1
-
1 -1 =
0-1
4
0 0 2
7
= 7 + П' 7 П
Y
=
Yr
T+ HP rG±YGHP Rg
3.6.3
Учетуправляемых источников при
формировании гибридной матрицы
При
наличии в схеме управляемых источников
проблема формирования гибридной
мат-
рицы существенно усложняется.
Одной из важных задач является определение
типа элемента
замещения: каким из
входов, входом напряжения или входом
тока является замещаемый эле-
мент.
Предположим,
в схеме имеется нелинейные резисторы,
которые могут быть представле-
ны
либо входами напряжения, либо входами
тока, а также зависимые источники ЭДС
и тока
(рис. 3.47).
Предположим,
что оба входа явля- „ .
ются
входами напряжения, тогда гибрид-
ные
уравнения 4-хполюсника имеют вид:
6
Ом -CZb
'4
Внутри
2п-полюсника отсутствуют
независимые
источники ЭДС, поэтому
вектор
источников S
равен
0.
Определим
коэффициенты матрицы
H
путем
исследования откликов входов схемы.
Найдем
коэффициент hn,
рассмотрев
условие: v1
-
задано; v2=0,
т.е.
элемент закорочен:
П
1
0 =
0 1
0
0
7
R
"
0 0
4
0 0 2
YR
0
0 " 0 0
1
0 = 0 1
0,25
0 0
0,5
П
я а
П
R
G
П
П
RJ
YG
1
0 " 0 1
-1
0 = 0 1
0,25
0 0 0,5
'2
V
7
Vc
ab
Vn
H
ь
Hbb
3
Ом
|
|
h n |
h 1 2 |
|
V1 |
~2 |
|
h 2 1 |
h 2 2 |
|
V 2 |
'' v l
V
v5 = 2*'3
v6 = k*'4
-у-
v2 . '2
-у-
-y-
Рис. 3.47
13-N, 1 4—12
9a = -(2 • i3 + k • i4 ) = 2 • ii - k • i4
3 Ом
О
' - Ф a -
'4 " 6 "
2
V
k' ' <
|
< — |
|
'4 Zv5 = 2*'3 |
6 Ом
v6 = k*'4 Рис. 3.48
■4
1
п
П RE
П RR
V
a a
7
8
|3
'3
/'1
V
6
2
4
6
2
124
6
- k
; з
= _ ■ i
6
• i4
+
2 • ii
-
k
•
i4
=
0 2
• i
'4
=
л
" k
-
6
2k
•
ii
2k •
ii
-12
• ii
-
2k
•
ii
-12
• ii
k
- 6 k - 6 k - 6
Из
величин коэффициентов матрицы следует,
что при k
= 2
матрица
не существует, т.к.
элементы hj
обращаются
в бесконечность. Рассмотрим случай,
когда в той же схеме один из
нелинейных
резисторов представляется
входом
напряжения, а второй — входом
тока.
Структура
матричных уравнений при
этом:
этом
i2=0,
т.е.
второй вход
2т-полюсника
разомкнут:
4Z3—
v1 i3
и
ra
-СоК
i
4
+3
1
2
Фа
= - 2
* i3
+
k
Ф
а
U
-
?
Фа
= 2
• '1
-i
2
• i
л
-1
2
- 3k
+i 8
6 - 3k
Vi
=
Ф а + '3
k-
¥
-3
•
'1
= '1
k
- 6
k
-
6 i
1
/i
k -
6 vi
6
- 3k
По
аналогии определяются другие коэффициенты:
6 - |
k |
k |
3k |
6 |
3k - 6 |
2 |
|
1 |
3k - |
6 |
3k -6 |
v v
3 Ом 4ZZ1—
6 Ом
-а
vi
i3
/1
v5 = 2* i 3
i 4
V
v2
v6 = k*i 4
Рис. 3.49
t-
■1 |
|
h 1 1 |
h 1 2 |
|
v 1 |
v 2 |
|
h 2 1 |
h 2 2 |
|
■2 |
Определим коэффициент hii, При
h.1 = ±
О
V
v5 = 2* i 3
v6 = k*i4
'2 - '4 - 0 л
У6 = 0
Фа
■3 . ч
= Фа
Рис. 3.50
v1 = - 2 • ■З + 3 • ■З = ■З ■1 = - ■ 3 . v 1 = - ■ 1 . h11 = -1
По аналогии схема для определения hi2:
3
3
2
= 0
125
/т
—-Фа
-
3 3
Аналогично
определяются остальные коэффициенты.
При этом матрица имеет вид:
1
k
Таким
образом, правильный выбор входов
напряжения и тока в значительной
степени
определяет успех построения
гибридной матрицы. При неправильном
назначении входов мат-
рица вырождается.
Рассмотрим
способ формирования гибридной матрицы,
который называется методом
выделения
управляемых источников.
Рассмотрим
схему некоторой цепи вида рис. 3.52.
Указанная
цепь представляет собой 2m-
полюсник,
в котором
m=1.
Гибридное уравнение, опи-
сывающее
схему, должно иметь вид:
n
= hjj-v1.
Заменим
вначале управляемый источник тока
независимым
источником и выделим его во вход тока.
Эквивалентная схема цепи примет вид
рис.
3.53.
А
гибридное уравнение, описывающее схему
в
этом
случае, имеет вид: -C3-
'' Rb
3
Ом
Рис.
3.51
l>2
v2
3
• ' 2 * /3 k' ?2
h
= л
12
■2
v1=0
■4
= ■ 2
0
V2
=
Фа
+'4 •
6
Фа
= -2
■
^
J. k
.
■ о
2
* /3 k' '2
-k
•
L
4
'3
k'„
hn
= л = k
H
=
2
3k - 6
-CZb
Rb
V1&
\Ra
>Р1а
Рис.
3.52
'2
R„
1
-1
v
•Ru
2
v'&
Ra
Рис.
3.53
Коэффициенты
матрицы легко определить по откликам
входов. Однако ток
'2 не
является независимым, а определяется
током резистора Ra.
С другой стороны, ток резистора Ra
не входит в координатный базис
гибридного уравнения, поэтому обычным
способом определен быть не может. Для
устранения этой трудности введем еще
один дополнительный фиктивный вход в
рассматриваемой схеме, представляющий
собой вход напряжения с напряжением,
равным 0, в результате чего получим
эквивалентную схему рис. 3.54:
3
2
v
126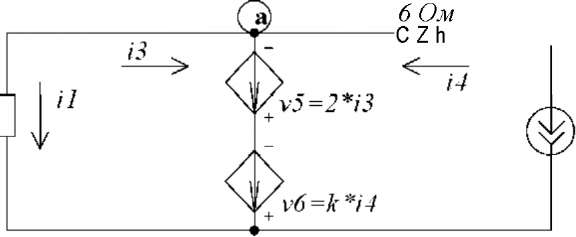
; Рис.
3.54
Для
того, чтобы полученная схема была
эквивалентна исходной, необходимо
записать дополнительно 2 условия:
V3
= 0 ; i2
= pi3
у
Для
получения гибридной матрицы в искомом
виде, необходимо исключить 4 нежелательных
переменных i2,
v3,
V2,
i3.
Для
этого запишем гибридные уравнения
вначале в обычном виде:
i
= v - i н v
-
Ra Ra
Она,
в свою очередь описывается гибридным
уравнением вида:
1
R
1
1
-1
1
R
Rb
vh
■1
Рассмотрим
условия:
Тогда,
очевидно,
v
2
- v
- -
R
b •
'2
1 1
h
- 'м v3
R - -
R
3
V3
- 0 ; i2 - pi;
-
- R
-
- v
,
-
p
.
R
-
-v,
•
R
(p
+1)
откуда
P
+ 1
hn
- Л - '
v
R„
что,
собственно, и требовалось определить.
Таким
образом, суть метода выделения
управляемого источника состоит в
выделении правильного набора элементов
из 2т-полюсника, в результате чего
удается воспользоваться уравнениями
для гибридного резистивного 2п-полюсника.
Гибридный
анализ распространен нами на следующие
виды элементов электронных схем:
линейные сопротивления, все типы
управляемых источников, независимые
источники ЭДС и тока, а также нелинейные
элементы, каждый из которых представляется
либо управляемым напряжением
источником тока, либо управляемым током
источником ЭДС. Кроме того, идея метода
управляемых источников позволяет
также, при желании, обеспечит расчет
напряжений и токов в любой точке
схемы, т.к. для введения указанных
параметров в координатный базис схемы
достаточно включить в ветвь, в которой
необходимо рассчитать ток, фиктивный
источник ЭДС с напряжением, равным
нулю, а между точками, в которых необходимо
рассчи
2
2
1
'3
127
тать
напряжение — фиктивный источник тока,
с током, равным 0. При этом фиктивные
элементы выносятся из схемы в виде
входов напряжения и тока, соответственно,
что позволяет рассчитать их основные
параметры.
Не
следует забывать, что вся теория
гибридных матриц выведена в принятом
ранее допущении, что независимые и
управляемые источники тока не образуют
сечений.
Расссмотрим
формализованные методы составления
гибридной матрицы для схем с зависимыми
источниками.
Допустим
имеется n таких источников.
Каждый источник может быть управляемым
током замкнутого накоротко элемента,
или узловым напряжением на разомкнутом
элементе. Это не снимает общности, т.к.
замкнутый элемент может быть всегда
добавлен последовательно с любым
элементом схемы, а разомкнутый элемент
— параллельно. Однако ограничения на
вид схем тем не менее имеют место:
Зависимые
источники напряжения, входы напряжений
и независимые источники напряжений
не образуют контуров.
Зависимые
источники токов, входы тока, независимые
источники тока не создают сечений.
Такую
схему в целом можно представить в виде:
Выделяем
независимые и управляемые источники
напряжения во входы напряжения.
Выделяем
короткозамкнутые элементы (токи
которых являются управляющими
переменными), во входы напряжения
(с напряжением равным 0).
Независимые
и зависимые источники тока выделяем
во входы тока.
Разомкнутые
элементы, напряжения на которых
являются управляющими переменными
для зависимых источников, превращаем
во входы тока (с током, равным нулю).
Обозначая:
Va
— входы напряжения
ve
— независимые источники напряжения
vvv
— управляемые напряжением источники
напряжений
vcv
— управляемые током источники
напряжений
vsv
— короткозамкнутые независимые
элементы
b
— входы тока
j
— независимые источники тока
сс
— управляемые током источники тока
vc
— управляемые напряжением источники
тока
ос
— разомкнутые элементы
Векторы
напряжений входов напряжения, токов
входов напряжения, токов входов тока,
напряжения входов тока:
128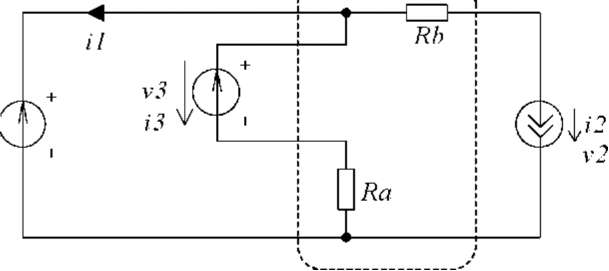
V.
V„
V.
v„
V
V
E
VV
Тогда
гибридная матрица имеет вид:
|
|
hn |
h 1 2 |
h 1 3 |
h 1 4 |
h 1 5 |
h 1 6 |
h 1 7 |
h 1 8 |
h 1 9 |
h "110 |
'e |
|
h 2 1 |
h 2 2 |
h 2 3 |
h 2 4 |
h 2 5 |
h 2 6 |
h 2 7 |
h 2 8 |
h 2 9 |
h 2 1 0 |
' v v |
|
h 3 1 |
h 3 2 |
h 3 4 |
h 3 4 |
h 3 5 |
h 3 6 |
h 3 7 |
h 38 |
h 39 |
h "310 |
' c v |
|
h 4 1 |
h 4 2 |
h 4 3 |
h 4 4 |
h 4 5 |
h 4 6 |
h 4 7 |
h 4 8 |
h 4 9 |
h "410 |
hv_ |
|
h 5 1 |
h 5 2 |
h 5 3 |
h 5 4 |
h55 |
h 5 6 |
h 5 7 |
h 5 8 |
h 5 9 |
h "510 |
~b |
|
h6 1 |
h 6 2 |
h 6 3 |
h 6 4 |
h 6 5 |
h66 |
h 6 7 |
h 6 8 |
h 6 9 |
h "610 |
|
|
h 7 1 |
h 7 2 |
h 7 3 |
h 7 4 |
h 75 |
h 7 6 |
h 7 7 |
h 7 8 |
h 7 9 |
h 7 1 0 |
vcc |
|
h 8 1 |
h 8 2 |
h 83 |
h 8 4 |
h 8 5 |
h 8 6 |
h 8 7 |
h 88 |
h 89 |
h 8 1 0 |
vvc |
|
h 9 1 |
h 9 2 |
h 9 3 |
h 9 4 |
h 9 5 |
h 9 6 |
h 9 7 |
h 9 8 |
h 9 9 |
h 9 1 0 |
v oc |
|
h 01 |
h "10 2 |
h "10 3 |
h "10 4 |
h "10 5 |
h "10 6 |
h "10 7 |
h 10 8 |
h "10 9 |
h "10 10 |
и необходимо вывести уравнения |
связи 'a, Va |
Vb |
v, i |
|
|
||||||
егр |
упп |
ируем матр |
ицу: |
|
|
|
|
|
|
|
|
|
|
h 11 |
h 1 6 |
1 h 1 3 1 |
h 1 9 |
h 1 4 |
1 h 1 8 1 |
h 1 5 |
"h1 10 |
j h12 |
h 1 7 |
|
|
h61 |
h66 |
h 63 |
h 6 9 |
h 6 4 |
1 1 h 6 8 1 |
h 6 5 |
h 6 1 0 |
■ h 6 2 1 |
h 6 7 |
'vv |
|
h 3 1 |
h 3 6 |
h 33 |
h 39 |
h 3 4 |
h -f1 38 1 |
h 3 5 |
h "310 |
h 32 |
h 3 7 |
vvc |
|
h 9 1 |
h 9 6 |
h 93 |
h 99 |
h 9 4 |
h 11 98 1 |
h 9 5 |
h "910 |
h 92 |
h 9 7 |
'cv |
|
h 4 1 |
h 4 6 |
h 4 3 |
h 4 9 |
h 4 4 |
1 h 4 8 1 |
h 4 5 |
h "410 |
h 4 2 |
h 4 7 |
v c c |
|
h 8 1 |
h 8 6 |
h 8 3 |
h 89 |
h 8 4 |
h 11 88 1 I |
h 8 5 |
h 810 |
h 8 2 |
h 8 7 |
'sv |
|
h 5 1 |
h 5 6 |
1 h 5 3 |
h 5 9 |
h 5 4 |
1 h 5 8 1 |
h 5 5 |
h 5 1 0 |
1 h 5 2 |
h 5 7 |
|
|
01 |
h "10 6 |
h 1 "10 3 |
h "10 9 |
h 1 0 4 |
h 11 1018 1 |
h "10 5 |
h "10 10 |
h 1 "10 2 |
h "10 7 |
'e |
|
h 2 1 |
h 2 6 |
h 23 |
h 2 9 |
h 2 4 |
1 h 2 8 1 |
h 2 5 |
h 2 1 0 |
h 22 |
h 2 7 |
|
|
h 7 1 |
h 7 6 |
h 7 3 |
h 7 9 |
h 7 4 |
1 h 7 8 1 |
h 75 |
h "710 |
h 7 2 |
h 7 7 |
~a ve vvv vcv
'vc
|
~a |
|
A |
|
vvv |
|
'vc |
|
vcv |
|
1 c c |
|
vsv |
|
ve 'j |
b
a
b
a
e
I
л
v
129
W1
=
H11
X
1
+
H12
X2+
H14
x
4
X2
=
K [H31X1
+
H
5
2X2
+
H34X4
]
.
>
I1
-
K
H 3
2
]X2
=
K
H 3
1X 1 +
K
H 3
4
X
4
•
>
x2
=
I1 "
K
H 3
2 ]
1
[KH31X1 +
K
H 3
4
X
4 ]
W1
=
H
4
X
1
+ H
1
2
[1 -
KH32
Г
KH31X1
+ H12
[1
-
KH32
Г1
KH34
X4+H14X4
11
H
1
2 ' 1 3 " 1 4
21
" 2 2 " 2 3 ' 2 4
H
31
H
32
H
34
H
3
4
H
41
H
4
2 H
4
3 H
4
4
X
3
=
Vsv
=
0
W3
=
напряженияуправляемых
источников, которые связаны с
напряжениями
и токами функциями управления K.
X
2 =
v V V |
0 |
k V V |
|
1 V |
0 |
Kc |
SV |
v c V |
" k c V |
0 |
V oc o c |
1 c |
k c c |
0 |
|
= KW.\
H 3 1 X 1 + H 32 X 2 + H 34 X 4
X2 "KH31X1 + KH 32X 2 + KH34X4
V
w,
H11 + H12 I1 " K H 3 2 I"1 K H 3 1
Я 1 2 f - K H 3 2 ] 1KH34 + H 1 4
i a |
= H • |
Va |
+ M • |
e |
~Ъ |
|
|
|
i j |
h = Я 1 1 + " K H 3 2 ] 1 K H 3 1 .
M = H14 + H12 [1 - KH32 Г KH 3 4 •
>
3.6.4 Метод Ньютона-Рафсона для гибридных уравнений
Предположим имеется нелинейная резистивная схема N, содержащая линейные и нелинейные (управляемые током и напряжением) сопротивления, независимые источники тока и ЭДС, все 4 типа управляемых источников. Предположим, что немонотонно изменяющиеся сопротивления сечений не образуют.
Вынесем все управляемые напряжением нелинейные сопротивления во входы напряжения, все управляемые током сопротивления — во входы тока. Их будет, соответственно,
X
W
X
2
2
W
X
3
3
W
X
4
4
V
oc
V
vc
V
cc
+
V
Ъ
130
шл
и m2.
В результате получим
2m-nonrocHHK
N, состоящий из линейных резисторов,
линей-
ных зависимых источников, а
также независимых источников энергии,
имеющий 2ш входов:
2m
= 2(mj+m2)
(рис. 3.55). Для ука-
занного
N-полюсника выше получе-
ны
соотношения, позволяющие соста-
вить
гибридную матрицу и описать ее
уравнениями
вида:
~a |
|
H a a |
H a b |
|
Va |
+ |
S a |
Vb |
|
H b a |
Hbb |
|
V b |
|
Sb |
Здесь вектор S — вектор неза- висимых источников энергии внутри 2т-полюсника. Несложно понять, что
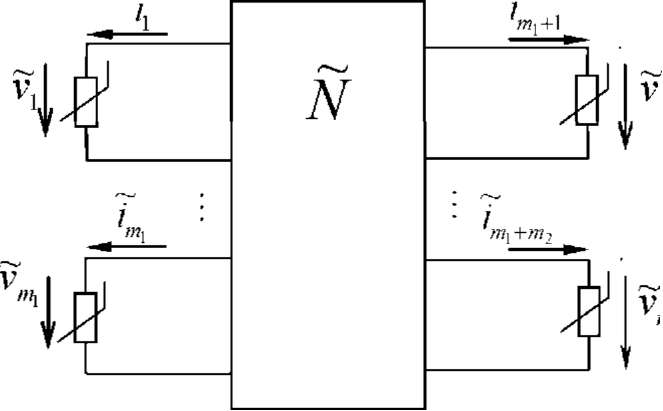
Рис. 3.55
все элементы правой части указанного уравнения, а именно Я и S не зависят от вида нели- нейностей, представленных во входах напряжения и тока. Поэтому при расчете схемы они всегда будут вычисляться только один раз.
Рассмотрим описание нелинейных элементов схемы (т.е. входов схемы). Управляемы напряжением нелинейные резисторы могут быть описаны нелинейными проводимостями, зависящими от напряжения:
S M
S 2 ( V 2 '
(Va )
2
mj S mj VV mj )
Управляемые током нелинейные резисторы на входах тока могут быть описаны нелинейными сопротивлениями, зависящими от напряжений:
V mj+j |
|
Rm; + i (Vm i + 1' |
Vmj + 2 |
= |
R m j + 2 (Vm j + 2 ) |
V ■ 2 mj+m2 |
|
Rmj+m2 (Vmj+m2 ) |
Несложно видеть, что напавления токов и напряжений на сопротивлениях и проводимо- стях совпадают с положительными направлениями токов и напряжений на входах 2т- полюсника. Поэтому можно подставить в левой части гибридных уравнений соотношения, описывающие нелинейные элементы и раскрыть уравнения в виде:
G (Va ) - HaaVa ~ H J ь ~ ~ =0
Rb (Ib) - HbaVa - Hbbib - Sb = о
В указанной системе нелинейных уравнений собственно нелинейными являются только члены Ga (Va) и Rb (Ib).
Обратим внимание, что последние уравнения записаны в виде, соответствующем решению методом Ньютона-Рафсона, а именно:
131
\F(Va
,
lb
)
= 0 I
F2(Va,
lb) =
0 Тогда
Якобиан указанных уравнений находится
в виде:
J=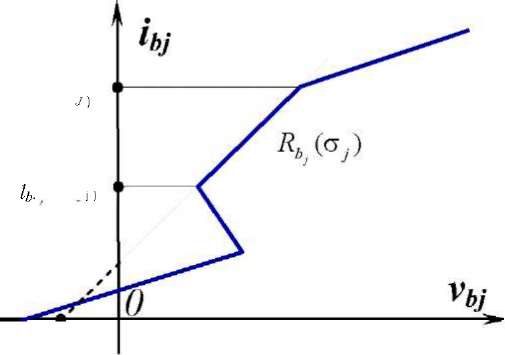
Щ |
Щ |
dVa |
dlb |
dF2 |
dF2 |
dVa |
dlb |
G h |
- H a b |
dVa " |
|
|
d R b H |
- H b a |
AT H b b |
Итерационная формула метода Ньютона-Рафсона имеет вид:
X7+1 = X7 -[j(XJJ]"1 F(XJ)
X = Т.к. b TO
y J
VJ
b J
Л G J H |
|
|
- H a b |
D V A a a |
|
|
dRb h |
- H b a |
AT H b b |
G a (V aJ ) - Haa (V )
l J ) - S J
R b (lb ) - Hba (VJ ) - Hbb (U )
Практическая реализация метода Ньютона-Рафсона для гибридных уравнений трудностей не представляет, т.к. начальное приближение может быть определено либо из оценочного расчета, либо, в худшем случае, задано нулевое начальное приближение. Однако серьезным недостатком метода является то обстоятельство, что матрицу Якоби необходимо рассчитывать и обращать на каждом шаге решения нелинейных уравнений.
Существует, однако подход, который позволяет избавиться от этого недостатка. Он состоит в том, что нелинейные характеристики сопротивлений заменяются их кусочно-линейными аппроксимациями. Рассмотрим характеристики входов напряжения и тока в некоторой нелинейной схеме рис 3.56.
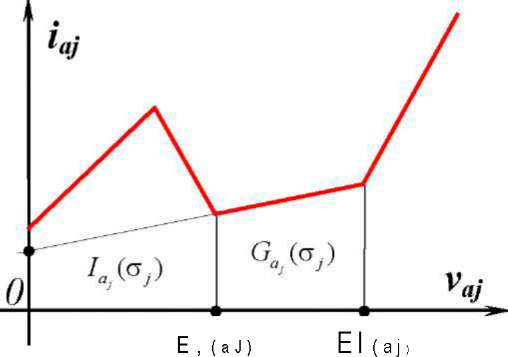
Eb{Oj)
Рис. 3.56
Как видно на рисунке, характеристика нелинейного сопротивления, управляемого напря- жением, на участке напряжений E~ (a.) < Vaj < E+a (a.) описывается уравнением:
'aj = G a j J ) V a j + ' a j ( ° J )
+ 1
b
132
Аналогично,
характеристика нелинейного сопротивления,
управляемого током (входа тока)
научастке /" (ст
j)
<ibj
< 1+ъ
(a
j)
описывается уравнением:
v
bj =
R
b j J )1
bj
+
E
b j J
)
_
Выберем
одну из комбинаций отрезков ст и
обозначим их таким образом, чтобы CTI
соответствовало первому входу,
Ст2 — второму; ami+i — (mi+1)
входу тока и т.д. Очевидно, что для
определения принадлежности текущей
точки тому или иному интервалу расчета,
необходимо сравнить значения
управляющих напряжений на входах
напряжений с границами E~ (ст
j),
E+a
(ст
j)
итоков входов токов — страницами
I" (ст
j),
(ст
j).
Как
видно из приведенного рисунка (рис.
3.56), на каждом участке справедливо
описание ВАХ нелинейного сопротивления,
управляемого напряжением, в виде:
1 a 1 |
|
G a 1 ( Л 1 1 |
0 |
0 |
|
va 1 |
|
|
1 a 2 |
= |
0 |
G a 2 ( °2) • |
0 |
X |
v a 2 |
+ |
1 a 2 ( ° 2 ) |
i .mi |
|
0 |
0 |
G a m l ( P ml1 |
|
v am1 |
|
'am 1 ( P m 1 1 |
Аналогично, ВАХ нелинейного сопротивления, управляемого током —
v bm1+1 |
|
Rbm1 + 1(Am1+1) |
0 |
0 |
|
ib m1 +1 |
|
Em i + 1(® m1 + 1) |
vbm 1 + 2 |
= |
0 |
Rbm1 + 2 (л m 1 + 2 1 |
0 |
X |
lbm1+2 |
+ |
E m 1 + 2 л P m 1 + 21 |
v bm1+m2 |
|
0 |
0 |
Rb mi+m2 ^m 1 +m2 ) |
|
'bm1+m2 |
|
Em1+m2 m1+m2 ) |
Причем напряжения и токи должны соответствовать матричным неравенствам:
E~a1 (-1 ) |
|
va 1 |
|
E a + 1 K ) |
E a2(-2> |
< |
v a 2 |
< |
E a + 2 ( - 2 ) |
E am1 m1 ) |
|
v am1 |
|
E am1 (a m1 ) |
1 bm1 + 1 ( P |
m1+1) |
|
^m |
1+1 |
|
1 bm1 + 1 (P |
m1+1) |
1b m 1 + 2( - |
m1+2) |
< |
^m |
1+2 |
< |
1 b m,+2(P |
m 1 + 21 |
1 bm1+m2 |
m1+m2 ) |
|
^m1 |
+m2 |
|
'bm1+m2 |
m1+m2) |
В общем матричном виде указанное уравнение можно записать:
la = Ga (0)Va + Ia (ст) Vb = Rb (a)lb + Eb (ст) Рассмотрим гибридное описание схемы:
133
ia
=
H
a a V
a +
Ha
b 1
b
+
Sa
V
=
Hbv
+
H
J b +
л
»
Т.к.
напряжения на входах и токи входов есть
не что иное, как напряжения и токи
нели-
нейных элементов, то можно
записать:
Ga
(G)Va
+
I
а
(°)" HV
~ H
J
b
~
~ = 0
Rb
(a)
Ib +
Eb
(а)-HbaVa -
H
J b -
Sb = 0
Как
и прежде, эти уравнения справедливы
при выполнении условий принадлежности
то-
чек выбранным отрезкам аппроксимации
нелинейных ВАХ. Обратим внимание также
на тот
факт, что I
a
(q)
и Eb(q)
константы для выбранных отрезков.
Таким
образом, подлежащие решению нелинейные
уранения пишутся в виде:
F
V
1
b
у
Ga
(a) -
Ha
-
H
H
Rb
(v) -
H>b
♦ '
■ (° " s = 0
Vb
(a) -
St
Вспомним
итерационную формулу метода Ньюона-Рафсоча:
=
_ j-iX у
(x
)
Рассмотрим
начальное приближение V°,
Ib,
которому соответствуют отрезки
а0. Тогда:
V1 |
|
VaP |
|
Ga (a°) -Haa} - Hab |
-1 |
Ga (a0) - Ha a \ - Hab |
Vе X а 11 |
II |
|
Ib0 |
|
/ОО \ ~ H b a Rb ( J-Hbb |
|
- H b a Rb (°°) - Hbb |
Ga (Я") - Ha --I-
H
ab
' I a(Q) " S
H
i Rb(v0) - H ь Vb (a) - Sh
Т.е. необходимо знать не точку Va, Ib, а лишь комбинацию отрезков. Аналогично
V"+1 |
|
V n |
|
a |
|
|
|
jn + 1 |
|
|
|
I b |
|
I I |
|
G a I - H a a |
\ - H a b |
-1 |
G a ) - H a a |
\ - H a b |
- H b a |
! Rb (*n) - Hbb |
|
- H b a |
! Rb (*n) - Hbb |
a \ ~ H a b |
Ia (Я") |
a |
|
|
|
Van |
X |
|
|
Ia ь n |
-H b a 1 Rb
(Я" ) - H
bb
Vb (*n) - Sb
ЗАДАЧИ.
2 (]) 1 1. Составить гибридную матрицу H для схемы рис. 3.57
-j — г — с с л - методом возбуждений-откликов.
vл п2 (1) П1 (2) @li2 2. Сделать 2 шага нахождения корня уравнения методом
ab
ba
a
Рис. 3.57
134
XX + 4x - 2 = 0 f XX - 4x + 2 = 0
3. Определить коэффициент абсолютной чувствительности модуля коэффициента пере- дачи интегрирующей RC-цепи на частоте ю к изменению параметров R и С.
135
