
- •Содержание 2
- •Введение. 136
- •2. Введение
- •1. Основные понятия
- •1.1 Моделирование. Основные понятия.
- •1.1.1 Системный анализ и моделирование
- •1.1.2 Концептуальные модели.
- •1.1.3 Термины и определения
- •1.1.4 Формализация и алгоритмизация процессов.
- •1.2 Математическое моделирование
- •1.2.1 Классификация математических моделей.
- •Классификация математических моделей на основе особенностей применяемого математического аппарата
- •1.2.2 Основной принцип классификации математических моделей
- •1.2.3 Программирование модели
- •1.2.4 Испытание модели
- •1.2.5 Исследование свойств имитационной модели.
- •Эксплуатация имитационной модели.
- •Анализ результатов моделирования.
- •1.3 Виды анализа и расчета электронных схем
- •1.4 Модели элементов и схем
- •2. Модели компонентов электронных схем
- •2.1 Классификация моделей
- •2.2 Интерполяция и аппроксимация функций при создании моделей
- •2.2.1 Интерполяция функций
- •2.2.2 Аппроксимация функций
- •2.3 Модели основных электронных компонентов
- •2.3.1 Базовый набор элементов моделей
- •2.3.2 1.1 Резистор
- •1. Пассивные компоненты и их модели
- •2.3.3 1.2 Конденсатор
- •2.3.4 Реальные конденсаторы
- •2.3.5 Катушка индуктивности и дроссель
- •2.3.6 Реальная индуктивность
- •2.3.7 Модели полупроводниковых приборов
- •2.4 Модели аналоговых компонентов программы Micro-Cap
- •2.4.1 Общие сведения о моделях компонентов
- •2.4.2 Пассивные компоненты
- •2.4.3 Резистор (Resistor)
- •Разброс сопротивления при использовании Monte-Carlo
- •3. Матрично-векторные параметры схем
- •3.1 Основные законы электрических цепей в матричном виде
- •3.2 Метод контурных токов
- •3.3 Метод узловых потенциалов
- •3.4 Метод обобщенных ветвей
- •3.5 Статический анализ линейных и нелинейных схем
- •3.6 Гибридный анализ электронных схем
- •4. Методы анализа переходных процессов
- •4.1 Введение
- •4.2 Литература
- •4.3 Основные задачи анализа переходных процессов
- •4.4 Анализ переходных процессов в линейных цепях
- •4.5 Анализ переходных процессов в нелинейных схемах и численные методы интегрирования нелинейных ду
- •4.5.1 Общие сведения о численных методах решения систем дифференциальных
- •4.5.7 Сведение расчета переходных процессов в электронных цепях к расчету цепей по постоянному току
- •4.6 Анализ переходных процессов в цепях с периодической
- •4.6.3 Дискретное преобразование Лапласа и его основные свойства
- •9. Теорема дифференцирования по параметру
- •10. Теорема интегрирования по параметру
- •11. Теорема об умножении изображений (теорема свертывания в вещественной области).
- •4.6.4 Решение линейных разностных уравнений
- •4.7 Параметрические цепи
TF=1+TC1-(T-
TNOM)+TC2-(T- TNOM)2.
Параметр
модели резистора TC1 —
линейный
температурный коэффициент, часто
задается в справочном листке резистора
как миллионные доли
на °C (ppm/degree C). Для
преобразования этого справочного
параметра в TC1 необходимо
его деление
на 1000000. Так,
например, справочный параметр 3000
ppm/degree C соответствует
значению TC1=3E-3.
Если
<имя модели>
указано и указан TCE, сопротивление
рассчитывается как
<со- npomueneHue>*TF,
но температурный фактор TF
определяется по экспоненциальной
формуле:
TF
=1 01 TCE(T-TNOM) .
Если
определено и
<имя модели>,
и |TC=<fc1>[,<fc2>]] в
строке атрибута
RESISTANCE,
то значения температурных
коэффициентов
в строке
RESISTANCE
[TC=<tc1>[,<tc2>]]
имеют приоритет.
Во
всех вышеприведенных формулах Т —
текущее значение температуры (указывается
по директиве .TEMP); TNOM
—
номинальная температура, равная по
умолчанию 27° С (указывается в окне
Global
Settings).
Допуски
LOT и DEV для
анализа Монте-Карло, доступны только
при определении <имени
модели> в
окне задания параметров или модельной
директивы .MODEL в текстовой
области или
на поле схемы. Допуски могут выражаться
в относительных (процентах) или
абсолютных единицах
и могут быть указаны для
всех параметров модели, за исключением
температурных параметров. Обе формы
задания допусков преобразуются в
эквивалентное процентное отклонение
и воздействуют на MF (фактор
Монте- Карло), который, в свою очередь
умножается на величину сопротивления
с учетом тем - пературных факторов.
MF=
1 ± <разброс в процентах DEV
или LOT>/100
Если
значение разброса в % (LOT или
DEV) равно нулю или анализ
по методу Монте-Карло не используется,
то MF-фактор устанавливается
в единичное значение и не воздействует
на окончательную величину сопротивления
резистора
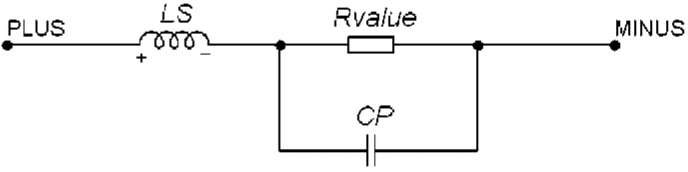
Rvalue
(рис. 5.4).
Рис.
5.4. Модель резистора Окончательно
сопротивление резистора
Rvalue
вычисляется по формуле:
Rvalue
= <сопротивление> R-TF-MF
Шумы
резистора
Резистору
свойственно напряжение шума, которое
возникает из-за неупорядоченного
теплового движения
носителей заряда. Спектральная плотность
теплового шумового тока резистора
рассчитывается по формуле Найквиста:
A
I
- N M ...14 • •
Rvalue
4hZ
62
C<umh>
<узел +> <узел -> [имя модели] ,,C1
+
[емкость]
[\С=<начальное напряжение>]
Пример: C2
C2
7
8 1 10P\C=2
.1m
C3
Атрибут
PART:
<имя>
— позиционное обозначение или произ-
+ 11
вольное имя компонента. 1
E-3
NM
представляет
собой масштабный коэффициент шумового
тока и является модельным параметром.
Установка его в нулевое значение
приводит к тому, что все резисторы,
имеющие заданную модель не вносят вклад
в общий шум схемы.
Примеры
задания резисторов и их атрибутов см.
в схемных файлах
resistors.cir,
re- sistorjreq.cir.
из
папки
Components\Passive
Comp
(book-mc.rar).
2.4.4
Конденсатор (Capacitor)
Формат
SPICE
Capacitor
Формат
схем Micro-Cap
(рис.
5.6)
Примеры: Рис.
5.5. УГО
C5 конденсатора
XC16
•
Атрибут
CAPACITANCE:
<емкость> [Ю^начальное напряжение>]
Если
<емкость>
определяется в виде выражения, содержащего
переменные состояния схемы, то это
выражение используется только при
анализе во временной области.
Например, выражение, записанное в
позиции
CAPACITANCE
1n+V(10)*2n, содержащее
значение потенциала узла 10, будет
использовано при анализе переходных
процессов, при расчете режима по
постоянному току перед выполнением
малосигнального частотного анализа
(AC),
и
при расчете передаточных характеристик
по постоянному току (DC).
В
режиме малосигнального частотного
анализа (AC)
зависимость
рассматриваемой емкости от потенциала
V(
10)
не принимается во внимание. Если в
рабочей точке по постоянному току
значение потенциала узла 10 оказалось
равным 2В, то емкость рассматриваемого
конденсатора во время проведения
частотного анализа будет равной
1n+2*2n=5n.
Ю=<начальное
напряжение>
— присваивает начальное значение
напряжению на конденсаторе. Примеры:
1U
110P
\C=3
50U*(1+V(6)/100)
1N/(1+V(C1)A2)
.
Атрибут
CHARGE:
[заряд]
Пример:
ATAN(V(C1))
Если
поле атрибута CHARGE
[заряд]
заполняется, то оно должно быть
выражением, включающем переменные
состояния схемы, такие как, например,
напряжение на конденсаторе и другие,
возможно символьные переменные,
определенные директивами (.define
или
.param).
63Разброс сопротивления при использовании Monte-Carlo
В
вИ . -л
. гл
й гу ж
11
№ • ав | as
l o B G л
I
•
JrJH
.
.. r
щщ:
si.
ii f
npgtrce
vs. Froany
I
1
F(Hb)
л]njx]
["■-K
UK 1CCK 1M КМ
КШ 1G
1CG 1CCG
I MODEL р Show |
Value | CAP_MOD_C1 л 5 h ™ ch a n 5 e | |
|
|
-Display 1 Pin Markers V Pin Names V Pin Numbers (7 Current W Power !•/ Condition Color |
|
ec m
COST = POWER=
5HAPEGROUP=Default
Urn
Font , I Add Delete | Browse,,. | Combinations |
IBIS,..
W Enabled Г Help Bar
So, tiT.: гг,- text aea of CMC£^C|LIVD9_Ff5i05_Mqde^D5_ne[o^E.Cna С 11 ЮГ=Ш, LS fiN RP fHEG
RS ~C2 TABS | undehed TVEABLffD | undefined
TRE1GOEAL | unde^ TRELJOCA. | unde^ tci fo
VC5, Ifr
Рис. 5.6. Окно задания параметров конденсатора
Правила использования выражений в полях атрибутов CHARGE и CAPACITANCE
Может быть использован любой из атрибутов [емкость] или [заряд].
Если заполнены поля обоих атрибутов и [емкость] и [заряд], пользователь должен гарантировать, что [емкость] — это производная от [заряда] по напряжению на конденсаторе, т.е. [емкость]=6[[заряд])Ш.
Если атрибут [емкость] не задан, а атрибут [заряд] задан, Micro-Cap создаст выражение для вычисления емкости путем взятия производной от заряда по напряжению: C=dQ/dV.
Если [емкость] задается в виде выражения C(V), и [заряд] не определяется, Micro- Cap создает эквивалентную схему, содержащую источник тока величиной C(V)*DDT(V). В этом случае, заряд конденсатора всегда будет равен нулю. Во всех других случаях, переменная заряда конденсатора Charge — доступна.
Если [заряд] определяется, выражение для него должно включать напряжение на конденсаторе. Даже для постоянной емкости, Q(C)=C*V(C).
Если [емкость] или [заряд] даются в виде выражений, зависящих от времени, атрибут MODEL игнорируется. Емкость и заряд определяются исключительно выражениями и на них не оказывают никакого влияния модельные параметры.
Атрибут FREQ: [<Р-выражение>].
Если в поле этого атрибута присутствует выражение, то оно при проведении AC- анализа заменяет значение емкости, рассчитанное в рабочей точке по постоянному току. Т.е. если в этой позиции набрано частотно-зависимое выражение, например 1n+1E- 9*V(1,2)*(1+1Cm*log(f)), то оно при проведении малосигнального частотного анализа (AC) заменяет значение атрибута CAPACITANCE. Например, в вышеприведенном выражении для атрибута FREQ F обозначает независимую переменную AC-анализа — частоту, a V(1,2) — малосигнальное напряжение между узлами 1 и 2. При расчете переходных процессов и передаточных характеристик по постоянному току емкость конденсата - ра будет определяться значениями атрибутов CAPACITANCE и CHARGE, независимо от наличия и значения атрибута FREQ.
Атрибут MODEL: [имя модели]
. Назначение остальных атрибутов COST, POWER, SHAPEGROUP, PACKAGE — аналогично ранее рассмотренным для резистора (см. 5.2.1).
*
Plot:AC Analysi
Capacitor
pedance vs F
/
Cancel
/
• j Syn
| Help
Single
64
Представленные
УГО конденсатора (рис. 5.5), показывают
разновидности значений атрибута
SHAPEGROUP:
C1 -
main;
C2 -
electrolytic;
C3
-
polarity.
Формат
текстовой директивы модели конденсатора
.MODEL
<имя модели>
CAP
([параметрымодели])
Параметры
модели конденсатора приведены в табл.
5.2.
Примеры:
.MODEL
CMOD CAP(C=2.0 L0T=10% VC1=2E-3 VC2=.0015)
.MODEL
CEL CAP(C=1.0
L0T=5%
DEV=.5% T_ABS=37)
Если
[имя модели]
задано и модельные параметры определены
тем или иным способом (в библиотеке
или текстовой директиве), то они
используются при анализе. Однако,
если при этом определен один из атрибутов
[емкость] или
[заряд]
в виде выражений, зависящих от времени,
тогда значение атрибута
MODEL
игнорируется.
Квадратичная
зависимость емкости от напряжения
Если
в окне атрибутов используется
[имя модели],
то значение, записанное в строке атрибута
CAPACITANCE
умножается
на QF-фактор
для вычисления емкости конденсатора,
зависящей от напряжения на его выводах:
QF
= 1+ VC1-V + VC2-V2
Эта
возможность оставлена в программе
Micro-Cap
для
сохранения совместимости с версией
языка SPICE
2G.
Температурная
зависимость емкости
Температурная
зависимость емкости подобна температурной
зависимости сопротивления, задается
значениями 2-х модельных коэффициентов
TC1
и
TC2.
В
случае задания
[имени модели]
в окне атрибутов,
<емкость>
в строке атрибута
CAPACITANCE
домножается
на значение TF-фактора,
который вычисляется по формуле:
TF
= 1+TC1-(T-Tnom)+TC2 (T-Tnom)2
Таблица
5.2.
Параметрымодели конденсатора
Обозначени е |
Содержание |
Размерн ость |
Значени е по умолчан ию |
с |
Масштабный множитель емкости |
|
1 |
LS |
Последовательная индуктивность |
Гн |
0 |
RP |
Параллельное сопротивление |
Ом |
да |
RS |
Последовательное сопротивление |
Ом |
0 |
VC1 |
Линейный коэффициент зависимости от напряжения |
в-1 |
0 |
VC2 |
Квадратичный коэффициент зависимости от напряжения |
в-2 |
0 |
65
2.4.5
Катушка индуктивности (Inductor)
Формат
SPICE
1<имя>
<узел +> <узел -> [имя модели]
+
[индуктивность] [Ю=<начальный ток>]
ПрИМерЬК Inductor
11
2 3
11U
L2
7
8 11CP
IC=2
ТС1 |
Линейный температурный коэффициент емкости |
°с-1 |
0 |
ТС2 |
Квадратичный температурный коэффициент емкости |
°с-2 |
0 |
T_MEASURED |
Температура измерения |
°С |
— |
T_ABS |
Абсолютная температура |
°С |
— |
T_RE L_G LO BAL |
Относительная температура |
°С |
— |
|
Разность между темпера |
|
|
T_REL_LOCAL |
турой устройства и модели- прототипа (AKO) |
°С |
— |
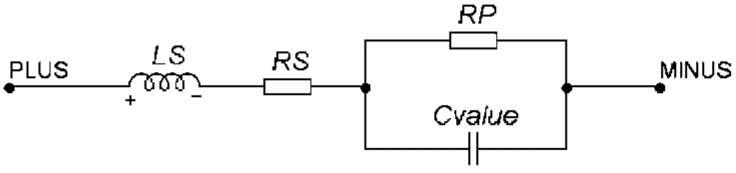
Рис. 5.7. Модель конденсатора Разброс емкости
Задается так же, как и разброс сопротивления в модельной строке с помощью ключевых слов LOT или DEV для любых параметров модели, за исключением температурных. В вычислении значения емкости учитывается домножением на MF-фактор, вычисляемый по формуле:
MF=1 ± <разброс в процентах DEV или LOT>/100
Окончательное значение емкости конденсатора при задании в окне атрибутов [имени модели] Cvalue (рис. 5.7) определяется выражением:
Суа1ие=<емкость> • C- QF- TF- MF= =<емкость> -С-(1 +VC-V+VC2- V2)[ 1+TC1(T-TNOM)+ TC2(T-TNOM) 2]MF.
Шумы конденсатора
Если заданы модельные параметры RS и RP, то указанные резисторы рассматриваются как источники теплового шума:
IRS =
4 • k • T RS
IRP =
4 • k • T RP
l 1 l2
л т п -
+30U" 1E-4 Рис. 5.8. УГО индуктивности
Формат схем Micro-Cap (рис. 5.9) Атрибут PART: <имй>
л
66
Примеры:
L5,
L1
Атрибут
INDUCTANCE
<индуктивность>
[1С=<начальныйток>]
Если
<индуктивность>
определяется в виде выражения, содержащего
переменные состояния схемы, то оно
используется только при анализе во
временной области. Например, выражение,
записанное в позиции INDUCTANCE
1U/(1+I(L2)A2),
содержащее
ток катушки L2,
будет
использовано при анализе переходных
процессов, при расчете режима по
постоянному току перед выполнением
малосигнального частотного анализа
(AC),
и
при расчете передаточных характеристик
по постоянному току (DC).
В
режиме малосигнального частотного
анализа (AC)
зависимость
рассматриваемой индуктивности от тока
I(L2)
не
принимается во внимание. Если в рабочей
точке по постоянному току значение
тока через катушку L2
оказалось
равным 2A,
то
рассматриваемая индуктивность во время
проведения частотного анализа будет
принята равной 1U/(1+2A2)=0.2U.
IC=<начальный
ток>
— присваивает начальное значение току
через катушку в режиме анализа
переходных процессов, если флажок
Operating
Point
сброшен.
Примеры:
1U
110U
IC=3
1U/(1+I(L2)A2)
Атрибут
FLUX:
[магнитный поток]
Пример:
1u*ATAN(I(L2))
При
задании атрибута
FLUX
должно
быть указано выражение, включающее
переменные состояния катушки, такие
как ток через нее и возможно, другие
символьные переменные,
определяемыедирективами .define
или
.param.
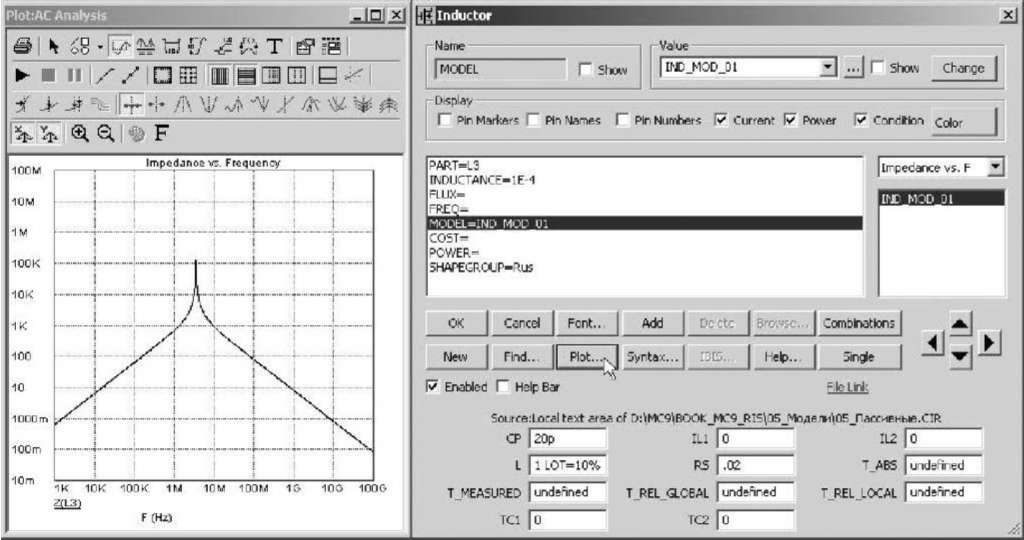
Рис.
5.9. Окно задания параметров катушки
индуктивности
Правила
использования выражений для атрибутов
FLUX и INDUCTANCE
Должно
быть задано хотя бы одно выражение
либо
[индуктивности]
либо для [магнитного
потока].
Если
заданы оба значения как
[индуктивности],
так и
[магнитного потока]
в виде выражений, зависящих от
времени, пользователь должен
гарантировать, что
[индуктивность]
является производной
[магнитного потока]
по току через катушку:
[индук- тивностьА([магнитный
nomoK])/d
I
67
Если
[индуктивность]
не задается, а
[магнитный поток]
представляет собой выражение,
зависящее от времени, Micro-Cap
создаст
выражение для индуктивности путем
дифференцирования магнитного
потока по току катушки: L=dX/dI.
Если
[индуктивность]
является выражением, зависящим от
времени, а
[магнитный поток]
не задается, Micro-Cap
создаст
эквивалентную схему для катушки,
состоящую из источника эдс величиной
L(I)*DDT(I).
Если
[магнитный поток]
представляет собой выражение, зависящее
от времени, то оно должно включать в
себя ток через катушку. Даже для
линейной катушки X(L)=L*I(L).
Если
[индуктивность]
или [поток] заданы выражением во
временной области, атрибут MODEL
не
принимается во внимание и катушка не
может быть связана с K-
сердечником,
т.е. обладать взаимной индуктивностью.
Индуктивность и поток определяются
исключительно выражениями во временной
области и на них не могут оказывать
влияние модельные параметры.
Выражение,
зависящее от времени, представляет
собой любое выражение, использующее
переменные, которые изменяются в течение
проведения моделирования, такие как
V(L1)
или
I(L2).
Атрибут
FREQ: [<F-выpaжeнue>].
Пример:
1.2mh+5m*(1+log(F))
Если
в поле этого атрибута присутствует
выражение, то оно при проведении AC-
анализа
заменяет значение индуктивности,
рассчитанное в рабочей точке по
постоянному току с помощью выражения
в поле атрибута
INDUCTANCE.
Т.е.
если в этой позиции набрано
частотно-зависимое выражение, например
10mh+I(L1)*(1+1E-9*f)/5m,
то
оно при проведении малосигнального
частотного анализа (AC)
заменяет
значение атрибута
INDUCTANCE.
Например,
в вышеприведенном выражении для атрибута
FREQ
F
обозначает
независимую переменную AC-анализа
— частоту, a
I(L1)
— малосигнальный ток через катушку
L1.
При
расчете переходных процессов и
передаточных характеристик по
постоянному току индуктивность будет
равна значению атрибута
INDUCTANCE
независимо
от наличия и значения атрибута
FREQ.
Атрибут
MODEL:
[имя модели]
.
Назначение остальных атрибутов
COST,
POWER, SHAPEGROUP, PACKAGE
—
аналогично ранее рассмотренным для
резистора (см. 5.2.1).
Представленные
УГО катушки индуктивности (рис. 5.8),
показывают разновидности значений
атрибута
SHAPEGROUP:
L1 -
main;
L2 -
Rus
(доработка
авторов). Формат
текстовой директивы модели индуктивности
.MODEL
<имямодели>
IND
([параметрымодели])
Примеры:
.MODEL
LMOD IND (L=2.0 LOT=10% IL1=2E-3 IL2=.0015)
.MODEL
L_W IND (L=1.0 LOT=5% DEV=.5% T_ABS=37)
Параметры
модели индуктивности приведены в табл.
5.3.
Если
в окне атрибутов катушки
[имя модели]
опущено, то её индуктивность равна
<индуктивности>
в Генри, записанному в строке атрибутов
INDUCTANCE.
В
противном случае индуктивность
вычисляется умножением на масштабный
коэффициент индуктивности L
ина
коэффициенты факторов, перечисленных
ниже.
68
Квадратичная
зависимость индуктивности от тока
Если
в окне атрибутов используется
[имя модели],
то значение, записанная в строке атрибута
INDUCTANCE
умножается
на QF-фактор
для вычисления индуктивности катушки,
зависящей от тока в ней:
QF
= 1+ IL1-I + IL2-I2
Эта
возможность оставлена в программе
Micro-Cap
для
сохранения совместимости с версией
языка SPICE
2G.
Температурная
зависимость индуктивности
Температурная
зависимость индуктивности подобна
температурной зависимости со - противления
и емкости (см. 5.2.1, 5.2.2). Задается значениями
двух коэффициентов — TC1
и
TC2.
В
случае задания
[имени модели]
в окне атрибутов,
<индуктивность>
в строке атрибута
INDUCTANCE
домножается
на значение TF-фактора,
который вычисляется по формуле:
TF=1+TC1
•(T-Tnom)+TC2-(T-Tnom)2 Таблица
5.3.
Параметры модели индуктивности
Обозначение |
Содержание |
о X о Го о CL |
S X О 3- с ш о > |
L |
Масштабный множитель индуктивности |
|
1 |
CP |
Параллельная емкость |
Ф |
0 |
RS |
Последовательное сопротивление |
Ом |
0 |
IL1 |
Линейный коэффициент зависимости от тока |
А-1 |
0 |
IL2 |
Квадратичный коэффициент зависимости от тока |
А-2 |
0 |
TC1 |
Линейный температурный коэффициент индуктивности |
° с - 1 |
0 |
TC2 |
Квадратичный температурный коэффициент индуктивности |
° с - 2 |
0 |
T_MEASURED |
Температура измерений |
° с |
— |
T_ABC |
Абсолютная температура |
° с |
— |
T_RE L_G LO BAL |
Относительная температура |
° с |
— |
T_REL_LOCAL |
Разность между температурой устройства и модели-прототипа (AKO) |
° с |
— |
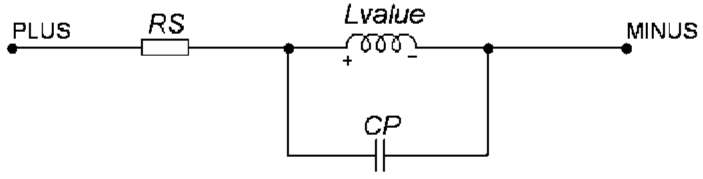
Рис. 5.10. Модель катушки индуктивности
69
2.4.6 Взаимная индуктивность и магнитный сердечник (К) Формат SPICE
К<имя> L<umh катушки> <L<umh катушки»* коэффициент связи> К<имя> L<umh катушки>* коэффициент связи> <имя модели> Примеры:
K1 L1 L2 .98
K1 L1 L2 L3 L4 L5 L6 .999 Формат схем Micro-Cap (рис. 5.12, 5.13) Атрибут PART: <имя> Пример: K1
Атрибут INDUCTORS: <имя катушки> <имя ка- Пример: L1 L2 L3
к
AeeeeAki
MODEL=
t= ===± K2
MODEL=N97
уго
Из-за наличия паразитных параметров частотная характеристика катушки индуктивности может иметь резонансный пик (см. рис. 5.9).
Разброс индуктивности
Задается так же, как и разброс сопротивления в модельной строке с помощью ключевых слов LOT или DEV для любых параметров модели, за исключением температурных. При расчете значения индуктивности учитывается умножением на MF-фактор, вычисляемый по формуле:
MF=1 ± <разброс в процентах DEV или LOT>/100
Окончательное значение индуктивности катушки Lvalue (рис. 5.10) при задании в окне атрибутов [именимодели] определяется выражением:
Lvalue = < индуктивность>- L- QF- TF-MF= =<UHdyKmu6H0cmb>L(1+IL1-I+IL2-I2)[1+TC1(T-TNOM)+TC2-(T-TNOM)2]-MF.
Шумы катушки индуктивности
Если в параметрах модели задано паразитное последовательное сопротивление RS, то оно рассматривается как источник теплового шума, задаваемый в виде спектральной плотности шумового тока:
IR.S
V RS
рис
тушки>*
магнитного
сердечника
Атрибут COUPLING: <коэффициент связи> Пример: 0.99
Атрибут MODEL: [имя модели] Пример: K_3C8
Порядок перечисления имен индуктивностей Lyyy, Lzzz ... не имеет значения, знак взаимной индуктивности определяется положительными направлениями токов индуктивностей относительно начал обмоток. Параметром взаимной индуктивности является коэффициент связи.
На одном сердечнике помещается одна или несколько обмоток с именами Lyyy, Lzzz... Все обмотки имеют одинаковое значение коэффициента связи>. При хорошей магнитной связи, осуществляемой посредством замкнутого ферромагнитного сердечни
70
ка,
величина коэффициента связи находится
в пределах 0.98...0.999. Единичное значение
коэффициента связи соответствует
100%-ной магнитной связи между обмотками,
что является эквивалентом отсутствия
индуктивностей рассеивания. При задании
магнитной связи возможны 2 варианта:
магнитосвязанные
индуктивности линейны;
магнитосвязанные
индуктивности нелинейны (имеется
нелинейный магнитный сердечник,
определяемый моделью типа CORE).
Выбор
нелинейного или линейного магнитного
сердечника зависит от моделируемо - го
электронного устройства. Если нелинейные
явления в сердечнике (гистерезис и
насыщение) являются принципиальными
для работы устройства (например, в
ключах на магнитных усилителях и
магнитных реакторах), то используется
нелинейный сердечник, если же — нет,
(например импульсный или сетевой
трансформатор), то используется линейный
сердечник.
Магнитосвязанные
линейные индуктивности.
Если
при описании взаимной индуктивности
и магнитного сердечника К (рис. 5.12) не
задан атрибут
MODEL,
то
расчеты проводятся для линейных
индуктивностей.
Рис.
5.12. Окно задания параметров линейного
сердечника Коэффициент связи Ki/
двух
обмоток
(i,
j)
определяется
выражением
м„
к
где
U,
Lj —
индуктивности обмоток; Mj
—
их взаимная индуктивность.
Напряжение
на катушке L,
с
учетом взаимной индукции определяется
выражением:
Ui
= +ы/-А+м,А+...,
dt
dt dt
где
h
—
ток, втекающий в вывод (+) обмотки (помечен
на схеме точкой).
В
этом случае при вводе в схему связанных
индуктивностей посредством вставки
элемента K,
в
открывающемся окне параметров задается
лишь позиционное обозначение
сердечника KN,
позиционные
обозначения всех катушек индуктивности
(INDUCTORS)
с
которыми он связан и коэффициент связи
(COUPLING)
(см.
рис. 5.12).
71
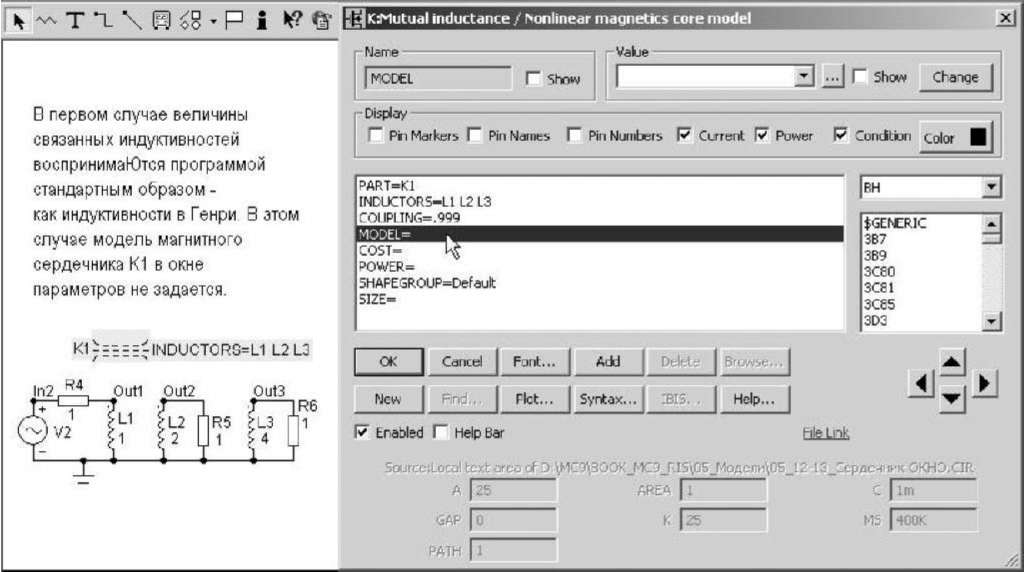
Рис.
5.13. Окно задания параметров нелинейного
сердечника
Следовательно,
в случае использования нелинейного
магнитного сердечника, вели-
чина,
задаваемая в позиции
INDUCTANCE
катушки
индуктивности, не может быть выра-
жением,
а должна быть целым положительным
числом.
Параметры
модели магнитного сердечника приведены
в табл. 5.4.
Таблица
5.4.
Параметры модели магнитного сердечника
Магнитосвязанные
катушки с нелинейным магнитным
сердечником
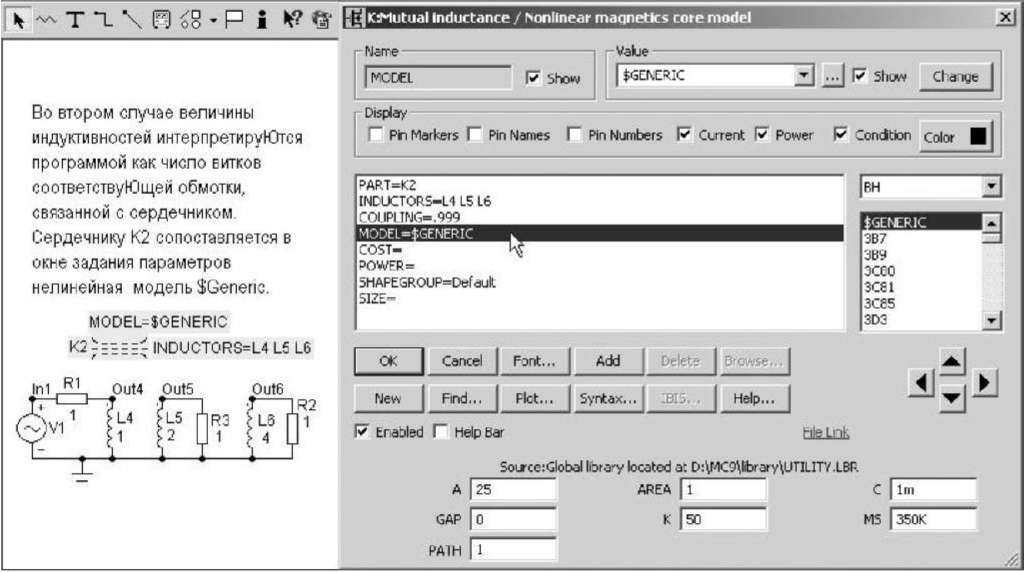
Если
при описании взаимной индуктивности
и магнитного сердечника К (рис. 5.13) задан
атрибут
MODEL
(указана
модель сердечника), то расчеты проводятся
для нелинейных индуктивностей.
Следует
обратить внимание, что при этом изменяется
смысл параметра
<индуктивность>
для магнитосвязанных катушек индуктивности
Lxxx,
перечисленных
в поле параметра INDUCTORS.
Теперь
при описании каждой обмотки Lxxx
численное
значение, задаваемое в позиции INDUCTANCE
окна
параметров катушки индуктивности
определяет не индуктивность, а число
витков соответствующей обмотки
сердечника.
Обознач ение |
Содержание |
Разм ер- ноет ь |
Значени е по умолчан ию |
AREA |
Площадь поперечного сечения магнитол ровода |
см2 |
1 |
PATH |
Средняя длина магнитной силовой линии |
см |
1 |
GAP |
Ширина воздушного зазора |
см |
0 |
MS |
Намагниченность насыщения |
А/м |
400-103 |
A |
Параметр формы безгистерезисной кривои намагничивания |
А/м |
25 |
С |
Постоянная упругого смещения доменных границ |
|
0.001 |
К |
Постоянная необратимой деформации доменных стенок |
А/м |
25 |
72
Список
связанных индуктивностей в окне задания
параметров сердечника может включать
даже единственную катушку.
Пример
задания и моделирования магнитосвязанных
катушек с линейным и нелинейным
сердечниками см. в схемном файле
Core3.cir
из
каталога
Components\Passive
Comp
(book-mc.rar).
Формат
текстовой директивы модели сердечника:
.MODEL
<имя модели>
CORE
(параметрымодели)
Примеры:
.MODEL
K1 CORE (Area=2.54 Path=.54 MS=2E5)
.MODEL
K2 CORE (MS=2E5 LOT=25% GAP=.001)
Особенности
модели магнитного сердечника
В
Micro-Cap
в
качестве модели магнитного сердечника
используется модель Джилса- Атертона,
которая не учитывает изменение параметров
магнитного сердечника в зависимости
от частоты (более подробно см. в 11.1). В
этой модели петли гистерезиса для
разных уровней перемагничивания
магнитного материала (значений Hm),
базируются
на безгистерезисной кривой, которая
строится в предположении отсутствия
эффектов деформации и вращения
векторов намагниченности доменных
структур ферромагнетика. Сами же
гистерезисные зависимости
M(H)
или
B(H),
получаются
на основе этой кривой с использованием
дифференциального уравнения процесса
(аналогичного сухому трению в механике),
характеризующегося постоянной
коэрцитивной силы K.
Параметры
модели магнитного сердечника имеют
сложную и далеко не очевидную связь со
справочными параметрами реальных
магнитных материалов. Для расчета
параметров модели используется
пункт меню
MODEL.
Для
выяснения влияния параметров модели
магнитного сердечника A,
K, C на
кривую петли гистерезиса можно
загрузить пример
core.cir
из
каталога
Components\Passive
Comp
(book-mc.rar) и
запустить анализ переходных процессов.
Затем можно организовать многовариантный
анализ при изменении модельных
параметров. Влияние увеличения
каждого модельного параметра представлено
в табл. 5.5:
Таблица
5.5.
Качественная оценка связи физических
параметров сердечника и параметров
модели
Параметр |
М |
HC |
BR |
A |
- |
+ |
+ |
K |
|
+ |
+ |
C |
+ |
- |
- |
В таблице у — дифференциальная магнитная проницаемость; HC — величина коэрцитивной силы; BR — величина остаточной индукции.
Построение графиков напряженности поля H и магнитной индукции B
В окне задания параметров анализа переходных процессов (Transient Analysis Limits) в графе Y expression можно задавать построение графиков магнитных величин в сердечнике следующим образом:
B(L1) — построение графика зависимости индукции B в сердечнике катушки L1 в единицах системы СГС (гаусс);
73
H(L1) — построение графика зависимости напряженности магнитного поля H в сердечнике катушки L1 в единицах системы СГС (эрстед);
BSI(L1) — построение графика зависимости индукции B в сердечнике катушки L1 в единицах системы СИ (тесла);
HSI(L1) — построение графика зависимости напряженности магнитного поля H в сердечнике катушки L1 в единицах системы си (A/m).
74
