
- •Содержание 2
- •Введение. 136
- •2. Введение
- •1. Основные понятия
- •1.1 Моделирование. Основные понятия.
- •1.1.1 Системный анализ и моделирование
- •1.1.2 Концептуальные модели.
- •1.1.3 Термины и определения
- •1.1.4 Формализация и алгоритмизация процессов.
- •1.2 Математическое моделирование
- •1.2.1 Классификация математических моделей.
- •Классификация математических моделей на основе особенностей применяемого математического аппарата
- •1.2.2 Основной принцип классификации математических моделей
- •1.2.3 Программирование модели
- •1.2.4 Испытание модели
- •1.2.5 Исследование свойств имитационной модели.
- •Эксплуатация имитационной модели.
- •Анализ результатов моделирования.
- •1.3 Виды анализа и расчета электронных схем
- •1.4 Модели элементов и схем
- •2. Модели компонентов электронных схем
- •2.1 Классификация моделей
- •2.2 Интерполяция и аппроксимация функций при создании моделей
- •2.2.1 Интерполяция функций
- •2.2.2 Аппроксимация функций
- •2.3 Модели основных электронных компонентов
- •2.3.1 Базовый набор элементов моделей
- •2.3.2 1.1 Резистор
- •1. Пассивные компоненты и их модели
- •2.3.3 1.2 Конденсатор
- •2.3.4 Реальные конденсаторы
- •2.3.5 Катушка индуктивности и дроссель
- •2.3.6 Реальная индуктивность
- •2.3.7 Модели полупроводниковых приборов
- •2.4 Модели аналоговых компонентов программы Micro-Cap
- •2.4.1 Общие сведения о моделях компонентов
- •2.4.2 Пассивные компоненты
- •2.4.3 Резистор (Resistor)
- •Разброс сопротивления при использовании Monte-Carlo
- •3. Матрично-векторные параметры схем
- •3.1 Основные законы электрических цепей в матричном виде
- •3.2 Метод контурных токов
- •3.3 Метод узловых потенциалов
- •3.4 Метод обобщенных ветвей
- •3.5 Статический анализ линейных и нелинейных схем
- •3.6 Гибридный анализ электронных схем
- •4. Методы анализа переходных процессов
- •4.1 Введение
- •4.2 Литература
- •4.3 Основные задачи анализа переходных процессов
- •4.4 Анализ переходных процессов в линейных цепях
- •4.5 Анализ переходных процессов в нелинейных схемах и численные методы интегрирования нелинейных ду
- •4.5.1 Общие сведения о численных методах решения систем дифференциальных
- •4.5.7 Сведение расчета переходных процессов в электронных цепях к расчету цепей по постоянному току
- •4.6 Анализ переходных процессов в цепях с периодической
- •4.6.3 Дискретное преобразование Лапласа и его основные свойства
- •9. Теорема дифференцирования по параметру
- •10. Теорема интегрирования по параметру
- •11. Теорема об умножении изображений (теорема свертывания в вещественной области).
- •4.6.4 Решение линейных разностных уравнений
- •4.7 Параметрические цепи
Здесь
сделано допущение о том, что
Rc>>rc,
что справедливо на высоких частотах
практически
всегда. Сопротивление
утечки
RC
учитывается, как правило, лишь в
прецизионных схемах и при расче-
те
медленных процессов. Зависимость
Zc(f)
в соответствии с приведен-
ным
соотношением имеет вид (рис. 1.12):
Таким
образом, после резонансной частоты f
= л сопро-
2
W
L
C
C
C
тивление
конденсатора приобретает индуктивный
характер. Следует от-
метить,
что для электролитических (оксидных)
конденсаторов величина Рис. 1.12.
емкости
непостоянна и существенно зависит от
частоты переменной составляющей
напряжения, при-
ложенного к
конденсатору. что объясняется процессами
поляризации диэлектрика. Для этих
конденса-
торов снижение емкости с
ростом частоты наблюдается, начиная с
сотен герц. Можно предложить ап-
проксимацию
зависимости
Cc(f)
в виде:
С
Полное
сопротивление конденсатора зависит
от частоты и определяется по формуле:
1
Л2
Z
с
=
Гс2
т+ +
a>Lr
coCr
с
1
+
f
У
'0 j
где
C0 - номинальная
емкость конденсатора, f0
- частота, на которой емкость падает
вдвое, а - некоторый коэффициент,
учитывающий скорость спада емкости.
У
электролитических (оксидных) конденсаторов
важным параметром является эквивалентное
последовательное сопротивление
(ERS).
Отсутствие учета этого параметра
в моделях конденсаторов, которые
используются в фильтрах выпрямителей
и в импульсных источниках питания,
может привести к неверным результатам
при моделировании этих устройств.
У
керамических конденсаторов емкость
также может существенно меняться в
зависимости от приложенного
постоянного напряжения. Зависимости
емкости от напряжения приводятся в
справочных данных на конденсаторы,
поэтому, в принципе, при построении
точной модели керамического конденсатора
необходимо учитывать эту нелинейную
зависимость.
Идеальная
катушка индуктивности характеризуется
потокосцеплением, возникающим при
протекании тока через некоторый
контур, причем считается, что активное
сопротивление контура равно 0. Отношение
потокосцепления ктоку называется
индуктивностью L:
L
= *
Размерности
величин: [i]=A,
[¥]=Вб=В-с, [Ц=Вб/А=(В-с)/А=Гн Энергия,
накопленная в поле: W
Wм
Закон
электромагнитной индукции связывает
скорость изменения магнитного потока
и эдс, наводимую в контуре:
e
=
dt
Если
L=const,
то e = L —
dt
Закон
можно переписать в другом виде:
л
39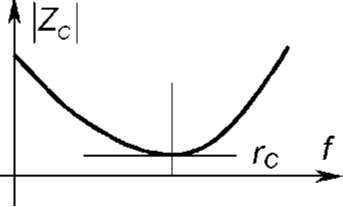
2.3.5 Катушка индуктивности и дроссель
i(t)
=
i(0) +
—
j
e(t )dt
V)
Реактивное
сопротивление контура переменному
току зависит от частоты синусоидального
сигнала: | Xl
| = coL .
Фазовый сдвиг между током и напряжением
— 90° Ток отстает от напряжения на
указанный угол. Если на индуктивность
подано напряжение: u
= Um
cosat,
при этом ток в цепи:
Мощность,
циркулирующая в цепи
P
=
u
L
cm
j- -
л L dl
В
обмотке за счет протекания тока создается
напряженность
магнитного поля H,
определяемая по закону полного
тока:
i
• w A
H
] =
coL
sin
cot
U
2 ■
л.
, U
2
■ о i
= sin
At
cos at =
sin
2a>t coL 2a>L
Таким
образом, мощность не потребляется
на-
грузкой, а осуществляется лишь
периодический об-
мен энергией (рис.
1.6):
Рис.
1.6. Временные диаграммы гармонического
сигнала на индуктивности
L
rL
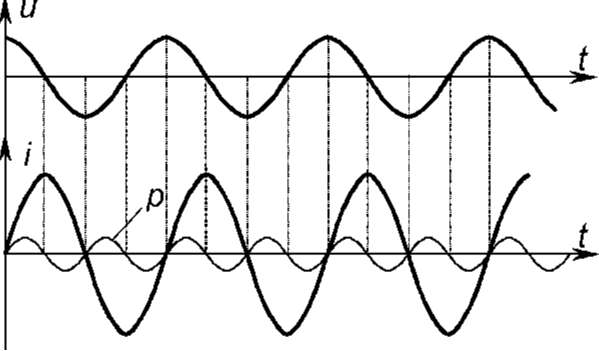
Рис.
1.13. Эквивалентная схема катушки
индуктивности
Катушка
индуктивности представляет собой
магнитопровод с выполненной на нем
обмоткой. Провод обмотки обладает
сопротивлением. Эквивалентная схема
индуктивности с учетом омического
сопротивления обмотки имеет вид
рис
Л1
3 :
Полное
сопротивление
такой катушки
индуктивности
переменному
току частотой
о равно:
Z
=
rL
+
ja>L
Z
=
+
(g)L
)2
. На высоких частотах необходим также
учет паразитной емкости (межвитковой
и межслоевой).2.3.6 Реальная индуктивность
|
|
|
|
R |
|
Особенно следует отметить особенности модели катушек индуктивности (дросселей), выполненных на сердечнике из ферромагнитного материала. Индуктивность такой катушки (дросселя) как правило, нелинейна при работе в сильных полях. Ее характеристика совпадает с магнитной характеристикой ферромагнетика и может быть изображена в виде графика (см. рис. 1.14). Кроме того, часто необходимо учитывать явление гистерезиса в сердечнике ферримагнитного метериала.
Если на индуктивность подан постоянный подмагничивающий ток lo , то можно выделить дифференциальную индуктивность Ld и статическую индуктивность Lcm определяемую выражениями:
i • w = H • / л h =
l
м
То |
7 |
Lcm j |
|
lo |
|
Если магнитная проницаемость материала д, то величина индук-
7 Гн
ции в сердечнике B = jujuoH, где juo = 4п • 10 —. Для торой
м
Рис. 1.14.
дального сердечника в предположении равномерного распределения магнитного поля справедливо:
с
40
где
lcp
- средняя длина магнитной силовой
линии, равная по-
лусумме внешнего
и внутреннего диаметра кольца, умноженная
на
п. При этом индуктивность
тороидального сердечника с обмоткой
можно
рассчитать по формуле:
L
: jujuoSw2
1
ср
Магнитную
характеристику материала обычно
аппроксимируют
кусочно-линейной
функцией при грубом расчете (см. рис.
1.15). При этом в диапазоне:
Be
H
Такая
аппроксимация является весьма грубой,
в частности, она не отражает реальных
физических
процессов во второй
области. Ведь, даже если предположить,
что в области насыщения свойства
фер-
ромагнетика исчезают вовсе, то
это означает, что д ферромагнетика
становится равной 1. Т.е. при
I
H
>Hs
магнитный поток необходимо считать
по формуле:
B
= M оH;
Это
соответствует аппроксимации (рис. 1.15,
линия 2). В ряде случаев оказывается
более удобной
аппроксимации магнитной
характеристики аналитическим выражением
вида:
B
=
Bs
•
thpH;
где
коэффициент р выражает «крутизну» и
момент перегиба магнитной характеристики.
Переменная
величина индуктивности может привести
к различию переходных процессов в
схемах,
если сердечник работает с
подмагничиванием или без него. Ряд
магнитных материалов обладает
гис-
терезисными свойствами, которые
проявляются в том, что кривая намагничивания
превращается в
петлю, которая зависит
от напряженности поля перемагничивания
H, скорости
и амплитуды Bm
индук-
ции в сердечнике. Существует
ряд моделей, описывающих эту петлю.
Одна из них - модель Джилса-
Аттертона,
используется в модели нелинейного
сердечника программы схемотехнического
моделиро-
вания Micro-Cap.
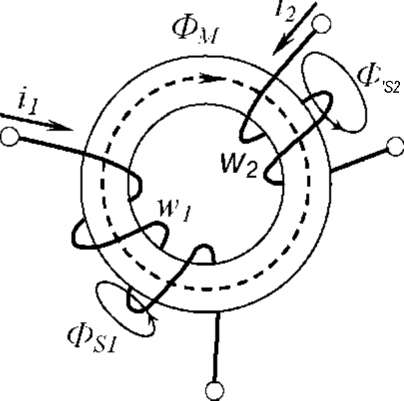
Трансформатор
Представляет
собой магнитопровод, на котором
вы-
полнены 2 или более обмотки (рис.
2.19).
По
магнитопроводу замыкается магнитный
поток
Фм,
который
обеспечивает магнитную связь между
обмотками.
Существуют потоки рассеяния
0
s
1
и 0s2,
создаваемые то-
ками ij,
и 12,
не замыкающиеся по магнитопроводу и
не яв-
ляющиеся общими для обмоток.
Обмотки имеют омические
сопротивления
rj
и Г2,
а также другие паразитные парамет-
ры,
например, межвитковые и межобмоточные
емкости.
Рис.
2.19 Идеальный
трансформатор представляется элемен-
том,
в котором отсутствуют потоки рассеяния,
активные сопротивления обмоток,
паразитные
емкости. Индуктивность
намагничивания равна бесконечности,
т.е. ток намагничивания равен
0. При
этом обмотки пронизывают одинаковые
потоки и по закону электромагнитной
индукции
для обеих обмоток можно
записать, что:
'M
dt
dt
dt dt
Здесь
n -w
2
/w
j
— коэффициент трансформации
трансформатора
B |
2, |
|
Bs |
|
H |
|
Hs |
|
W = BSw;
H
i • w
cp
cp
di + d;
2
Рис. 1.15.
-Hs <H < + H s, L
при H > H e L = 0, т.е. B = Bc
= Ex
w,
d 0 ,м
dy
U2 = e2 =
d0
w.
w w
= e1n
l
n
M
M
U
41
L
я-
i2-n
!
Из
закона сохранения энергии следует,
что:
\1 \2-n ~\2 \
e1 ei-n ii
"i i2
"2, т-е-
\2
-
2
n
Это
же вывод можно получить, используя
закон
Рис.
2.20 полного
тока с учетом того обстоятельства, что
\м-0:
X
w = 0;
i
2 • w 2 '
При
указанных допущениях трансформатор
можно представить эквивалентной схемой,
изображенной на рис. 2.20:
Модель
крайне проста, однако применяется
крайне редко, т.к. не позволяет учесть
принципиально важных для трансформатора
явлений — накопления энергии в
магнитопроводе и необходимость
восстановления магнитного состояния
сердечника. Для ее учета представляют
трансформатор совершенным элементом,
в котором отсутствуют потоки рассеяния,
но имеется конечная величина индуктивности
намагничивания L\
Последняя определяет ток
намагничивания, протекающий по
первичной обмотке, и приводит к
эквивалентной схеме в виде рис. 2.21:
В
ряде случаев, особенно при расчете
достаточно простых цепей, представляется
удобным «привести» трансформатор
к одной из сторон: первичной или
вторичной, представив процесс
передачи энергии через магнитопровод
непосредственным подключением нагрузки
к цепи источника энергии. Если, например,
трансформатор нагружен на активное
сопротивление R,
то
величина
тока нагрузки в первичной цепи
определится:
Щ
рТ
n
'12
'2 '
n
R
'
Тогда
эквивалентное сопротивление нагрузки,
подключенной к первичной цепи, равно:
eI
R
_ Щ_ _
U1-..R2
,2
U2
• n
R
Рис.
2.21
Несложно
показать, что индуктивность, включенная
в качестве нагрузки, приводится к
первичной стороне в виде:
Ь
- Ьг
Ь
- n2
Емкость
— в соответствии с
соот-
ношением:
с:
\i
U1
ЬЛ
R2'=R2/n2
C\' = C\-n2
L2'-L2/n2
Рис.
2.22
Таким
образом; эквивалентная схема «приведенного»
к первичной обмотке трансформатора
имеет вид (рис. 2.22).
Выполнение
трансформатора с сердечником из
магнитопровода в виде ферромагнетика
приводит к нелинейной зависимости
L(\).
Совершенная
эквивалентная схема трансформатора с
учетом Lм позволяет учесть важнейшую
особенность его — необходимость
восстановления исходного магнитного
состояния сердечника. Так, с учетом
приведенной выше эквивалентной схемы,
можно показать, что пода-
2
2
2
2
42![]()
