Point 3. Order reducing second order differential equations
1. Second order differential equation resolved with respect to the higher derivative if the right member of the equation depends only on the independent variable
.
(
22 )
One finds the general solution of this equation by twice integration, namely
( 23 )
■
.■
Note 7. If it is a matter of Cauchy problem for the equation (22) with initial conditions
then
it is well to integrate over an interval
,
namely
.
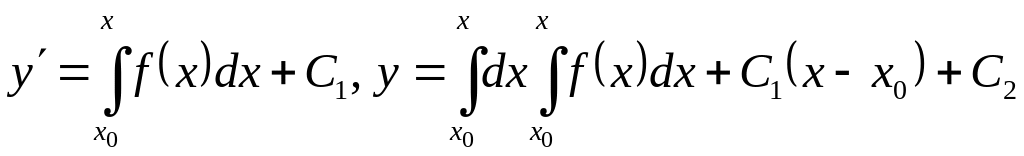In this case we at once have
,
and the solution of Cauchy problem takes on the next form
.
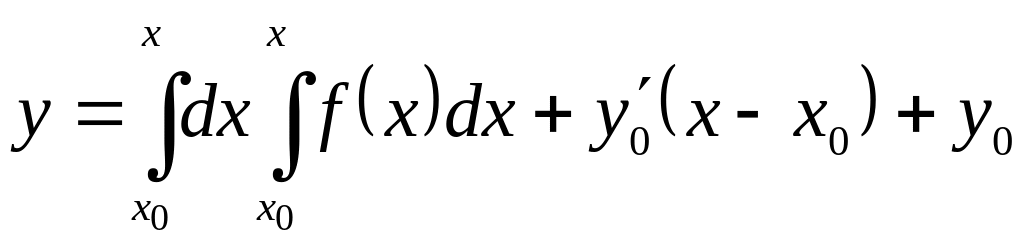Ex. 16. Solve the next Cauchy problem
Twice integrating we at first have the general solution of the differential equation,
.
Taking
into account the initial conditions we find
,
.
Therefore the solution of Cauchy problem
.
2. Second order differential equation not containing explicitly the unknown function
(
24 )
reduces to the first order differential equation by introducing a new unknown function
.
( 25 )
So long as
,
the equation (24) passes to the next one
.
( 26 )
We’ve got the first order differential equation
in
.
Suppose that we’ve found the general solution of the equation (26) of the form
.
In this case we can finish integration of the given equation as follows
.
Ex. 17. Find the general solution of the second order differential equation
.
This equation doesn’t contain explicitly the unknown function.
The first step. Putting
we get the first order linear equation in
,
.
By corresponding theory we put
and so
,
.
The second step. Returning to we find the general solution in question,
.
3. Second order differential equation not containing explicitly the independent variable
(
27 )
reduces to the first order differential equation by introducing an auxiliary unknown function
(
28 )
Differentiating a composite function we obtain
,
( 29 )
and so
.
( 30 )
We get the first order differential equation in
.
If we can find the general solution of the equation (30) in the next form
then
.
Ex. 18. Solve Cauchy problem for an equation
with initial conditions
.
The equation doesn’t contain explicitly the independent variable, and so we put
.
The first step.
;
by initial conditions
.
The second step.
.
On
the base of the first initial condition
,
and the solution of Cauchy problem is given by the equality
.
Ex. 19. Solve Cauchy problem
.
The first step.
.
By
virtue of initial conditions
(verify!) and so (after division by
)
.
This last differential equation is Bernoulli one, and we find its solution of the form
,
whence
.
;
;
from the initial conditions
,
.
The second step.
;
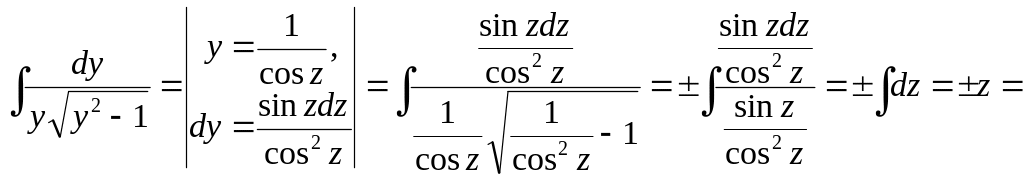
The required solution of Cauchy problem
or
.