3. Homogeneous de-1
Def. 11. The first order differential equation is called homogeneous one (with respect to the variables x, y) if it can be represented in the next form
.
(
15 )
Theorem 4. Homogeneous differential equation (15) as a rule reduces to that separable by introducing a new unknown function
.
(
16 )
■Finding and substituting its value in the equation we have
.
The
obtained equation is a separable one provided
.
Indeed, in this case
.■
Note 6. It can be proved that differential equation
,
( 17 )
is that homogeneous if for any
.
A more general differential equation
( 18 )
is homogeneous one if for any there exists a number k such that simultaneously
and
.
Prove these assertions yourselves.
Ex. 9. Solve Cauchy problem
.
Let’s divide both sides of the equation by x. We’ll get an equation of the form (15) that is a homogeneous equation,
,
because
of its right side is a function of the ratio
.
Acting by the theory we have
.
The initial condition gives
.
The solution of Cauchy problem
or
.
Ex. 10. Find the general solution of a differential equation
.
The given equation is that homogeneous because of for any
.
To prove homogeneity of the equation directly we rewrite it in the next form
and
then divide the numerator and denominator by
.
The right side of the equation is a function of the ratio , and so the equation is homogeneous one. By the theory we have
Ex. 11. Find a curve through a point
if the subtangent at its arbitrary point
equals the sum of coordinates of this point.
It
follows from the conditions of the problem that an unknown curve
can’t intersect the Ox-axis
and so lies above of this axis.
Let
is an equa-tion of a curve in question,
and
be the segments of the tangent and normal to the curve at its
arbitrary point
respectively, and
(see
fig. 2) . Then directed segments
and
are called respectively the subtangent and
Fig. 2 subnormal to the curve at
the point
.
For the case
(see fig. 2, where the point A lies
from the left of the point N)
.
We
can prove this from the right triangle
,
namely
;
the
same value of
we’ll
get proceeding from the equation of the tangent to the unknown curve
at the point
.
Indeed, the equation of the tangent is
If
we put
here, we’ll obtain
.
The length of the subtangent equals
,
and by the conditions of the problem we get the differential equation
with an initial condition
that is we have to solve Cauchy problem.
The first case
.
To determine the type of the equation we write it as follows
and divide the numerator and denominator of the fraction by x,
.
We get a differential equation of the form (15), and therefore it’s homogeneous one. Integrating it by corresponding method we have
.
The value of C we find by virtue of the initial condition. Substituting 0 for x and 1 for y in the general solution we get
.
The curve in question has the next equation:
or
.
The second case
.
Integration of the differential equation (which is also homogeneous one) gives
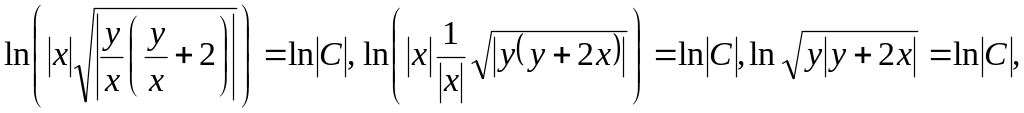
The initial condition is fulfiled only for
:
,
and therefore the curve in question is given by the equation
.
Answer. There are two solutions of the problem: , .