Point 2. Improper integrals
Improper integrals of the first kind
Def. 1. Let a
function
is continuous on an interval
.
If there exists a finite limit
( 6 )
then we say that the next integral (an improper integral of the first kind, an integral with infinite upper limit)
(
7 )
converges (exists, is convergent).
Thus by the definition 1
.
( 8 )
Def. 2. If the limit (6) is infinite one or doesn’t exist we say that the improper integral (7) diverges (doesn’t exist, is divergent).
By the same way we can define the next two improper integrals of the first kind
Def. 3.
(
9 )
if
a function
is
continuous on an interval
.
Def. 4.
.
( 10 ) if a function
is
continuous on the set of all reals.
Integral (9) is called convergent if the limit in (9) exists and divergent otherwise. The same is concerned to the integral (10).
Def. 5. Principle value of the improper integral (10) is called the next limit
.
( 11 )
If an integral (10) converges then its principal value also converges. But there are cases when the integral (10) diverges but its principal value converges.
Ex. 2. Improper integrals
( 12 )
are
convergent for
and divergent for
.
■Let’s consider the first integral.
a) If
we can suppose
where
,
and so
,
that is the integral converges for .
b) Let
In this case
.
The integral diverges.
c) If
we put
where
,
and
.
The integral diverges.■
Ex. 3. Prove that the integral
diverges but its principal value converges.
■On the base of the formula (10)
Both limits doesn’t exist and therefore the integral diverges. On the other hand the principal value of the integral converges to zero (or equals zero), because of by the formula (11)
.■
Ex.
4. Find the area of an infinite figure bounded by Agnesi11
witch
and its asymptote (fig. 6).
The straight line
(the Ox-axis)
is a horizontal
Fig. 6 asymptote
of Agnesi witch because of
.
The figure is symmetric with respect to the -axis, and therefore its area equals
.
Note 1 (Newton-Leibniz formula for improper integrals).
Let a function be a primitive of a function . Denoting
we can represent evaluation of the improper integral (8) in the form of Newton-Leibniz formula, namely
(
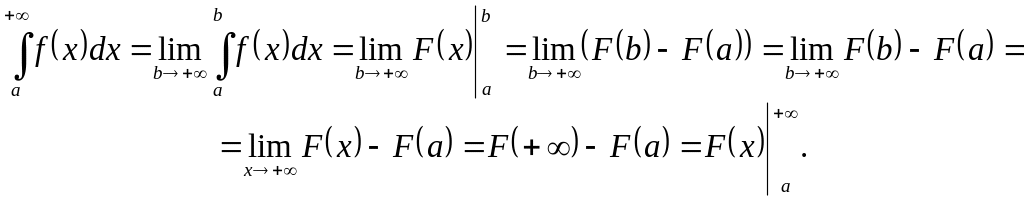
13 )
The same Newton-Leibniz formula can be written for the other improper integrals of the first kind.
Ex. 5.
.
Ex. 6. Calculate the next improper integral
.
.