Properties of primitives
1. If a function
is a primitive of a function
,
then for any constant C the
sum
is also a primitive.
2. If functions
be two primitives of a function
on a segment
,
then they differ only by a constant summand, that is their difference
is constant one on
,
const.
■By condition
and so
identically
on
.
By virtue of the corollary from Lagrange theorem (see Lecture 16,
point 2) the
difference
is constant one on
.■
Corollary. General form of a primitive of a function has the next form:
( 2 )
where is some one primitive of and C is an arbitrary constant.
Note 1. It can be said that the expression (2) represents the set of all primitives of the function .
Note 2. Geometrically, set of all primitives of a function is a family of curves depending on one parameter C.
Point 2. Indefinite integral and its properties
Def. 2. The set
of all primitives of a function
is called the indefinite integral
of this function and is denoted by a symbol
.
On the base of the definition and the Note 1
,
( 3 )
where is some primitive of the function and C is an arbitrary constant.
Ex. 3.
,
because of
.
Def. 3. Finding the indefinite integral of a function (or finding its primitive) is called integration of . To integrate a function means to find its indefinite integral (or its primitive).
Def. 4. The
symbol
is
called the integral sign;
the integrand (or the function under the
integral sign, the function to be
integrated);
the integrand (or the expression to be integrated, the expression
under the integral
sign, the element of integration, the integration element), x
the variable of integration, C
the constant of integration.
On the base of the definition of an indefinite integral and the table of the deri-vatives we can form the next
Table of simplest indefinite integrals
1.
1 a)
1 b)
1c)
2.
3.
3 a)
4.
5.
5a)
6.
6a)
7.
8.
9.
10.
11.
12.
13.
formula of high logarithm
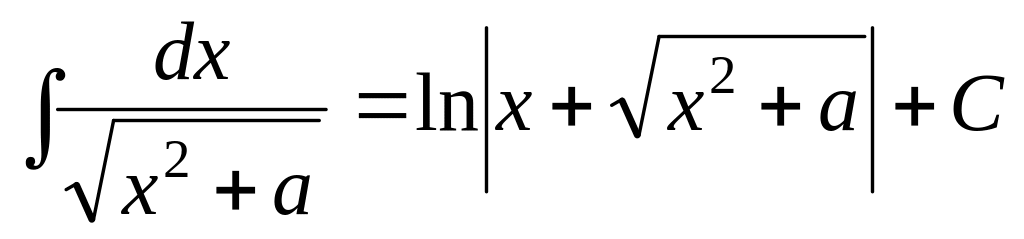formula of long logarithm
15.
16.
17.
18.
19.
20.
21.
22.
Formulas 1 – 13 are evident. The rest of them will be proved below (or directly checked by differentiation). All integrals of the table are called those tabular.
Properties of indefinite integral
1. The derivative (the differential) of an indefinite integral is equal to the function (to the expression) under the integral sign:
.
■
■
Corollary. Correctness of integration can be tested by differentiation.
2. The indefinite integral of the derivative (of the differential) of a function equals the sum of this function and an arbitrary constant:
.
Corollary. A function can be recovered from its derivative or differential with accuracy to an additive constant.
Ex. 4.
.
3 (additivity). The indefinite integral of an algebraic sum of a finite number of functions equals the sum of their integrals, for example
.
■It’s sufficient to prove that the derivatives of the left and right sides of the equality are equal. But by the property 1
■
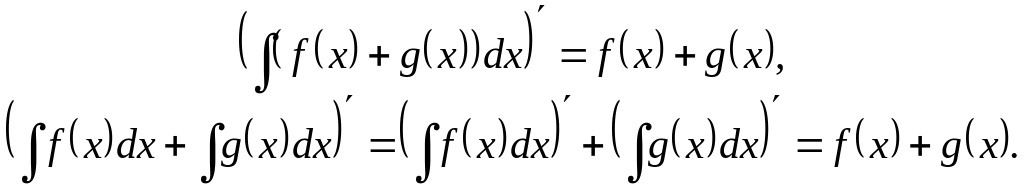4 (homogeneity). A constant factor can be taken out of the integral sign:
.
Prove the property yourselves.
Corollary 1 (linearity).
For any functions
and constants
.
Corollary 2. On the base of the linear property and the table of simplest integrals one often can fulfil so-called direct integration.
Ex. 5.
.
Ex. 6.
.
Ex. 7.
.
Ex. 8. On the base of Ex. 5-7
.