Point 3. Integration by substitution (change of variable)
Theorem 2. Let
functions
are continuous in corresponding intervals and the function
has the continuously differentiable inverse function
.
In this case the next formula (formula
of change of variable) is true
( 4 )
The formula implies returning to preceding variable x after integration with respect to the variable t. The word “differentiation” always means finding of differentials.
■The first method. The derivatives of the left and right sides of the formula (4) are equal because of
The second method. If
is a primitive of the function
,
then the function
is the primitive of the function
on the strength of
.
Therefore by virtue of definition of the indefinite integral
■
Note 3. The formula (4) is often applied “from the right to the left”, and in this case it’s useful to write it in the next form
.
( 5 )
The
formula (5) means: if an integrand is represented as a product of
some function f of
a function
and the derivative
of this latter then it’s well to put
.
Note 4. We can use any letter instead t in the formula (5).
Ex. 9.
.
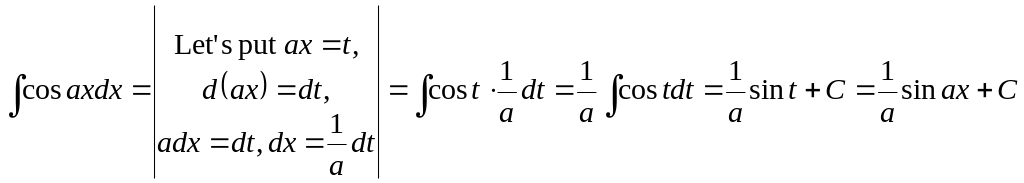Ex. 10. Prove yourselves that
.
Ex. 11.
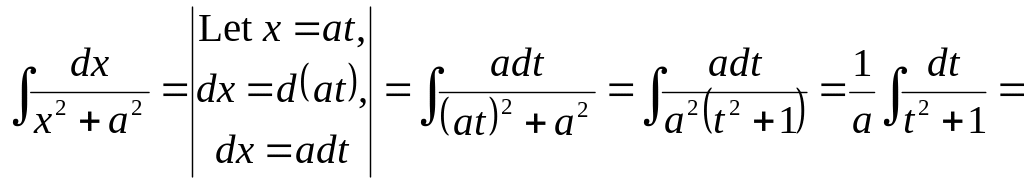
Ex. 12. Evaluate the indefinite integral
.
The integrand
is a product of a function of
,
namely
,
and the derivative of
(up to a constant factor
,
for
).
On the base of the formula (5) we can put
or better
.
We suppose that
and so
.
Therefore
.
Ex. 13. Calculate the indefinite integral
.
The integrand
is a product of the function of
and (up to a factor -20) the derivative of
.
So, putting
,
we reduce the given integral to a tabular one (see the tabular
formula (12) where we must take
)
Ex. 14. The case when an integrand is a fraction, the numerator of which is the derivative of the denominator. The integral is reduced to a tabular one (see 2)
( 6 )
For ex. a)
( 7 )
b)
( 8 )
Ex. 15. Prove that
( 9 )
Solution. Using the method of Ex. 12 we put
.
Hence,
.
Ex.16. Indefinite integrals
( 10 )
are reduced to sums of integrals of the types (8), (9) and those tabular with the help of the substitution
.
( 11 )
For example: a) Using the substitution (11), the formula (8) and the tabular integral No. 13, we get
b) With the help of (11), (9) and the
tabular integral No. 12 we obtain
Ex. 17. To evaluate the indefinite integral
we
put
,
whence
(with the help of the tabular integral No. 13)
Ex. 18. To prove the tabular formula No. 14 we’ll use so-called Euler’s substitution
