Point 3. Improper double integrals. Poisson formula

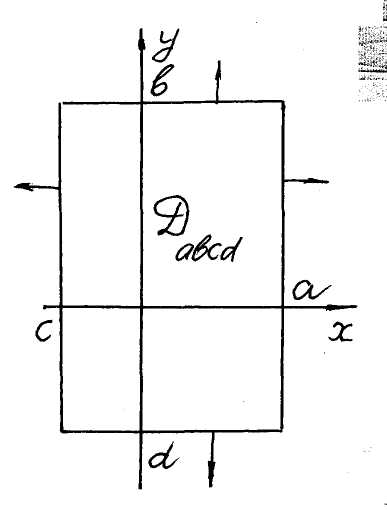
We’ll limit ourselves to improper double integrals of the first kind that is integrals of continuous functions over unbounded domains. As such the domains we’ll consider: the first quadrant

,

an infinite rectangle

and the -plane

.

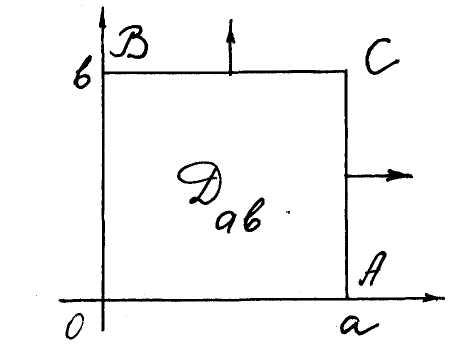
Let R is the first quadrant and is a finite rectangle with sides a and b (fig. 14). We define an improper integral Fig. 14 over R as the next limit

.

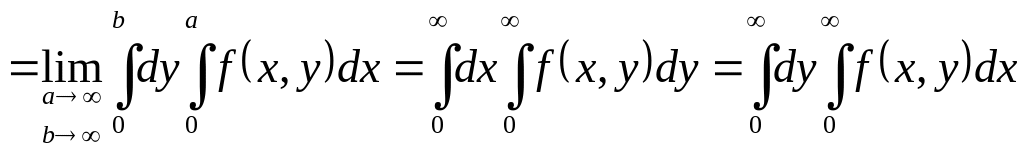As the corollary we get the formula of passing from a double integral to that repea-ting (the formula of interchange of integrations)

. ( 8 )

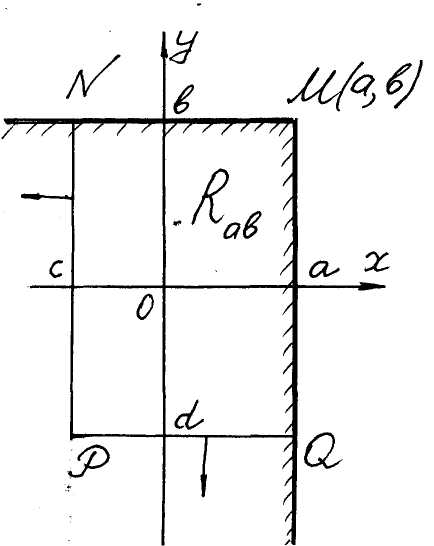
An improper integral over the rectangle (see fig. 15) we define as the limit of the integral over a finite rectangle as , and an improper integral over the -plane we define as the limit of the inte- Fig. 15 Fig. 16 gral over the same rectangle (fig. 16) as , and simultaneously . As the result we get the next two formulas

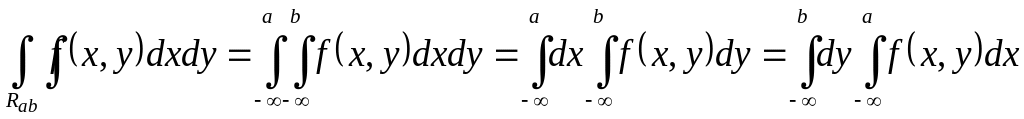, ( 9 )

. ( 10 )

Ex. 6. Poisson integrals . ( 11 )

■

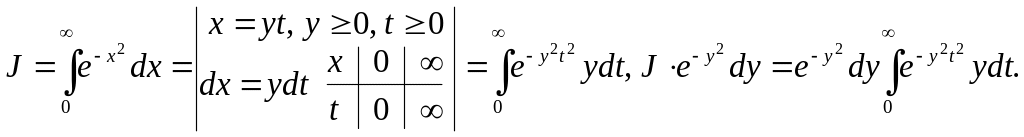
Let’s integrate with respect to y over the interval ,

.

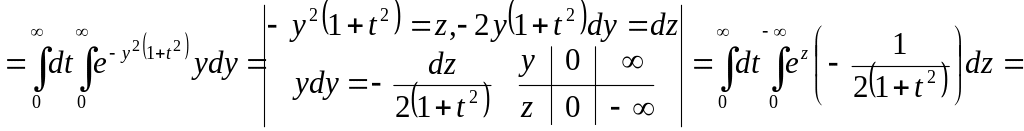
We’ve proved that , and therefore ■

Point 4. Double integral in polar coordinates

Let we study a double integral

over a domain D of the xOy-plane, and we pass to polar coordinates

, ( 12 )

coinciding the pole O with the origin and the polar axis with positive se-miaxis of the Ox-axis of Cartesian coordinate system. The domain D transforms into some domain of the -plane and the double integral passes in that over the do-main .

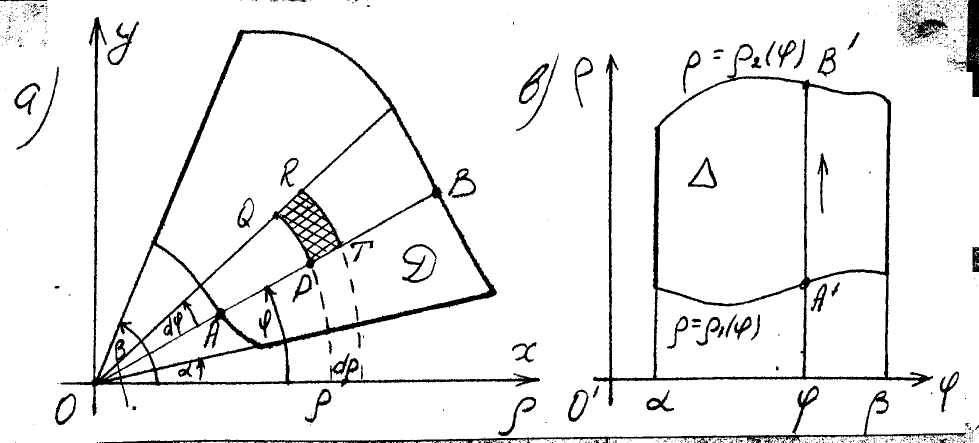To show up how the element dS of the area changes we generate an element dD of the domain D by two circles of radii centered at the origin and by two rays starting from the pole under angles to the Ox-axis (fig. 17 a). We can consider Fig. 17 dD as curvilinear rectangle PQRT with the area

.

Therefore

,

and the formula of passing to polar coordinates in a double integral can be written as

. ( 13 )

In applications we often meet the case of a domain D bounded by two rays

( 14 )

and two lines with polar equations

( 15 )

(fig. 17 a). One can describe such the domain by two double inequalities

, ( 16 )

whence it follows that a domain Δ (fig. 17 b), in which D transforms after passage to polar coordinates, is that of the first type. Therefore, by the formula (5)

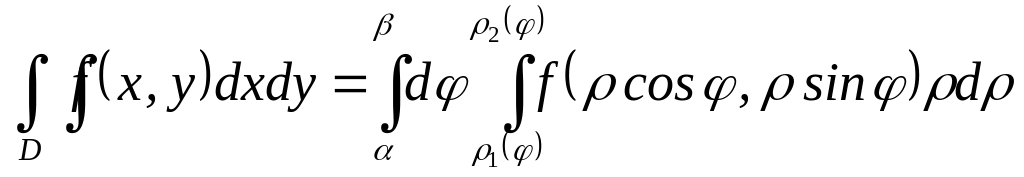. ( 17 )

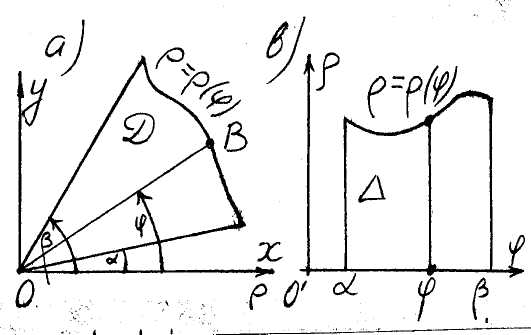If a line degenerates in the pole O we get a curvilinear sector D bounded by two rays

( 18 )

and a line with a polar equation

Fig. 18 ( 19 )

(fig. 18 a). We describe it by inequalities

, ( 20 )

whence it follows that a domain Δ (fig. 18 b) is also that of the first type. Therefore, by the formula (5)

. ( 21 )

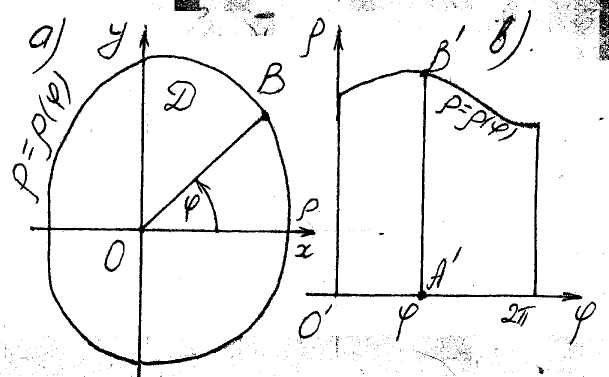Let a domain D contains the pole O, and every ray intersects the boundary of the domain in unique point (fig. 19 a). If (19) is its polar equation, then ( 22 ) Fig. 19 (fig. 19 b), and therefore

. ( 23 )

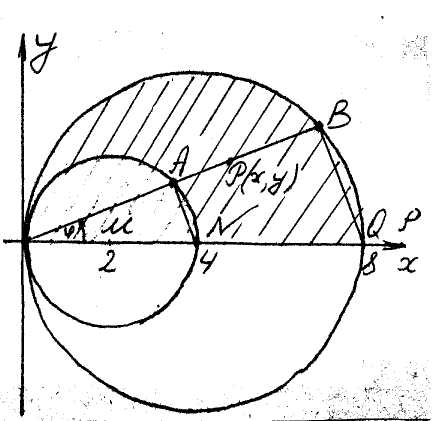Ex. 7. Evaluate the mass of a plate D containing betweem two curves

for (fig. 20), if its surface density at any point is proportional to the polar radius Fig. 20 of OP this point and equals 8 at the point .

The surface density of the plate D

and by virtue of the mechanic sense of a double integral (see (3)) we have to calculate a double integral

.

Compleating the squares we make sure that the curves are circles with radii 2 and 4 and centres correspondingly:

.

If we carry out the transition (12) to polare coordinates, we’ll get the polar equations of

and describe the domain D by two double inequalities

.

Therefore by the formula (17)

.

Ex. 8. Find the area of a figure bounded by a curve (Bernoulli lemniscate, fig. 21)

. Fig. 21 We have studied this curve in the Lecture 8, Point 2. Its polar equation is

.

Making use of the formula (2) we can write

where a domain D is the shaded area on the fig. 21. It’s evident that

.

Hence in correspondence with the formula (20) the area in question equals

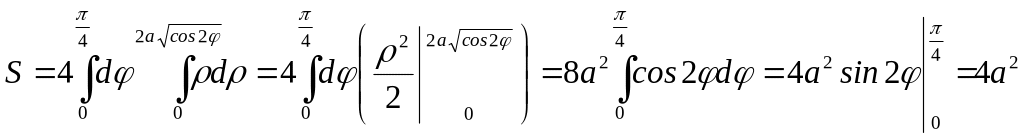
In generale case the substitution , when a domain D of the plane xOy changes in a domain of a plane , there is the next formula

.