2.8.1. Скачкообразное увеличение продаж

Для отображения скачкообразного измене­ния розничных продаж RRR, например, на 10% необходимы следующие уравнения:

RRR.KL=RRI+RCR.K, 74,R

, 103, А

где

RRR — требования (заказы), получаемые роз­ничным звеном (единицы в неделю);

RRI — исходный темп требований к рознич­ному звену, константа (единицы в не­делю);

RCR — изменение требований к розничному звену (единицы в неделю).

Согласно этим двум уравнениям, темп роз­ничных продаж до начала проигрывания имеет постоянную установившуюся величину RRI (равную 1000 единиц в неделю). После начала проигрывания величина RRR увеличивается на 100 единиц в неделю, что и дает скачкообразное увеличение розничных продаж на 10%.

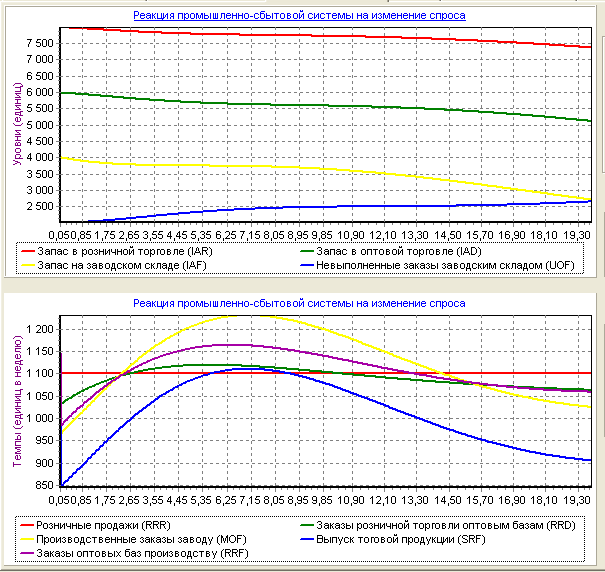
Рис. 26 - Реакция промышленно-сбытовой системы на внезапное 10-процентное увеличение розничных продаж.

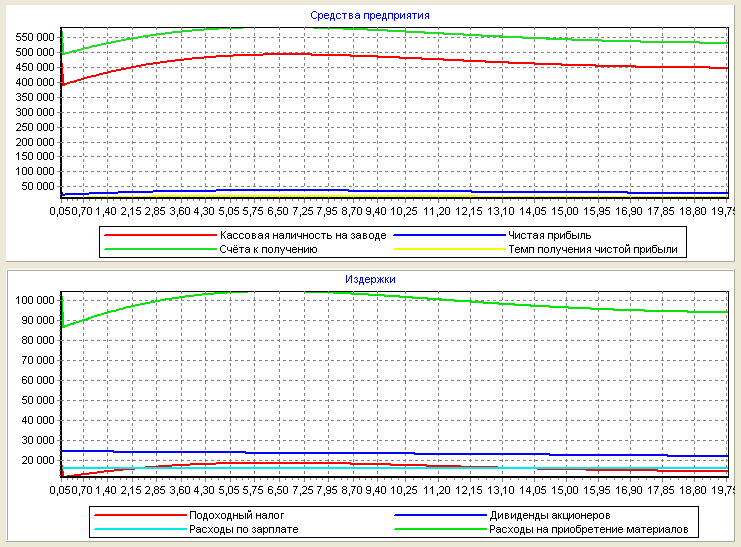
Рис. 27 - Средства и издержки предприятия при внезапном 10-процентном увеличении розничных продаж.

По рисункам 26 и 27 можно делать вывод, что при внезапном 10-процентном увеличении розничных продаж после 7 недель предприятие получило максимальную прибыль (50,000 д.е.), а потом прибыль постепенно падала в связи с уменьшением средств. Для того, чтобы прибыль предприятия увеличилась, необходимо инвестирование.

2.8.2. Годичный периодический ввод.

Рассмотрим реак­цию только на синусоидальное возмущение с периодом в один год. Оно может представлять собой непредвиденное годовое сезонное измене­ние в темпе сбыта.

Уравнения и параметры до­полним следующими уравнениями ввода:

где

RRR - требования (заказы), получаемые роз­ничным звеном (единицы в неделю);

RRI - исходный темп требований к рознич­ному звену, константа (единицы в неделю);

RCR - изменение требований к розничному звену (единицы в неделю);

TIME - календарное время, выраженное в не­делях;

SIN - функциональное обозначение синусои­дальных колебаний (в данном случае с периодом в 52 недели).

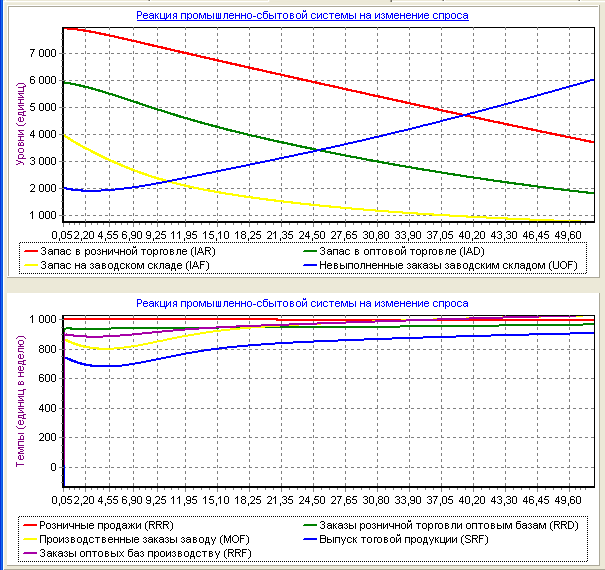
Рис. 28 - Реакция промышленно-сбытовой системы на синусоидальное возмущение с периодом в один год.

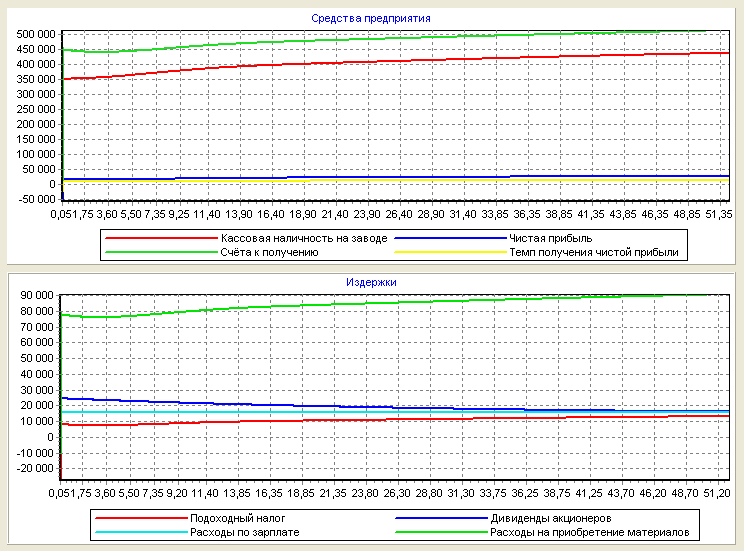
Рис. 29 - Средства и издержки предприятия при синусоидальном возмущении с периодом в один год.

По рисункам 28 и 29 можно делать вывод, что при синусоидальном возмущении с периодом в один год после 5 недель прибыль падала до минимальной (к 0 д.е.), а потом прибыль постепенно увеличилась.

2.8.3. Случайные колебания розничных про­даж.

В программе использованы 2 закона распределения случайных величин: нормальное (гауссовское) распределение и распределение Стьюдента.

Нормальное (гауссовское) распределение занимает центральное место в теории и практике вероятностно-статистических исследований. В качестве непрерывной аппроксимации к биномиальному распределению его впервые рассматривал А.Муавр в 1733 г. Через некоторое время нор­мальное распределение снова открыли и изучили К.Гаусс (1809 г.) и  П.Лаплас, которые пришли к нормальной функции в связи с ра­ботой по теории ошибок наблюдений. Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равна:

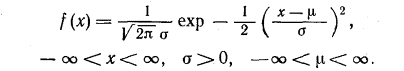
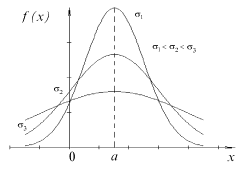
Рис. 30 – График функции нормального распределения

где  совпадает с математическим ожиданием величины Х: =М(Х), параметр s совпадает со средним квадратическим отклонением величины Х: s =s(Х). График функции нормального распределения, как видно из рисунка 30, имеет вид куполо­образной кривой, называемой Гауссовой, точка максимума имеет координаты (а; ). Значит, эта ордината убывает с возрастанием значения s (кривая «сжимается» к оси Ох) и возрастает с убыванием значения s (кривая «растягивается» в положительном направлении оси Оу). Изменение значений параметра  (при неизменном значении s) не влияет на форму кривой, а лишь перемещает кривую вдоль оси Ох.

Распределение Стьюдента получило свое название от псевдонима Student, которым английский ученый Госсет подписывал свои работы по статистике. Пусть -- независимые стандартные нормальные случайные величины. Распределением Стьюдента с степенями свободы называется распределение следующей случайной величины:

Если вспомнить введенную формулой случайную величину  , то можно сказать, что отношение имеет распределение Стьюдента. Плотность этого распределения представляет собой симметричную функцию, задаваемую формулой

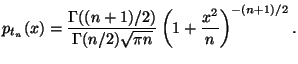
По форме график функции напоминает график плотности стандартного нормального закона, но с более медленным убыванием ``хвостов''. При последовательность функций сходится к функции , которая есть плотность распределения  . Чтобы понять, почему этот факт имеет место, следует обратить внимание на то, что по закону больших чисел знаменатель выражения  при стремится к  .

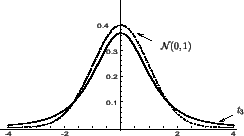
Рис. 31 - График функции распределения Стьюдента 

На рисунке 31 представлена плотность распределения Стьюдента  и плотность стандартного нормального закона.

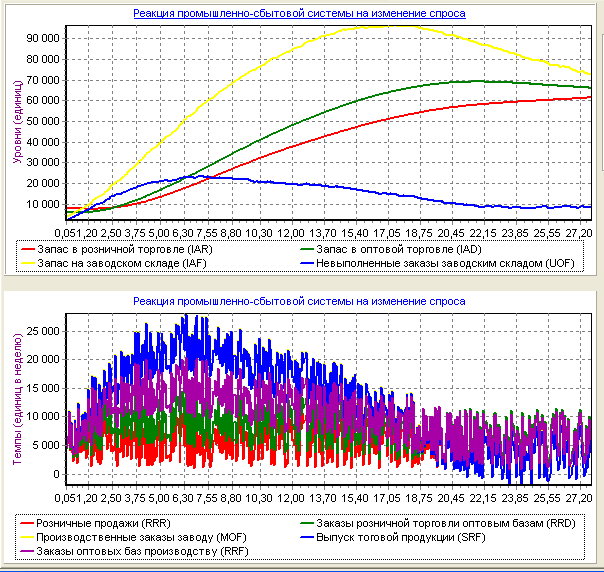
Рис. 32 -Реакция промышленно-сбытовой системы на случайные колебания розничных про­даж.

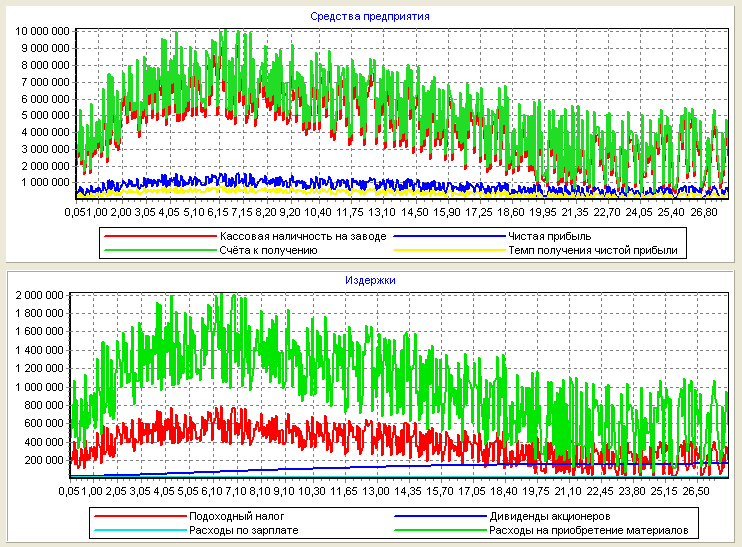
Рис. 33 - Средства и издержки предприятия при случайных колебаниях розничных про­даж.

По рисункам 32 и 33 можно делать вывод, что при случайных колебаниях розничных про­даж после 6 недель предприятие получило максимальную прибыль (1,800,000 д.е.), а потом прибыль постепенно падала до 800,000 д.е. (после 24 недель) и стремится к устойчивости. Для того, чтобы прибыль предприятия постоянно увеличилась, необходимо инвестирование.