2.1.2.Растровая развёртка окружности

Существует несколько очень простых, но не эффективных способов преоб­разования окружностей в растровую форму. Например, рассмотрим для про­стоты окружность с центром в начале координат. Ее уравнение записыва­ется как x² + y² = R². Решая это урав­нение относительно y, получим

y = ±

Чтобы изобразить четвертую часть окружности будем изменять x с еди­ничным шагом от 0 до R и на каждом шаге вычислять y. Вторым простым методом растровой развертки окружности является использование вычисле­ний x и y по формулам x = R cos α, y = R sin α, при пошаговом изменении угла α от 0⁰ до 90⁰.

Для упрощения алгоритма растровой развёртки стандартной окружности можно вос­пользоваться её симметрией относительно координатных осей и прямых y = ± x в случае, когда центр окружности не совпадает с началом ко­ординат, эти прямые необходимо сдвинуть параллельно так, чтобы они прошли через центр окружности. Тем са­мым дос­таточно построить растро­вое представление для 1/8 части окружности, а все оставшиеся точки полу­чить симметрией (рис. 2.5).

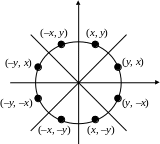
Рис. 2.14 Восьмисторонняя симметрия

Рассмотрим участок окружности из второго октанта x Є [0, R/ ]. Далее опишем алго­ритм Брезенхейма для этого участка окружности.

На каждом шаге алгоритм выбирает точку P_i (x_i, y_i), которая является бли­жайшей к ис­тинной окружности. Идея алгоритма заключается в выборе ближайшей точки при по­мощи управляющих переменных, значения которых можно вычислить в пошаговом ре­жиме с использованием небольшого числа сложений, вычитаний и сдвигов.

Рассмотрим небольшой участок сетки пикселов, а также возможные спо­собы (от A до E) прохождения истинной окружности через сетку (Рис. 2.6).

Предположим, что точка P_i-1 была выбрана как ближайшая к окружности при x = x_i-1. Теперь найдем, какая из точек S_i или T_i расположена ближе к ок­ружности при x = x_i-1 + 1.

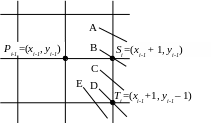
Рис. 2.15 Варианты прохождения окружности через рас­тровую сетку

Заметим, что ошибка при выборе точки P_i (x_i, y_i) была равна

D(P_i) = (x_i²+ y_i²) – R².

Запишем выражение для ошибок, получаемых при выборе точки S_i или T_i.

D(S_i) = [(x_i-1+ 1)² + (y_i-1)²] – R²

D(T_i) = [(x_i-1+ 1)² + (y_i-1 – 1)²] – R²

Если | D(S_i) | ≥ | D(T_i) |, то T_i ближе к реальной окружности, иначе выбира­ется S_i.

Введем d_i = | D(S_i) | – | D(T_i) |

T_i будет выбираться при d_i ≥ 0, в противном случае будет устанавливаться S_i.

Опуская алгебраические преобразования, запишем d_i и d_i+1 для разных ва­риантов вы­бора точки S_i или T_i.

D₁ = 3 – 2 R

Если выбирается S_i (когда d_i < 0), то d_i+1 = d_i + 4 x_i-1 + 6

Если выбирается T_i (когда d_i ≥ 0), то d_i+1 = d_i + 4 (x_i-1 – y_i-1) + 10

Существует модификация алгоритма Брезенхейма для эллипса.

static int xCenter;

static int yCenter;

static void circlePoints (int x, int y, int color )

{

putpixel ( xCenter + x, yCenter + y, color);

putpixel ( xCenter + y, yCenter + x, color);

putpixel ( xCenter + y, yCenter - x, color);

putpixel ( xCenter + x, yCenter - y, color);

putpixel ( xCenter - x, yCenter - y, color);

putpixel ( xCenter - y, yCenter - x, color);

putpixel ( xCenter - y, yCenter + x, color);

putpixel ( xCenter - x, yCenter + y, color);

}

void circle2 (int xc, int yc, int r,int color )

{

int x=0;

int y=r;

int d=1-r;

int delta1=3;

int delta2 = -2*r + 5;

xCenter=xc;

yCenter=yc;

circlePoints(x,y,color);

while (y>x)

{

if(d<0)

{

d+=delta1;

delta1 += 2;

delta2 += 2;

x++;

}

else

{

d+=delta2;

delta1 += 2;

delta2 += 4;

x++;

y--;

}

//delta2 = -2*r + 5;

circlePoints ( x, y, color );

}

}