16. Різні види рівняння кривої у просторі. Тригранник Френе.
Відображ. фігури F у фігуру F’ наз. неперерв., якщо воно близькі точки фігури F перевод. у близькі точки фігури F’.
Відображ. f фігури F у фігуру F’ наз. топологічним(гомеоморфним), якщо воно бієктивне і взаємно неперервне.
Відображ. фігури наз. локально-топологічним, якщо воно є гомеоморфним в околі кожної її точки.
Множина γ точок простору наз. елементарною кривою, якщо ця множина є образом відкритого відрізка прямої при його топологіч. відображ. в просторі.
Простою кривою наз. фігура, кожна точка якої має такий просторовий окіл, що частина фігури, яка міст. в цьому околі, є елемент. кривою.
Загальною кривою наз. фігуру, що одерж. локально топологіч. відображ. простої кривої, тобто таку криву можна покрити закінч. або зчислен. множ. елемент. кривих.
Нехай у
прямокут. репері
-
елемент. крива, яка є тополог. образом
відрізка АВ.
Якщо
на прямій АВ
як числовій осі ввести координату t,
то відображ. відрізка АВ
в
криву γ можна задати р-нями:
(1),
де x(t),
y(t),
z(t)
неперер.
ф-ії
(1) – параметрич. р-ня кривої
(2)
векторне
р-ня кривої
Дві
параметриз
наз. еквівалентними, якщо існує допустима
заміна параметра t=t(u):
Якщо
лінію можна задати р-ням:
явне
(канонічне) задання кривої.
У цьому випад. лінія є перетином 2-х циліндрів.
неявне
задання кривої. Перетин
будь-яких 2-х поверхонь.
Пряму наз. регулярною класу Ck, де k≥1 (k раз диференційовано), якщо вона допускає регулярну параметриз., тобто задання її параметрич. р-нями (1)
наз.
натуральною
параметризацією,
де
В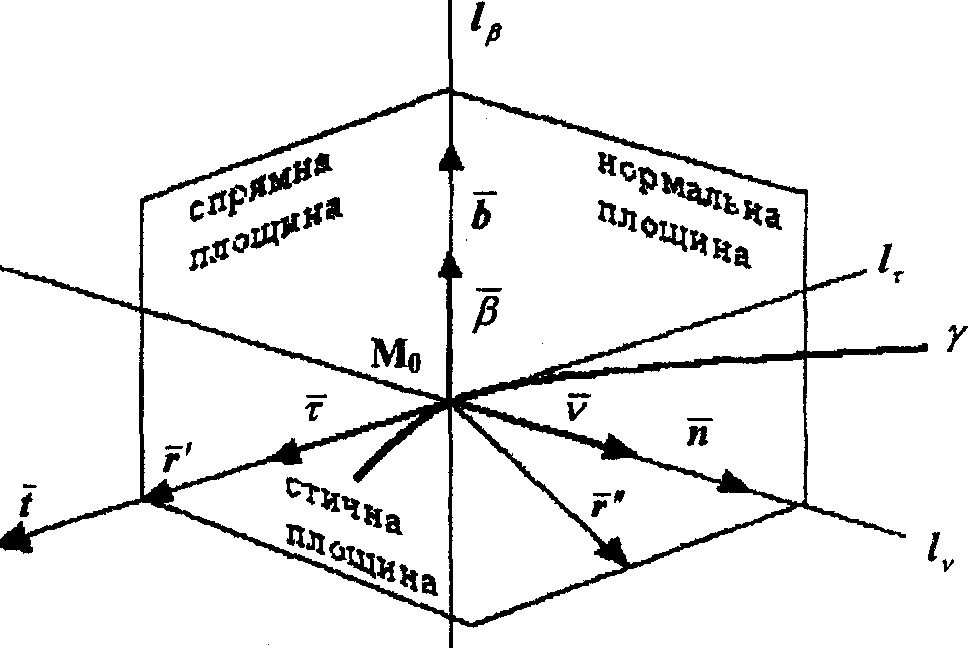
кожній точці регул. прямої класу C2
існує так званний тригранник
Френе.
lv - головна нормаль
lβ - бінормаль
lτ - дотична
На кожній з прямих тригран. вказ. одиничний вектор:
v – одинич. вектор дотичної
β - одинич. вектор головної нормалі
τ - одинич. вектор бінормалі
визнач.
стичну
площину,
lv,
що
лежить в стичній площині і перпендик.
до дотичної lτ
наз. головною
нормалю
кривої. lβ,
що проход. ч/з т.М0
і перпендик. до стичної площини наз.
бінормаллю.
lβ
і
lv
перпендик.
до дотичної визнач.
нормальну площину. Дотична
і нормаль визнач. спрямну
площину.
В кожній
точці кривої
тригранник
Френе ,
який визнач. 3-ма площинами, які попарно
перетин. по 3-м прямим, при цьому в кожній
точці кривої існує прямо кут. декартовий
базис, за базисні вектори беремо (τ,
v,
β)
Рівняння елементів тригран. Френе:
Дотична
напрямлений
вектор =
канонічне
рівняння
Бінормаль
-
напрямлений
вектор =
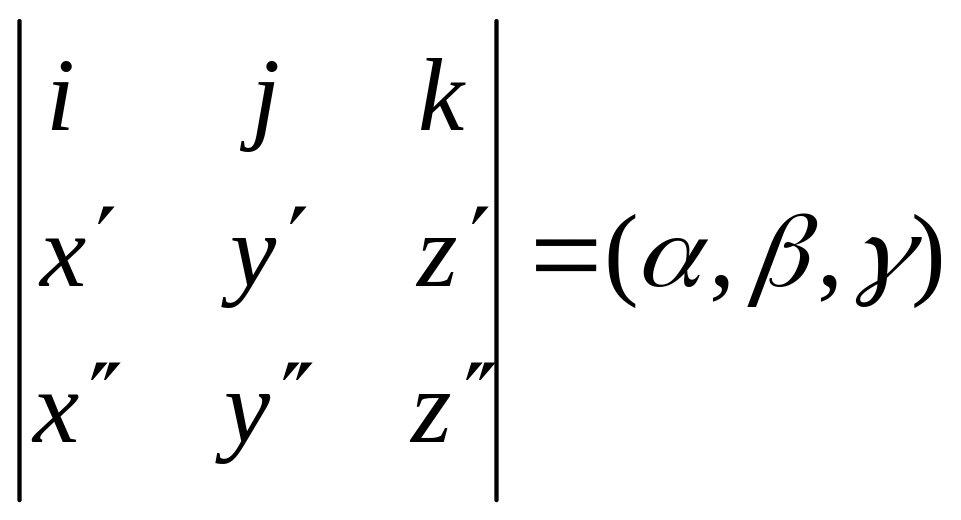
канонічне
рівняння
Головна
нормаль
-
напрямлений
вектор =
канонічне
рівняння
Нормальна
площина
Спрям
на площина
Стична
площина
17. Кривина та скрут просторової кривої. Формули Френе.
Якщо
крива
,
то визнач. її кривина
k
– модуль швидкості обертання дотичної
по віднош. до довжини дуги:
.
Кривина
кривої
обчисл. за ф-лою
.
(1)
Якщо
крива задана параметрич. р-нями
то
(2)
Зокрема,
якщо в ролі параметра кривої вибраний
натур. параметр s,
то
,
а в корд.
.
(3)
Точки в яких k = 0, наз. точками розпрямлення. Ця назва виправдана такою властив.: для того, щоб крива γ була прямою лінією, необх. і досить, щоб у кожній її точці k = 0.
Величина
наз.
радіусом
кривини кривої.
Якщо від т.М
кривої на голов. нормалі в додат. напрямку
відклас. відрізок довжиною R,
тот одержана т.C
носить назву центра кривини кривої, що
відпов. т.М.
Якщо
крива,
,
то скрут
χ
цієї кривої (без урахування знаку) – це
швидкість обертання стичної площини
навколо дотичної або, що те саме, швид.
зміни напряму бінормалі:
.
Скрут
кривої, заданої р-ням
визнач.
ф-лою
(4)
або в корд. вигляді
(5)
У випад.
натур. параметриз. кривої, тобто
,
то
(6)
або
(7)
Рівність нулю скрута кривої у всіх точках є необх. і достат. умовою того, щоб крива була плоскою.
Точки, в яких χ = 0, наз. точками сплощення кривої.
Як виплив. із ф-ул для визнач χ,в точках розпрямлен. кривої (тобто в точках, де k = 0) скрут невизначю
ТеорФрене: похідні від базисних векторів в локальній системі координат є лінійними комбінаціями цих базисних векторів.
,
,
- формули Френе
Вивід формул Френе:
1)
;
-
залежать від
.
2)
3).