11. Перетворення подібності. Гомотетія. Аналітичне задання подібності. Група подібності та її властивості.

Перетворення площини наз. перетворенням подібності (подібністю), якщо існує число таке, що для будь-яких точок А і В і їх образів і виконується умова .

Якщо , то отримаємо рух площини.

Тобто рух – це частковий випадок перетворення подібності.

Розг. приклад перетворення подібності, відмінного від руху.

Зафіксуємо точку і число _µ .

Кожній точці М площини поставимо у відповідність точку таку, щоб виконувалась рівність: (2) (рис.5).

Т аке перетвор. площини наз. гомотетією з центром в т. і коефіцієнтом m.

Покажемо, що гомотетія є перетвор.подібності.

Розг. ще одну т.N площ. та її образ – т. (рис.5). Тоді .

Отже,

(3)

Таким чином гомотетія є перетвор.подібності з коефіцієнтом k= .

• якщо , то маємо тотожне перетворення,

• якщо 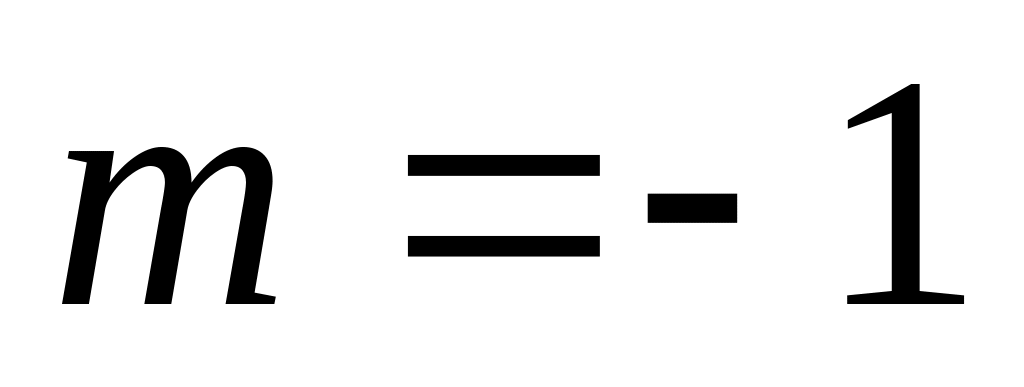, то це перетворення – центральна симетрія відносно т. ,

• якщо , то гомотетія відмінна від руху.

З адамо на площині с-му коор. , і розг. т.М та її образ т. п ри гомотетії з центром в т.О(0,0) (рис.6). Одерж. аналітич. задання такої гомотетії.

Нехай точка М має координати x, y, а точка має координати Тоді за означенням гомотетії . Перейшовши до координат, отримаємо:

(4)

Розглянемо властивості гомотетії.

1. Гомотетія з коефіцієнтом переводить пряму, яка не проходить ч/з центр гомотетії в || їй пряму, а пряму яка проход. ч/з центр гомотетії –в себе.

Доведення. Нехай пряма l в деякій с-мі коор. має р-ня: . Для знаходж. р-ня її образа викорис. ф-ли (4). З них отрим.: і підставивши в р-ня прямої l одержимо рівняння . Отже,  – пряма || до прямої l, якщо С≠0, тобто якщо пряма не проходить ч/з поч.. с-ми коор. і , якщо С=0 (пряма l проходить ч/з поч.. координат).

2. Гомотетія зберігає просте відношення трьох точок.

Доведення. Нехай при гомотетії точки .

Розг. їх прості відношення і , або

.

Але, згідно рівності (3) . Отже,

, або Таким чином

3. Гомотетія перевод. відріз. у відріз., промінь у пром., півплощ. в півплощ.

Доведення випливає з перших двох властивостей.

4. Гомотетія переводить кут у рівний йому кут.

Доведення.

Нехай АВС даний кут, а А'В'С' – його образ. За формулою (3) отримаємо: .

5. Гомотетія зберігає орієнтацію площини.

Доведення. Розглянемо репер R=(B,A,C) і його образ при гомотетії = Так як , а , то R і однаково орієнтовані, тобто гомотетія зберігає орієнтацію площини.

Отже, гомотетія має такі ж властивості як і рухи першого роду.

Покаж., що послідовне викон. двох перетворень подібності (їх композиція) є перетвор. подібності. Розгул. два перетвор. подібності f з коефіц. подібності k₁ і g з коефіц. k₂ та довільні дві точки А і В площини. Тоді :

 . За означ. подібності Отже , .

Таким чином композиція двох перетворень подібності з коефіц. k₁ і k₂ буде перетвор. подібності з коефіц.

Теор3. Якщо f – перетвор. подібності з коефіц. k, а h – гомотетія з цим же коефіц. k і з центром в т. , то існує єдиний рух , такий що . (5)

Доведення. Покаж., що такий рух існує. Розг. перетворення (6) Тоді g – це перетвор. подібності з коефіц. , тобто є рухом. Помнож. обидві частини рівності (6) на h справа :

. Отже, і існування руху g доведено.

Покажемо, що такий рух єдиний.

Припус., що існує ще один рух , такий, що . Помнож. обидві частини цієї рівності на : або

Отже, ми довели, що перетворення подібності – це композиція гомотетії і руху.

Так як гомотет. має такі ж влас. як і рух, то з урах. теор. і подібність має влас.:

1. Подібність переводить пряму в пряму, паралельні прямі в || прямі.

2. Подібність зберігає просте відношення трьох точок.

3. При перетворенні подібності кут переходить в рівний йому кут.

4. При подібності півплощина переходить у півплощину.

5. Подібність змін. орієнтацію площини, якщо рух змін. орієнтацію площини (рух невласний) і не змін. в противному (якщо рух власний). В першому випад. перетвор.подібності наз. невласним (перетвор. подібності 2-го роду ), в другому – власним (перетвор. подібності 1-го роду ).

Нехай перетвор. подібності з коефіц. k. Задамо на площині деяку с-му коор. і отрим. в ній аналіт. задання подібності .

Скор. теор3. Розг. гомотетію h з центром в т.О і коеф. k. Її аналіт. задання

Нехай g – рух, який задовол. рівність (5). Аналіт. задання руху

Якщо т.М(x,y) при перетвор. подібності перейде в т. , то аналіт. задання подібності матиме вигляд: (7)

Теоре4. Будь-яке перетвор. подіб., відмін. від руху, має тільки 1 нерухому точ.

Доведення. Нехай перетвор. подібності має аналіт. задання (7). Т.М(х,у) буде нерухом. точкою цього перетвор. ↔, коли

Розг. визначник C цієї с-ми :

Якщо ε=1, то а якщо ε= -1, то C=1–k². Отже, при Таким чином с-ма має єдиний розв’яз. – єдину нерух. точ. перетвор.

Наслід. Перетвор. подібності, яке не має нерухом. точок, або має більше ніж одну нерух. точку є рухом.

Класифікацію перетвор. подібності Власні перетворення подібності.

Нехай перетвор. подібності з коеф. k має тільки 1 нерух. точку, познач. її О. Познач. h - гомотетію з центром О і коеф. k. За теор3 існує такий рух g, що . Оскільки і h власні перетвор. подібності то і рух g – власний причому . Таким чином – поворот навколо т.О. Можливі 3 випадки :

1. g – тотож. перетвор. В цьому випад. f=h, отже, f- гомотетія з додат. коеф.

2. g – центральна симетрія. Тоді - гомотетія з від’єм. коеф. .

3. g – поворот на кут , і . В цьому випад. f- композиц. гомотетії і повороту. Вона наз. центрально-подібним поворотом.

Отже, власне перетвор. подібності, відмінне від руху гомотетія, або центрально-подібний поворот.

Невласні перетворення подібності.

Згідно теор4 перетвор. подібності f з коеф.k має єдину нерух. т.О ( ). За теор.3 , де g – невлас. рух. Так як О – нерух. точка руху g, то g – осьова симетрія. У цьому випад. f – композиц. гомотетії і осьової симетрії і наз. центрально-подібною симетрією.

Отже, існує три типи перетворення подібності, відмінного від руху:

1. Гомотетія.

2. Центрально-подібний переворот.

3. Центрально-подібна симетрія.

Познач. Р – множину всіх перетворень подібності. Покажемо, що Р – група. Потрібно перевірити 2 умови: замкненість і існув. обернен. елемента. Композит. двох перетвор. подібності буде подібністю (коеф. подібності ).

Очевидно, що для будь-якого перетворення подібності f з коефіцієнтом k існує обернене з коеф. . Отже, множина Р всіх перетвор. подібності утвор. групу. Операція тут – послідовне викон. двох перетворень подібності (їх композиція).

Наз. вона групою подібностей.

Так як будь-який рух є частков. випад. перетвор. подібності ( подібність з коеф. k=1), то група рухів є підгрупою групи подібнос. Ясно що всі підгрупи групи рух і будуть в свою чергу підгрупами і групи подібностей.