
- •3.Разложение сил на две составляющие.
- •4. Связи и реакции связей. Принцип освобождения.
- •5. Распределённые нагрузки
- •6. Геометрический способ определения равнодействующей плоской системы
- •7. Геометрическое условие равновесия плоской системы сходящихся сил.
- •8. Проекции силы на оси координат.
- •10. Момент силы относительно точки
- •11. Пара сил и момент пары. Условие равновесия плоской системы пар.
- •12. Опоры и опорные реакции балок.
- •13. Лемма о параллельном переносе силы.
- •14. Приведение плоской системы произвольно расположенных сил к данному центру.
- •15. Момент силы относительно оси.
- •1) Момент силы относительно оси равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси;
- •2) Момент силы относительно оси равен нулю, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы.
- •16. Основные понятия сопротивления материалов.
- •17. Основные гипотезы и допущения
- •18. Виды нагрузок и основных деформаций.
- •19. Закон Гука при растяжении и сжатии.
- •21. Кручение. Понятие о кручении круглого цилиндра.
- •22. Эпюры крутящих моментов.
- •23. Напряжения и деформации при кручении.
- •24. Расчетные формулы на прочность и жесткость при кручении.
- •25. Изгиб. Понятие о чистом изгибе прямого бруса.
- •26. Изгибающий момент и поперечная сила.
- •27. Дифференциальные зависимости при изгибе.
- •. Выводы:
- •29. Нормальные напряжения при чистом изгибе.
- •30.Расчетная формула на прочность при изгибе.
13. Лемма о параллельном переносе силы.

Докажем лемму: Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Пусть в точке А твердого тела приложена сила F (рис. 4.1). Приложим теперь в точке В тела систему двух сил F' и F²-, эквивалентную нулю, причем выбираем F'=F (следовательно, F"=–F). Тогда сила F~(F, F', F"), так как (F',F")~0. Но, с другой стороны, система сил (F, F', F") эквивалентна силе F' и паре сил (F, F"); следовательно, сила F эквивалентна силе F' и паре сил (F, F"). Момент пары (F, F") равен M=M(F,F")=BAxF, т.е. равен моменту силы F относительно точки В M=MB(F). Таким образом, лемма о параллельном переносе силы доказана.
14. Приведение плоской системы произвольно расположенных сил к данному центру.
Пусть
на тело действует система произвольно
направленных, лежащих в одной плоскости
сил ![]() .
.
Выберем в плоскости произвольную точку О, которую назовем центром приведения и перенесем в эту точку все силы (рис. 29, а
В результате получим новую систему сил:
![]()
с моментами присоединенных пар:
![]()
Систему
сил перенесенную в точку О заменим одной
силой ![]() приложенной
в той же точке О:
приложенной
в той же точке О:
![]()
Сложение пар дает одну пару с моментом:
![]()
Вектор
,
равный геометрической сумме всех сил
называют главным
вектором системы.
Величину ![]() ,
равную сумме всех моментов относительно
центра О, называют главным
моментом системы
относительно центра О.
,
равную сумме всех моментов относительно
центра О, называют главным
моментом системы
относительно центра О.
Итак: Всякая плоская система сил, действующая на твердое тело при приведении к произвольно взятому центру О заменяется одной силой , равной главному вектору системы и приложенной в Центре приведения О, и одной парой с моментом , равным главному моменту системы сил относительно центра О.
Для задания плоской системы сил достаточно задать ее главный вектор и главный момент относительно некоторого центра О. Главный вектор не зависит от положения центра приведения O (рис. 29, б).
Главный момент зависит от положения центра приведения О и его всегда нужно указывать.
При приведении произвольно расположенных сил на плоскости к данному центру возникают стандартные случаи, называемые приведением системы к простейшему виду. Рассмотрим эти случаи, имея в виду, что определено согласно (4.2.3), а согласно (4.2.4):
![]()
Все силы, приложенные к твердому телу, уравновешиваются.
![]()
Все силы приводятся к одной паре сил.
![]()
Все силы приводятся к равнодействующей.
![]()
Заданная система сил так же приводится к равнодействующей.
В данной главе мы не приводим теорему Вариньона о моменте равнодействующей плоской системы, считая, что параграф 7 главы 2 дает представление как о самой теореме, так и о ее доказательстве.
15. Момент силы относительно оси.
Для характеристики вращательного действия силы на тело, закрепленное на оси, служит момент силы относительно оси – алгебраический момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с этой плоскостью (рисунок 1.3).
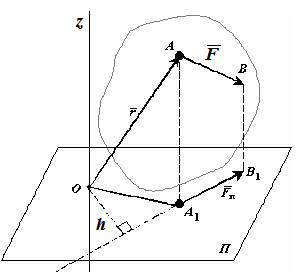
Рисунок 1.3
Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную к оси, стремится вращать тело вокруг положительного направления оси против движения часовой стрелки, и отрицательным, если она стремится вращать тело по движению часовой стрелки:
Mz(F) = Mo(FП) = ±hFП,
где FП – вектор проекции силы F на плоскость П, перпендикулярную к оси Oz, точка O – точка пересечения оси Oz с плоскостью П.
Свойства момента силы относительно оси:
