Обчислення рангу матриці

Основними методами обчислення рангу матриці є методи оточення мінорів (теоретичний) і метод елементарних перетворень (практичний).

Метод оточення мінорів полягає в тому, що в ненульовій матриці шукається довільний базисний мінор.

Метод елементарних перетворень полягає в тому, що за допомогою елементарних перетворень знаходиться деяка максимальна лінійно незалежна система рядків матриці. Можливо із зведенням матриці до трикутного вигляду (метод Гауса).

Властивості

• Тільки нульова матриця має нульвий ранг.

• 

• 

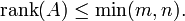
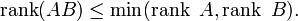
5. Система лінійних алгебраїчних рівнянь (СЛАР) — в лінійній алгебрі це система лінійних рівнянь виду:

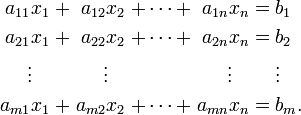
Це система m лінійних рівнянь з n невідомими, де

є невідомими,

є коефіцієнтами системи,

- вільними членами^[1].

Системи лінійних алгебраїчних рівнянь відіграють важливу роль у математиці, оскільки до них зводиться велика кількість задач лінійної алгебри, теорії диференціальних рівнянь, математичної фізики, тощо, та областей фізики й техніки, де застосовуються ці математичні теорії.

Векторна форма еквівалентна матричній формі запису

де A — матриця m×n, x — вектор з n компонент, b — вектор з m компонент.

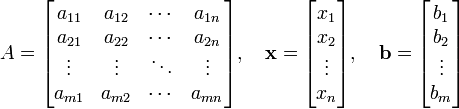
Число векторів в базисі лінійної оболонки векторів є рангом матриці.

6. §8 Обернена матриця, розв`язок матричних рівнянь

При розгляді дій з матрицями не вводиться операція ділення. Але можливо ввести поняття, яке дозволяє дати деякий еквівалент цій дії.

Визначення. Квадратна матриця В називається оберненою квадратній матриці А, якщо добуток А·В є одинична матриця.

Доведемо, що для будь-якої квадратної матриці А, визначник якої відмінний від нуля, існує одна і тільки одна обернена матриця, і приведемо спосіб її обчислення.

Нехай задана матриця

.

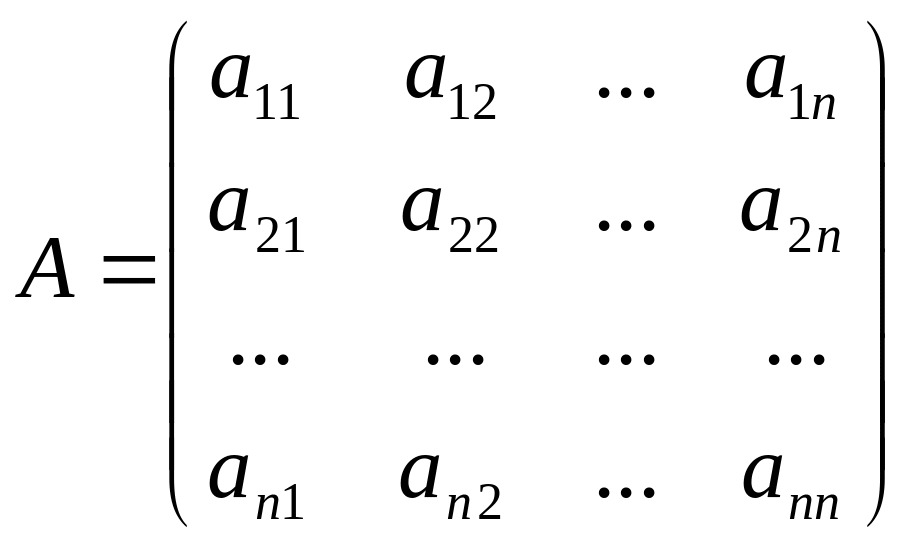
Нехай

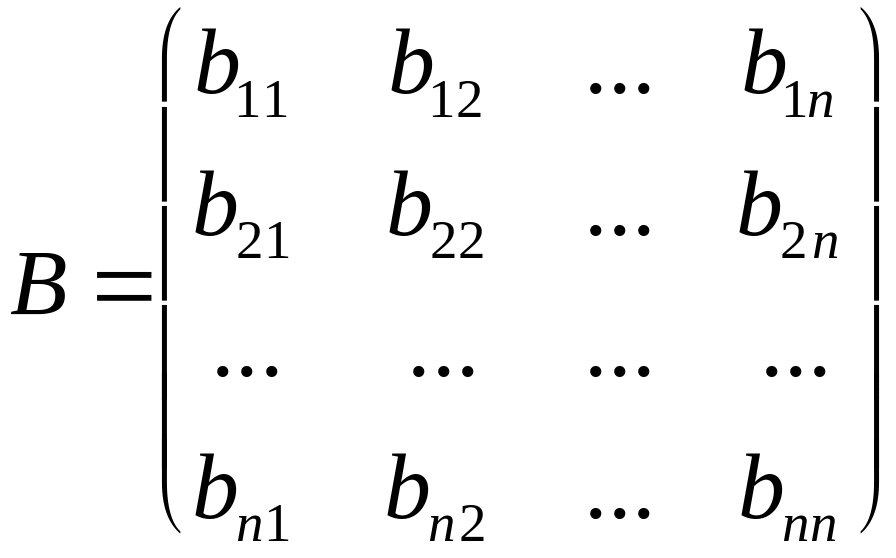
є шукана матриця і 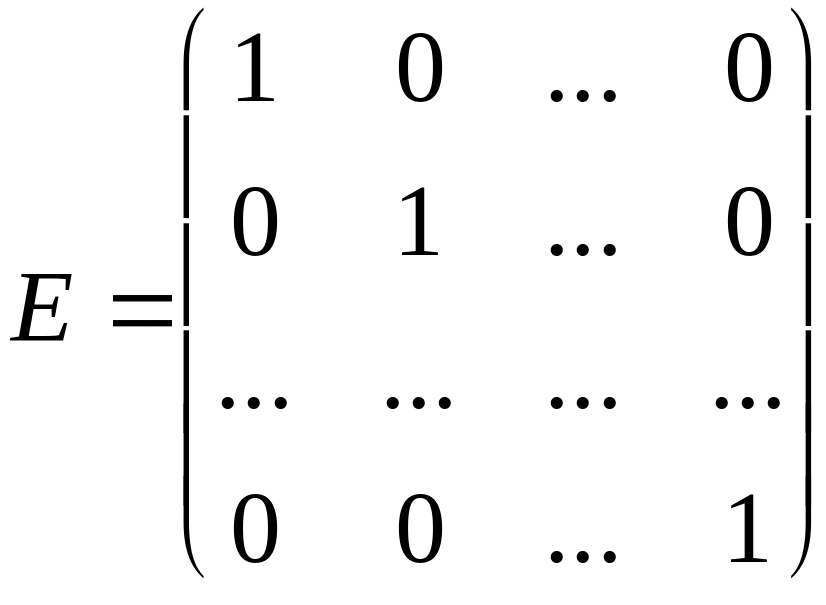- одинична матриця того ж порядку n.

Згідно умови А·В=Е, тому для визначення n² елементів b_ік матриці В ми маємо n систем рівнянь першого порядку, кожна з яких містить n рівнянь:

Такі системи мають одну і ту ж основну матрицю А.

Згідно припущення , тому кожна система має єдиний розв`язок, який можливо обчислити за формулами Крамера. Оскільки в правій частині в кожній системі тільки один елемент дорівнює одиниці, а всі інші дорівнюють нулю, тоді

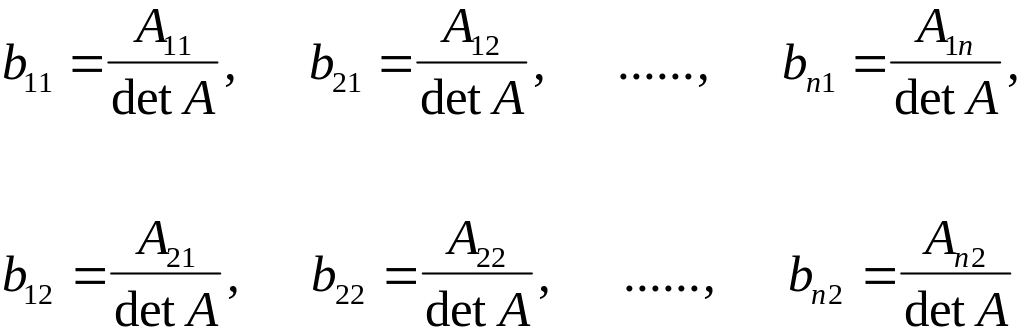
і взагалі , i,k=1,2,...,n.

Отже, матриця В, обернена матриці А, яка позначається частіше символом А^-1, має вигляд

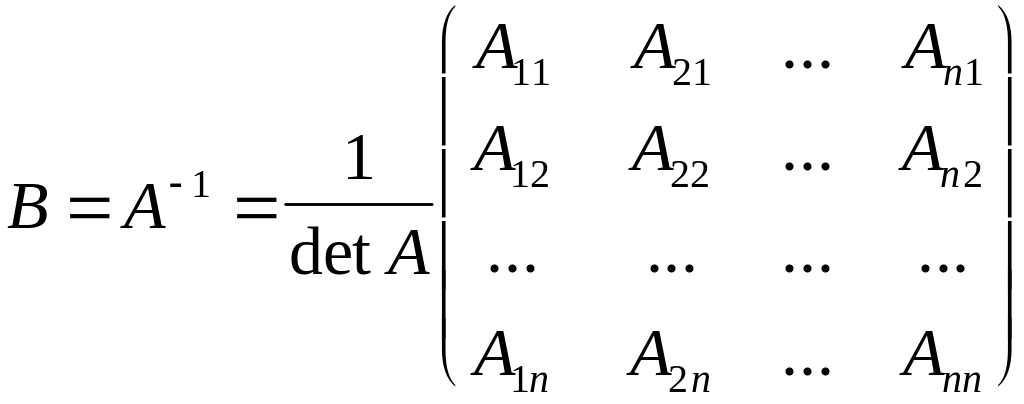(1)

Раніше було вказано, що взагалі кажучи, для довільних матриць А і В . Але можливо довести, що А^-1·А=А·А^-1.

Дійсно

Але сума добутків елементів будь-якого рядка матриці на алгебраїчне доповнення відповідних елементів другого рядка дорівнює нулю, а сума добутків елементів будь-якого рядка матриці на відповідні алгебраїчні доповнення елементів того ж рядка дорівнює самому визначнику.

Тому

і отже, А^-1·А=Е=А·А^-1

Поняття «обернена матриця» може бути використано для розв`язку матричних рівнянь.

Нехай, наприклад, задане рівняння АХ=В, де А і В - задані квадратні матриці порядку n, а Х - шукана квадратна матриця того ж порядку. Нехай . Тоді обчислюємо матрицю А^-1 і помножимо ліву і праву частини заданого рівняння зліва на А^-1:

А^-1(АХ)=А^-1В

Оскільки

А^-1(АХ)=(А^-1А)Х

(згідно асоціативної властивості множення матриць), тоді

А^-1(АХ)=ЕХ=Х

і одержуємо

Х=А^-1В

Для обчислення матриці А^-1 , оберненої матриці А, можливо, звичайно, використати формули (1). Але, як правило, значно вигідніше використати для цього метод повного виключення. Це доцільно ще і тому, що всі n систем рівнянь, які служать для визначення стовпців матриці А^-1 , відрізняються тільки правими частинами. Тому процес перетворення розширених матриць цих систем можна проводити одночасно для всіх матриць.

7. Метод Крамера (Крамера правило) — спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним). Метод було створено Габріелем Крамером у 1750 році.

Для системи лінійних рівнянь з невідомими (над довільним полем)

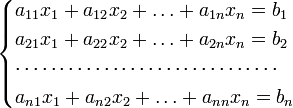
з визначником матриці системи , що не рівний нулю, розв'язок записується у такому вигляді:

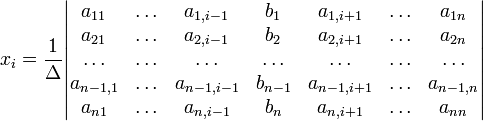
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів). Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c₁, c₂, …, c_n виконується рівність:

У такій формі формула Крамера справедлива без припущення, що не рівне нулю, не треба навіть, аби коефіцієнти системи були елементами цілісного кільця (визначник системи навіть може бути дільником нуля у кільці коефіцієнтів). Також можна вважати, що або набори та , або набір складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем. В такому вигляді формула Крамера використовується, наприклад, при доведенні формули для визначника Грама і Леми Накаями.

. Формули Крамера і матричний метод розв'язання систем лінійних рівнянь не мають серйозного практичного застосування, оскільки пов'язані з громіздкими викладками. Практично для вирішення систем лінійних рівнянь найчастіше застосовується метод Гаусса, що складається в послідовному виключенні невідомих за такою схеме.Для того щоб вирішити систему рівнянь

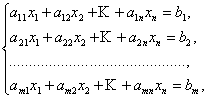  виписують розширену матрицю цієї системи 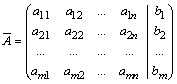і над рядками цієї матриці виробляють елементарні перетворення, приводячи її до вигляду, коли нижче головної діагоналі, що містить елементи будуть розташовуватися нулі. Дозволяється: 1) змінювати порядок рядків матриці, що відповідає зміні порядку рівнянь, 2) множити рядки на будь-які відмінні від нуля числа, що відповідає множенню відповідних рівнянь на ці числа, 3) додавати до будь рядку матриці іншу, помножену на відмінне від нуля число , що відповідає додатку до одного рівняння системи іншого, помноженого на число. За допомогою цих перетворень кожного разу виходить розширена матриця нової системи, равносильной вихідної, тобто такої системи, рішення якої збігається з рішенням вихідної системи. Розглянемо метод Гаусса на прикладах.

Пример 14. Установить совместность и решить систему

 

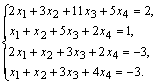
Рішення. Випишемо розширену матрицю системи і поміняємо місцями першу і другу рядка для того, щоб елемент а11 дорівнював одиниці (так зручніше проводити перетворення матриці).

.

 

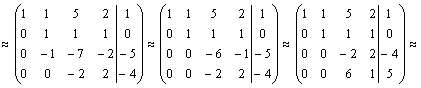
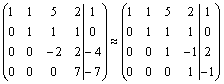Маємо  Ранги матриці системи та її розширеній матриці збіглися з числом невідомих. Згідно теоремі Кронекера-Капеллі система рівнянь сумісна і рішення її єдино. Випишемо систему рівнянь, розширену матрицю якої ми отримали в результаті: перетворень

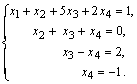
Отже, маємо  Далі, підставляючи   втретє рівняння отримуємо  Підставляючи  и  в друге рівняння отримуємо  і на кінець підставляючи в в перше рівняння  получим    Таким чином отримуємо рівняння   

8.Метод Гауса — Жордана використовується для розв'язання систем лінійних алгебраїчних рівнянь, знаходження оберненої матриці, знаходження координат вектора у заданому базисі, відшукання рангу матриці. Метод є модифікацією методу Гауса. Названий на честь Гауса та німецького математика та геодезиста Вільгельма Йордана.

Алгоритм

1. Обирається перша зліва колонка, що містить хоч одне ненульове значення.

2. Якщо верхнє число у цій колонці - нуль, то обмінюється увесь перший рядок матриці з іншим рядком матриці, де у цій колонці нема нуля.

3. Усі елементи першого рядка діляться на верхній елемент обраної колонки.

4. Від рядків, що залишились, віднімається перший рядок, помножений на перший елемент відповідного рядка, з метою отримання у якості першого елемента кожного рядка (крім першого) нуля.

5. Далі, повторюємо ці операції із матрицею, отриманою з початкової матриці після викреслювання першого рядка та першого стовпчика.

6. Після повторення операцій n-1 разів отримаємо верхню трикутну матрицю.

7. Віднімаємо від передостаннього рядка останній рядок, помножений на відповідний коефіцієнт, щоб у передостанньому рядку залишилась лише 1 на головній діагоналі.

8. Повторюємо попередній крок для наступних рядків. У результаті отримуємо одиничну матрицю і рішення на місці вільного вектора (над ним необхідно виконувати ті самі перетворення).

Якщо всі вільні члени , система лінійних алгебраїчних рівнянь називається однорідною. Однорідна система має очевидний розв'язок, у якому всі . Цей розв'язок заведено називати тривіальним. Відмінні від тривіального розв'язки існують тільки тоді, коли матриця вироджена.

Системи лінійних рівнянь

Запишемо систему рівнянь у матричному вигляді

АХ = В, (3.32)

де

Матриця А є квадратною порядку n; вектор-стовпець Х має розмір n 1; вектор-стовпець В — порядок n 1.

Якщо матриця А невироджена, тобто rgA = n і , то система лінійних рівнянь (3.32) має єдиний розв'язок виду

(3.33)

Приклад 3.5. Знайти розв'язок системи

У матричному виді:

AX = B;

отже,

.

= –2 – 15 = –17 — матриця невироджена.

Запам'ятайте: для матриці обернена матриця має вигляд .

.

Отже,

Розв'язок системи: = 1; = 3.

Розглянемо однорідну систему лінійних рівнянь:

АХ = 0 (3.34)

Нехай А — квадратна матриця n-го порядку; Х — вектор-стовпець розміру n 1.

Тривіальний розв'язок має вигляд: . Нетривіальний розв'язок може існувати лише за умови, що визначник матриці А дорівнює нулю:

Коли це так, то система матиме безліч розв'язків. Їх можна нормувати, вимагаючи, наприклад, щоб виконувалася рівність

(3.35)

Приклад 3.6. Знайти нетривіальні розв'язки однорідної системи рівнянь.

(3.36)

, це означає, що задана система має нетривіальні розв'язки.

Матрицю А можна записати як систему трьох векторів:

Систему (3.36) подамо як лінійну комбінацію вектора :

(3.37)

Неважко побачити, що ; розв'язками системи (3.36) будуть і ці самі значення, помножені на будь-які числа, які задовольняють рівняння (3.37). Отже, система векторів є лінійно залежною, причому розв'язки системи лінійних рівнянь (3.36) є коефіцієнтами лінійної комбінації вектора :

Означення 3.21. Рівняння відносно називають характеристичним рівнянням матриці А.

єКорені цього рівняння характеристичними коренями (характеристичними числами, власними значеннями) матриці А.

Візьмемо будь-який корінь характеристичного рівняння (3.41) і підставимо в систему рівнянь (3.40). Дістанемо рівняння

яке має нетривіальний розв'язок, оскільки .

Нехай цим розв'язком є вектор . Такий вектор є характеристичним, або власним, вектором матриці А, який відповідає характеристичному кореню.

Якщо матриця А має n різних характеристичних коренів, то припускатимемо, що вона має і nрізних власних векторів (задачі, які мають кратні характеристичні корені, в економіці зустрічаються рідко).

Власні вектори визначаються з точністю до множення на скаляр. Це не завжди зручно.

Отже, якщо власні вектори матриці А розміщені у вигляді стовпців матриці Х, то добуток перетворює матрицю А на діагональну матрицю, яка має характеристичні корені  на головній діагоналі.

9.

10. Моде́ль міжгалузе́вого бала́нсу Лео́нтьєва, яку також називають моделлю «витрати — випуск» є основою багатьох лінійних моделей виробничого сектора економіки. За неї Василь Леонтьєв в 1973 році отримав нобелівську премію з економіки.