1.Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця) і допускаючий операції (додавання, віднімання, множення та множення на скаляр).

Горизонтальні лінії в матриці звуть рядками, вертикальні — стовпцями.Матрицю, що складається з m рядків та n стовпців, називають матрицею m-на-n (або mn-матрицею), а m і n — її розмірністю.Елемент матриці A, що знаходиться на перетині i-го рядка з j-им стовпчиком, називають i,j-им елементом або (i,j)-им елементом A.

Додавання

Якщо дано дві матриці m-на-n A і B, можемо означити їх суму A + B як матрицю m-на-n, що утворюється додаванням відповідних елементів, себто, (A + B)[i, j] = A[i, j] + B[i, j]. Наприклад,

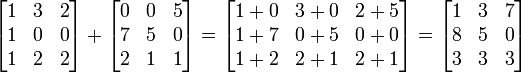
Множення на скаляр

Якщо дано матрицю A і число c, можемо означити множення на скаляр cA як (cA)[i, j] = cA[i, j]. Наприклад,

З цими двома операціями множина M(m, n, R) усіх матриць m-на-n з дійсними елементами є дійсним векторним простором розмірності mn.

Множення матриць

Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m-на-n (m рядків, n стовпчиків), а B — матриця n-на-p (n рядків, p стовпчиків), їх добуток AB є матрицею m-на-p (m рядків, p стовпчиків), що розраховується за формулою:(AB)[i, j] = A[i, 1] * B[1, j] + A[i, 2] * B[2, j] + ... + A[i, n] * B[n, j] для кожної пари i та j.

Наприклад,

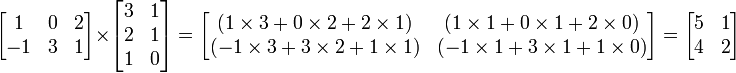
Це множення має такі властивості:

• (AB)C = A(BC) для всіх матриць A розмірності k-на-m, B розмірності m-на-n і C розмірності n-на-p (асоціативність).

• (A + B)C = AC + BC для всіх матриць A і B розмірності m-на-n і матриць C розмірності n-на-k (дистрибутивність).

• C(A + B) = CA + CB для всіх матриць A і B розмірності m-на-n і матриць C розмірності k-на-m (дистрибутивність).

Зауваження: комутативність має місце не завжди: для добутку певних матриць A і B може бути AB ≠ BA.

Матриці називають антикомутативними, якщо AB = −BA. Такі матриці є дуже важливими в представленнях алгебр Лі та в представленнях алгебр Кліффорда.

2. Визначником n-го порядку- називається число, яке дорівнює алгебраїчні сумі n!елементів матриці, кожний з яких є добутком n елементів матриці , взятих по одному з кожного стовпця і кожного рядка , прочому знак кожного члена визначається як (-1)^{a(j) ,} де a(j) – число інверсій в перестановці J з номерів стовпців елементів матриці , якщо при цьому номери рядків записані в порядку зростання:

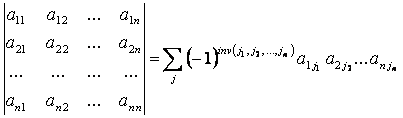
Де береться по всіх перестановках J.

Мінором (п-1)-го порядку M_ij матриці п-го порядку А називається детермінант (п-1)-го порядку матриці, утворений з матриці А викреслюванням і-го рядка і j-го стовпця, тобто:

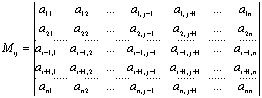
Означення 2: Алгебраїчним доповненням A_ij елемента a_ij матриці п-го порядку А, називається мінор (п—1)-го порядку M_ij, помножений на (-1)^i+j, тобто A_ij=(-1)^i+j·M_ij.

Так, наприклад, для вже наведеної матриці 3-го порядку маємо такі алгебраїчні доповнення елементів а₁₁ і а₃₂:

 

                        

ехай — квадратна матриця розміру в якій вибрано довільні рядків.

Тоді визначник матриці рівний сумі всіляких добутків мінорів -го порядку, розташованих в цих рядках, на їх алгебраїчні доповнення.

де підсумовування ведеться по всіх номерах стовпців

Число мінорів, по яких береться сума в теоремі Лапласа, рівне числу способів вибрати стовпців з , тобто біноміальному коефіцієнту .

Оскільки рядки і стовпці матриці рівносильні щодо властивостей визначника, теорему Лапласа можна сформулювати і для стовпців матриці.

Дана теорема має наступні застосування.

Розклад визначника по рядку (стовпцю)

Широко відомий окремий випадок теореми Лапласа — розкладання визначника по рядку або стовпцю. Він дозволяє представити визначник квадратної матриці у вигляді суми добутків елементів будь-якого її рядка або стовпця на їх алгебраїчне доповнення.

Нехай — квадратна матриця розміру . Нехай також заданий деякий номер її рядка або номер її стовпця При мінорами будуть самі елементи цього рядка чи стовпця.

Визначник може бути обчислений за формулами:

Розклад по -му рядку:

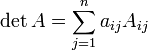
Розклад по -му стовпцю:

де — алгебраїчне доповнення до елемента, розташованого в рядку з номером та стовпці з номером .

3. Обернена матриця — матриця (позначається ), яка існує для кожної невиродженої квадратної матриці , розмірності , причому:

де одинична матриця.

Якщо для матриці існує , то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки — кожна оборотна матриця є невиродженою.

Властивості

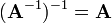• — операція обернення є інволюцією.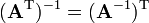

• — обернення транспонованої матриці

• — обернення спряженої матриці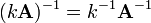

• для довільного коефіцієнта

• 

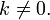
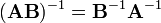
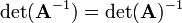• — визначник оберненої матриці.

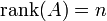• — ранг матриці дорівнює розміру матриці.

• Власні вектори матриці та її оберненої — збігаються, а власні значення є оберненими.

• Якщо потрібно розв'язати систему лінійних рівнянь 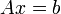, (b — ненульовий вектор) і існує, тоді 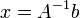. В протилежному випадку або розмірність простору розв'язків більше нуля, або їх немає зовсім.

Метод Гауса — Жордана використовується для розв'язання систем лінійних алгебраїчних рівнянь, знаходження оберненої матриці, знаходження координат вектора у заданому базисі, відшукання рангу матриці. Метод є модифікацією методу Гауса. Названий на честь Гауса та німецького математика та геодезиста Вільгельма Йордана.

Алгоритм

1. Обирається перша зліва колонка, що містить хоч одне ненульове значення.

2. Якщо верхнє число у цій колонці - нуль, то обмінюється увесь перший рядок матриці з іншим рядком матриці, де у цій колонці нема нуля.

3. Усі елементи першого рядка діляться на верхній елемент обраної колонки.

4. Від рядків, що залишились, віднімається перший рядок, помножений на перший елемент відповідного рядка, з метою отримання у якості першого елемента кожного рядка (крім першого) нуля.

5. Далі, повторюємо ці операції із матрицею, отриманою з початкової матриці після викреслювання першого рядка та першого стовпчика.

6. Після повторення операцій n-1 разів отримаємо верхню трикутну матрицю.

7. Віднімаємо від передостаннього рядка останній рядок, помножений на відповідний коефіцієнт, щоб у передостанньому рядку залишилась лише 1 на головній діагоналі.

8. Повторюємо попередній крок для наступних рядків. У результаті отримуємо одиничну матрицю і рішення на місці вільного вектора (над ним необхідно виконувати ті самі перетворення).

4. Ранг матриці — порядок найбільших відмінних від нуля мінорів цієї матриці (такі мінори називаються базисними).

Ранг системи векторів — найбільше число лінійно-незалежних векторів з цієї системи.

Зазвичай ранг матриці позначається ( ) чи .

• Ранг матриці не міняється при елементарних перетвореннях матриці (перестановці рядків або стовпців, множенні рядка або стовпця на відмінне від нуля число і при складанні рядків або стовпців).

• Теорема про базисний мінор: Рядки ненульової матриці на яких будується її базисний мінор є лінійно незалежними. Всі інші рядки матриці лінійно виражаються через них.

• Теорема про ранг матриці: Ранг матриці рівний найбільшому числу лінійно-незалежних рядків (або стовпців) матриці. Причому ранг по стовпцям збігається з рангом по рядкам.

• Теорема Кронекера-Капеллі: Система лінійних рівнянь має розв'язок тоді і тільки тоді, коли ранг матриці, складеної з коефіцієнтів при невідомих, не змінюється при додаванні до неї стовпця вільних членів (розширена матриця). Цей розв'язок єдиний, якщо цей ранг матриці дорівнює кількості невідомих.

Ранг матриці розмірності називають повним, якщо .

Система векторів має повний ранг вектори лінійно незалежні.