19. Модели непрерывного роста.

Пусть N(t)-численность вида или популяции в момент времени t, тогда скорость изменения численности опред-ся уравнением баланса для популяции dN(t)/dt=рождение-смертн*миграция (1) членов в правой части ур-я(1) требует моделирования рассматриваемой ситуации в простейшей модели исключают миграцию, а члены, обознчающие рождаемость и смертность пропорциональны N, dN/dt=bN-dN

(2); N₀=N(t₀)-нач численность популяции

Из формулы (20 следует, что, если b>d, т.е. рождаемость превышает смертность, то численность растет экспоненциально, если b<d, то численность убывает экспоненциально (эта модель была предложена Мальтусам в 18 веке ). В далекой перспективе должны существовать способы сдерживания экспоненциального роста. Ферхюмет в сер 19 в высказал догадку, что в случае оч быстрого роста численности населения должны включаться механизмы саморегуляции. Он предположил, что dN/dt=rN(1-N/k), r и k –некоторые положительные константы. Он назвал эту модель ”логическим ростом численности ” в этой модели число рождений на душу населения=r(1-N/k), т.е. зависит от N-число рождений на душу населения, const k-емкость среды, которая обычно определяется кол-вом доступных рес-ов, необходимых для поддержания жизни. Найдем стационарное состояние ур-я (3). Для этого Nr(1-N/k)=0, 1)N=0; 2)1-N/k=0, N=k

Т.о. существуют 2 стационарных(равновесных) состояния ур-я(модели) (3), N=0 и N=k

Состояние N=0 получается неустойчивым. dN/dt=rN(1-N/k) , dN/dt=rN это неустойчивое состояние N(t)=N₀e^rt Другое состояние равновесия N=k устойчиво.

dN/dt=r(N-N²/k)=r/k(kN-N²)=r/k(k-N)N/ емкость среды k определяет размер популяции находящейся в устойчивом стационарном состонии. Параметр r определяет скорость с которой этот размер популяции достигается, т.е. это мера динамики роста. Т.о. величина 1/r явл-ся масштабом времени ответа модели на любое изменение в популяции.

Ур-е (3) имеет след решение: (4) N₀=N(0)

Если e^rt велико, можно пренебречь 1 и k в знаменателе тогда: =k (5)

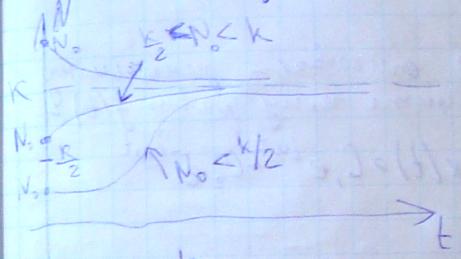Если N₀<k, то зависимость N(t) монотонно возрастает до k, если же N₀>k, то зависимость N(t) монотонно уменьшается до значения k. В случае когда N₀>k оказывается , что число рождений на каждого человека-это отрицательная вел-на. В действительности это означает, что число рождений+иммиграция <число смерти+ эмиграция.

Смысл ур-я (3) состоит в том, что для класса популяционных моделей с зависимым от плотности нас-я регуляторным механизмом явл-ся некоторым упрощением. И данное ур-е не должно восприниматься слишком буквально, как ур-е управляющее законами динамики численности населения. Не смотря на его совершенства время от времени это ур-е заново открывает и широко пропагандирует в качестве универсального закона

'' управляющего ростом численности населений'' Лагистическая модель (3) имеет 3 параметра N₀, k, r которые можно сопоставлять с реальными данными.

20. Методы укрощения сложных систем. Линеаризация.

К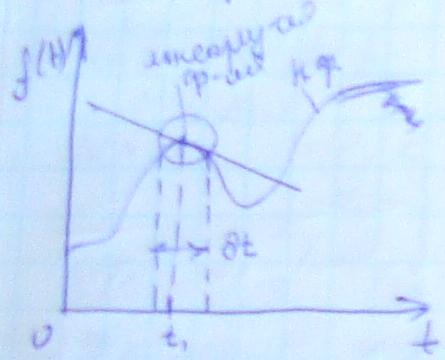 ак правило, сложная система описывается нелинейными математическими уравнениями. Часто найти аналитические решения таких уравнений бывает очень трудно, либо невозможно. В таких случаях используют численные методы анализа. Для выяснения общих закономерностей поведения системы часто используется также приближённые методы анализа, к которым относятся, в частности, метод линеаризации математических моделей.

f(t)-нелинейная функция

F(f(t), f '(t), t)=0-описывает динамику системы и выяснить, чему равно f(t) невозможно.

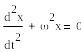
Линеаризация означает: проводим вблизи этой точки касательную, заменяющая в окрестности точки t исходную нелинейную функцию. Линеаризация происходит, если:

Геометр. смысл-это ур-е некот. ур-я f(t) в т. t1.

Если:

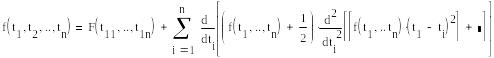
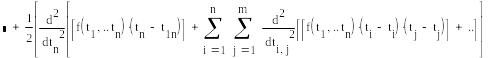
В сл. n-переменных линеар-я означает, что отбрасываются все линейные члены и исходную ф-цию n-переменных заменяют на лин. ф-цию.

Часто динамика системы описывается ур-м вида:

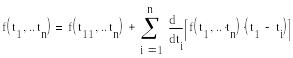
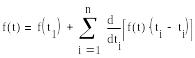
x-некот. переменная состояния системы, u-некот. ф-ция управления

x=x(t), u=u(t)

Линеаризация:

В общем сл., когда имеется n-переменных состояний динамика системы описывается след. системами ур-й:

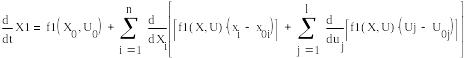
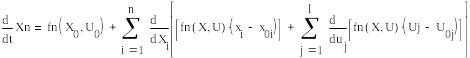
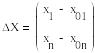
_{- независимая матрица Якоби}

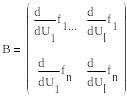
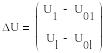
_{Линеариз. система в матричном виде записывается след. образом:}

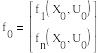
_{Часто при исследовании систем требуется выяснить её поведение вблизи стацион-х состояний:}

_{Чтобы найти стац. состояние системы нужно правую часть приравнять к 0: f(X,U)=0, где (X0,U0)-координаты стац. состояния. Если исследуется динамика системы вблизи стац. состояния, тогда f0=0. Поэтому линеариз. система в этом сл. примет вид:}

_{Чтобы найти устойчивость стац-х сост-й, необх. составить характеристическое ур-е. Пусть}

det (A-E)=0

_{E-единичная матрица}

-собственное число характерист. ур-я

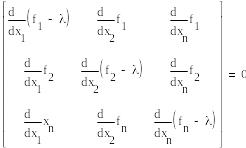
_{Всего n собственных значений. В общем сл., эти собств.значения явл-ся комплексными.}

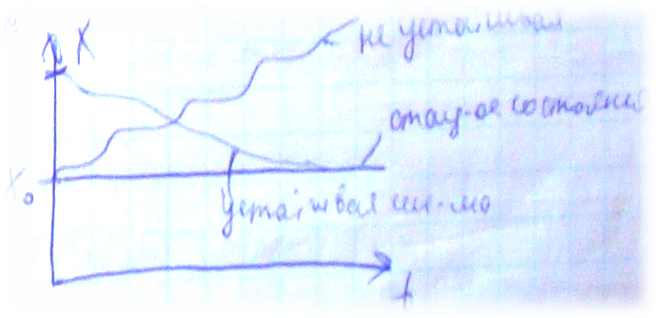
_{1)Если все действительные части собственных значений отрицательные, т.е. Re λi<0 для всех i, то система явл-ся устойчивой.}

_{2)Если хотя бы одно собст. значение имеет положит. действительную часть, т.е. Re λi>0 хотя бы для одного i, то система не устойчива.}

_{3)Если какие-либо собст. значения имеют действ. части, равные 0, т.е. Re λi=0 для некот. i, то требуются дополнительные исследования.}

_{4)Если все или некот. собст. значения имеют мнимые части ≠ 0для некот. i, то в системе могут возникнуть колебания.}