4. Деякі елементарні функції комплексної змінної та їх властивості

4.1. Лінійна функція

Лінійна функція має вигляд , де , – комплексні сталі.

Лінійна функція визначена на всій комплексній площині, однозначна і неперервна. Обернена їй функція також лінійна і однозначна. Похідна . Отже, лінійна функція аналітична, однолиста і здійснює конформне відобра­жен­ня на всій площині.

Лінійне відображення є перетворенням подіб­нос­ті, що зводить­ся до послідовної суперпозиції: а) повороту площини на кут ; 2) розтягування її в разів; 3) зміщення її вздовж вектора .

Лінійне відображення має кругову властивість: пряма переходить в пряму, а коло – в коло.

4.2. Степенева і коренева функції

Степенева функція з натуральним показником має вигляд , де .

Степенева функція визначена на всій комплексній площині, однозначна, неперервна. Похідна всюди не­перервна. Отже, степенева функція аналітична на всій комплексній площині.

Промінь відображається в промінь . Якщо точка належить сектору , різ­ним відповідають різні . Значить, функція є однолистою в цьому секторі. Указаний сектор відображається в -площину з розрізом по від’ємній дійсній півосі (рис.20).

К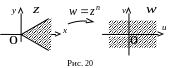 оренева функція має вигляд , де – неско­ротний правильний дріб: , .

Коренева функція (радикал) визначена на всій ком­плексній площині і багатозначна. Похідна всюди ви­значена і неперервна, крім . Тому ця функція аналітична на всій площині за винятком точки . Оскільки функція -значна, то для визначення єдиного образу при цьому відображенні необхідні додаткові умови. Функція стає однолистою на всій площині, якщо вважати значення функції додатним дійсним для додатного дійсного аргументу. Тоді -площина з розрізом по від’ємній дійсній півосі відображається на сектор .

4.3. Показникова функція

Показникова (експоненціальна) функція комплексної змін­ної визначається рівністю

.

На дійсній осі ця функція збігається з дійсною експонентою . Зберігається основне правило: при множенні експонент їх показники додаються . Справедливі також співвідношення: ; .

Модуль комплексної експоненти , а аргумент , . Отже, ця функція є періодичною з уявним періодом : .

Похідна комплексної експоненти дорівнює їй самій і всюди відмінна від нуля . Тому ця функція аналі­тична у всій комплексній площині і задає конформне відобра­ження. При цьому довільна горизонтальна пряма перетворюється у відкритий промінь, що виходить з початку координат, а довільний вертикальний відрізок довжиною переходить в коло з центром у початку координат.

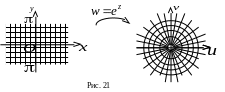
Через періодичність комплексної експоненти ві­до­браження буде однолистим у кожній горизонтальній смузі

, де .

Кожна така смуга відображається в -площину з вилученим початком координат (рис. 21). При цьому координатна сітка декартової системи на -площині перетворюється в сітку по­лярних координат на -площині.