3.4. Геометричний зміст модуля й аргументу похідної. Поняття про конформне відображення

Нехай аналітична функція відображає область -площини на область -площини (рис. 17), при цьому точці відповідає точка , а дуга довільної гладкої кривої переходить у дугу відповідної гладкої кривої .

Нехай похідна скінченна і відмінна від нуля , а прямує до нуля вздовж кривої .

Л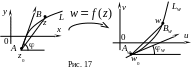 окальним коефіцієнтом розтягу в точці називається гра­ниця відношення довжин дуги-образу і дуги-прообразу : .

Замінюючи відношення дуг відношенням їх хорд, можна одержати:

.

Геометричний зміст модуля похідної: оскільки границя не залежить від характеру прямування до нуля (від вибору кривої ), то локальний коефіцієнт розтягу в точці під дією аналітичної функції в усіх напрямах однаковий і дорівнює модулю похідної (властивість сталості розтягу)..

Нехай і – кути нахилу дотичних відповідно до кривої у точці і до кривої у точці .

Локальним коефіцієнтом повороту в точці називається різниця кутів нахилу дотичних відповідно до дуги-образу і дуги-прообразу : .

Оскільки кут нахилу дотичної дорівнює границі кута нахилу січної, , а з диференційовності випливає неперервність, то

.

Геометричний зміст аргументу похідної: локальний коефіцієнт повороту в точці під дією аналітичної функції не залежить від вибору кривої і дорівнює аргументу похідної . Якщо через точку провести дві різні лінії, то кут між образами дорівнюватиме куту між прообразами як за величиною, так і за напрямом (властивість консерватизму (зберігання) кутів).

Відображення, що має властивості консерватизму кутів та сталості розтягу, називається конформним.

Отже, аналітична функція здійснює конформне відображення у кожній точці , де і .

Відображення називається конформним в області , як­що воно конформне в кожній точці цієї області.

Зауваження 1. При конформному відображенні нескінченно малі фігури перетворюються в подібні собі нескінченно малі фігури. Проте від точки до точки значення коефіцієнтів і змінюються, тому форми скінченних фігур змінюються, хоча зберігаються кути між лініями.

Основна задача конформного відображення: знайти аналітичну функцію , яка однолисто і конформно відображає задану область -площини на область -площини. Якщо ці області однозв’язні та їх межі складаються більш ніж з однієї точки, то ця задача має нескінченну кількість розв’язків. Для виділення конкретного розв’язку треба задати додаткові умови, наприклад, образи однієї внутрішньої та однієї межової точки області .

Зауваження 2. Викликає значний інтерес також більш проста задача: знайти образ однозв’язної області при заданому відображен­ні аналітичною функцією . Правило її розв’язання: 1) знаходимо образ межі області , при цьому лі­нія розбиває -площину на частини; 2) щоб вибрати з них відповідну частину , треба скористатися принципом збереження напряму обходу: якщо задана орієнтація межі об­ласті , то при відображенні образ повинен залишатися по ту ж сторону від межі, що й прообраз .

Приклад 1. Визначити, яка частина комплексної площини розтягується і яка стискається при відображенні ?

Розв’язання.  Знайдемо похідну:

.

Обчислимо її модуль: .

Оскільки коефіцієнт лінійного розтягу дорівнює модулю похідної, то область, де , стискається, а область, де , розтягується. Знайдемо межову лінію:

; ; ;

; .

Т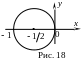 аким чином, межею служить ко­ло з центром у точці і ра­діусом (рис. 18). Вну­трішня частина круга стискається, а зовнішня – розтягується.

Приклад 2. Знайти образ квадрата (рис. 19)

при відображенні функцією .

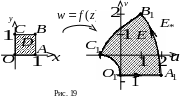
Розв’язання. Знаходимо дійсну й уявну частини заданої функції:

; ; .

Визначаємо образи сторін квадрата:

1)  , тому ; . Образом відрізка служить відрізок , паралельний осі .

2)  , тому ; . Тоді ; . Образом відрізка служить дуга параболи .

3)  , тому ; . Тоді ; . Образом відрізка служить дуга параболи .

4)  , тому ; . Тоді ; . Образом відрізка служить дуга параболи .

Контур розбиває -площину на дві частини: внутрішню і зовнішню (рис. 19). Користуючись відповідністю кутових межових точок і принципом збереження напряму обходу контуру, визначаємо, що образом квадрата служить внутрішня область .