5.3. Інтегральна формула Коші та її наслідки

Інтегральна теорема Коші відкриває можливість визначення значень аналітичної функції всередині області через її значення на межі цієї області.

Н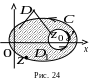 ехай функція аналітична в однозв’язній області , що обмежена кусково-гладким контуром і неперервна в замкненій об­ласті (рис. 24). Для довільної фіксованої внутріш­ньої точки області допоміжна функція є аналі­тичною в цій області, крім хіба що точки . Обведемо точ­ку колом з центром у цій точці та радіусом таким, що все коло лежить всередині області . Тоді допоміжна функція буде аналітичною у двозв’язній області між контурами і . За теоремою Коші

; .

Тоді

.

Із неперервності підінтегральної функції випливає, що останній інтеграл прямує до нуля при і при стає рівним нулю. Дістаємо інтегральну формулу Коші (інтеграл Коші)

.

Зауваження 1. У випадку багатозв’язної області інтегрування треба проводити по повній межі у додатному напрямі.

Зауваження 2. Оскільки – довільна точка області аналі­тич­ності, то індекс можна опустити, а межові точки позначити через . Тоді формула Коші (інтеграл Коші) набуває вигляду

.

Інтеграл Коші виражає значення аналітичної функції в довільній точці через її значення на довіль­ному контурі , що лежить в області аналітичності функції і містить точку всередині. В цей інтеграл змінна входить як параметр.

Наслідок 1. 

Зауваження 3. Нехай функція – аналітична в області з межею і неперервна в замкненій об­ласті . Нехай – довільна точка межі . Тоді в силу неперервності функції до самої межі з наслідку 1 випливає:

; .

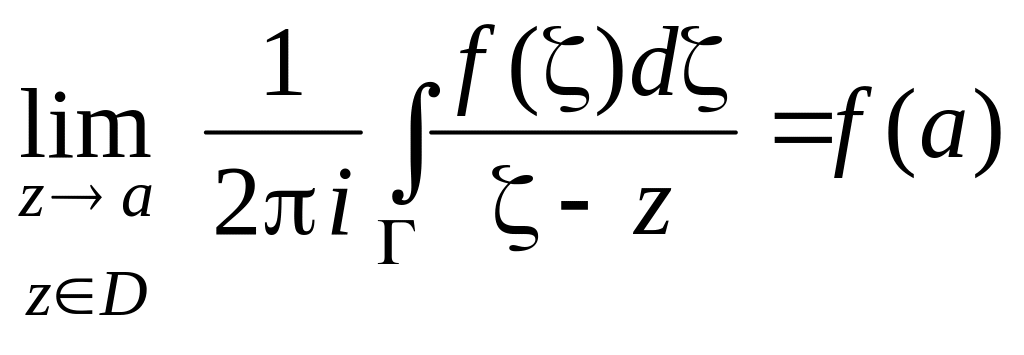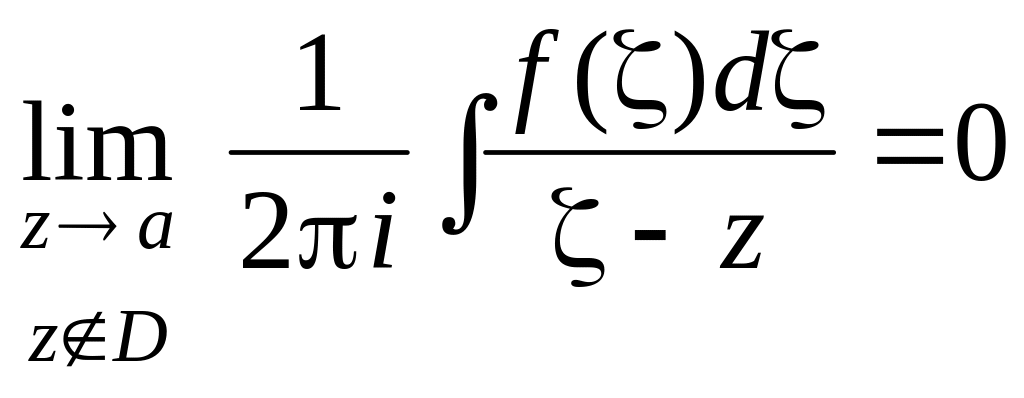Таким чином, на межі області функція має стрибок, що дорівнює – значенню цієї функції на межі.

Наслідок 2. Нехай функція – аналітична в області з межею і – довільна внутрішня точка цієї області. Тоді функція нескінченно разів диференційовна, причому

; .

Ці співвідношення одержуються диференціюванням інтеграла Коші, де похідна по параметру береться від підінтегральної функції.

Теорема і формула Коші знаходять широке застосування при обчисленні інтегралів по замкнутих контурах.

Приклад. Обчислити інтеграл по вказаному замкненому контуру :

а) ; б) ; в) .

Розв’язання. Підінтегральна функція всю­ди аналітична за винятком двох особливих точок і .

а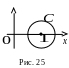 ) Особлива точка не входить всередину області , обмеже­ної контуром (рис. 25). У підінтегральному ви­разі виділимо функцію , що аналітична в області . Тоді для обчислення інтеграла можна скористатися формулою Коші для першої похідної:

.

б ) Обидві особливі точки і не входять всередину області , обмеже­ної контуром (рис. 26). Підінтегральна функція аналітична в цій області, тоді за теоремою Коші

.

в ) Обидві особливі точки і входять всередину області , обмеже­ної контуром (рис. 27). Побудуємо кола і з центрами відповідно в точках і достатньо малих радіусів так, щоб вони не перетинались ні з контуром , ні між собою. У тризв’язній області, обмеженій ззовні контуром , а зсередини – колами і , під­інтегральна функція аналітична. За теоремою Коші для складеного контуру

,

де обхід всіх контурів здійснюється проти годинникової стрілки.

У підінтегральному ви­разі першого доданка виділимо фун­кцію , що аналітична в області, обмеженій контуром . Тоді за формулою Коші:

.

Другий доданок не залежить від вибору контуру , що охоплює тільки одну особливу точку , то­му його значення співпадає з обчисленим в пункті а). Отже,

.

Таким чином,

.