Приклади електромеханічних пристроїв

Електричний генератор постійного струму (рис. 1.17).

Д ана аперіодична ланка має такі параметри передаточної функції:

,

де – константа, яка залежить від конструктивних особливостей генератору, ; – частота обертання якоря, ; – коефіцієнт нахилу лінеаризованої

характеристики намагнічування генератору, ; – кількість витків обмотки збудження, які приходяться на один полюс; – опір обмотки збудження, .

Постійна часу генератора: , де – індуктивність обмотки збудження, .

Термопара (рис. 1.18). Даний прилад є аперіодичною ланкою, якщо вхідна і вихідна величини такі:

– температура, ;

– напруга на контактах термопари, .

залежить від матеріалу термопари, наприклад

Метали
платинородій-платина	6,4·10-3
хромель-алюмель	41·10-3
хромель-копель	69,5·10-3
залізо-константан	57,5·10-3
мідь-константан	47,5·10-3

Постійна часу визначається так:

,

де – теплоємкість термометричного тіла, Дж/К; – коефіцієнт тепловіддачі, Вт/(м²·град); – поверхня корпусу термопари, .

Приклади чотирьохполюсників

Схема	K	T
	1
	1

Чотирьохполюсники на активних елементах

Схема	K	T

Реальна диференцююча ланка

Мета: зняти часові характеристики, виконати математичний аналіз та провести ідентифікацію реальної диференцюючої ланки.

Вихідні дані для настроювання параметрів стенду сул-3

Вхідна напруга, В	G	0,5
Коефіцієнт підсилення	k	2
Постійна часу (1 варіант), с	T1	1
Постійна часу (2 варіант), с	T2	0,5
Постійна часу для ідентифікації, с	TX	TX2

Передаточна функція має вигляд:

Диференційне рівняння ланки:

Реальна диференцююча ланка – це є послідовне з’єднання ідеального диференцюючої ланки та інерційної ланки першого порядку.

Із взаємної відповідності динамічних характеристик відомо, що перехідна функція може бути знайдена як зворотне перетворення Лапласа частки, діленим якої є передаточна функція, а дільником – оператор р. Тобто:

Знайдемо перехідну функцію. Для цього отриманий дріб розкладемо методом невизначених коефіцієнтів на прості дроби:

З таблиці зворотного перетворення Лапласа видно, що

Перетворивши отриману формулу, знаходимо h(t):

, або

Застосувавши методи аналітичної геометрії, можна впевнитися в тому, що дотична до кривої в точці відтинає на осі часу відрізок, що дорівнює постійній часу .

Знайдемо тепер імпульсну перехідну функцію. Як відомо, вона представляє собою похідну від перехідної функції, тобто:

Аналогічно, можна довести, що дотична до кривої в точці відтинає на осі часу відрізок, що дорівнює постійній часу .

Амплітудно-фазова характеристика може бути отримана шляхом підстановки в передаточну функцію .

Звідси видно, що дійсна і уявна частотні характеристики дорівнюють відповідно:

;

Амплітудно-фазова характеристика має вигляд півкола, із центром на дійсній осі в точці . Для доведення цього, піднесемо до квадрату обидва вирази та складемо їх:

Звідси доповнивши до квадрату, отримаємо рівняння кола:

Радіус дорівнює , а центр знаходиться в точці .

Амплітудно-частотна характеристика представляє собою модуль вектора амплітудно-фазової характеристики і знаходиться за формулою:

Підставивши в дану формулу вирази для та , одержимо:

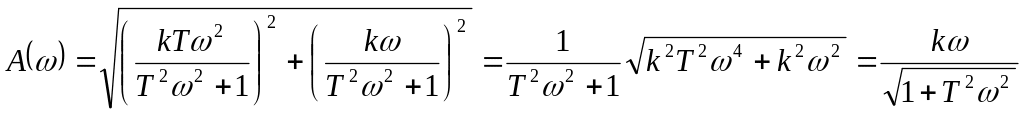
Як бачимо при маємо горизонтальну асимптоту до графіка функції АЧХ: .

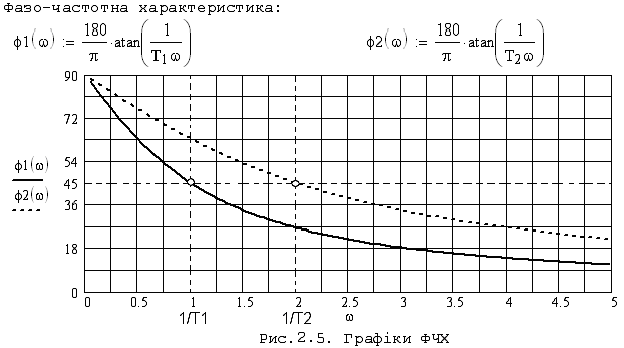
Фазочастотна характеристика може бути отримана за формулою:

Чим більша частота вхідного сигналу, тим менше випередження по фазі вихідного сигналу по відношенню до вхідного. При частоті спряження вихідний сигнал випереджує вхідний на .

Логарифмічна амплітудно-частотна характеристика описується виразом:

Асимптотична логарифмічна амплітудно-частотна характеристика характеризується тим, що її перша асимптота при ( ) представляє пряму, яка має нахил :

,

а при ( ) представляє паралельну осі декад пряму: