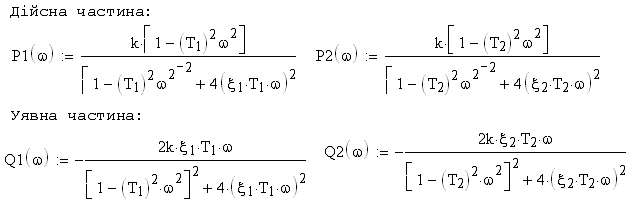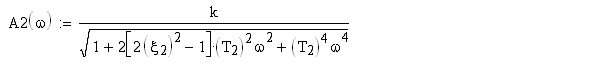Вихідні дані для настроювання параметрів стенду сул-3

Вхідна напруга, В	G	2
Коефіцієнт підсилення	k	1
Постійна часу (1 варіант), с	T1	1
Постійна часу (2 варіант), с	T2	0,5
Постійна часу для ідентифікації, с	TX	TX3

Щоб система була коливальною в обох випадках, тобто при і при візьмемо Виходячи з цього, одержимо коефіцієнти приведеної передаточної функції:

T1	ξ1	T2	ξ2
1,12 с	0,25	0,35 с	0,79

Передаточна функція має вигляд:

Диференційне рівняння ланки:

Із взаємної відповідності динамічних характеристик відомо, що перехідна функція може бути знайдена як зворотне перетворення Лапласа частки, діленим якої є передаточна функція, а дільником – оператор р. Тобто:

Знайдемо перехідну функцію. Для цього отриманий дріб розкладемо методом невизначених коефіцієнтів на прості дроби, але при цьому визначимо комплексні корені характеристичного рівняння:

Тут – коефіцієнт затухання; – кругова частота затухаючих коливань, рад/с.

Маємо:

З таблиці зворотного перетворення Лапласа видно, що

Перетворивши отриману формулу, знаходимо h(t):

Застосуємо формулу Ейлера:

де .

За теоремою Вієта для приведеного характеристичного квадратного рівняння можемо стверджувати, що:

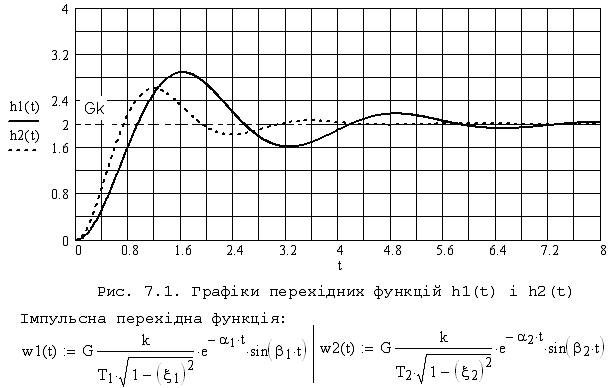
Одержали перехідну функцію в остаточному вигляді:

.

Як бачимо період затухаючих коливань дорівнює:

Чим більше коефіцієнт ξ і менше постійна Т, тим швидше затухають коливання. Якщо коефіцієнт демпфірування ξ=0, то на виході ланки після подачі одиничного ступінчатого збурення виникають незатухаючі коливання з частотою .

Швидкість затухання коливальних процесів оцінюється ступенем затухання:

,

де і – дві сусідні амплітуди над усталеним значенням перехідної функції.

З рівняння перехідної функції легко отримати верхню вітку огинаючої :

Оскільки амплітуди і відповідають деяким моментам часу і , то маємо:

Підставивши в дану формулу значення і , одержимо степінь затухання у вигляді:

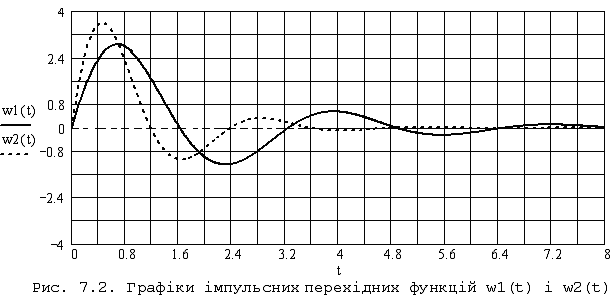
Знайдемо тепер імпульсну перехідну функцію. Як відомо, вона представляє собою похідну від перехідної функції, тобто:

,

де кут . З цього витікає наступний вираз для імпульсної перехідної функції:

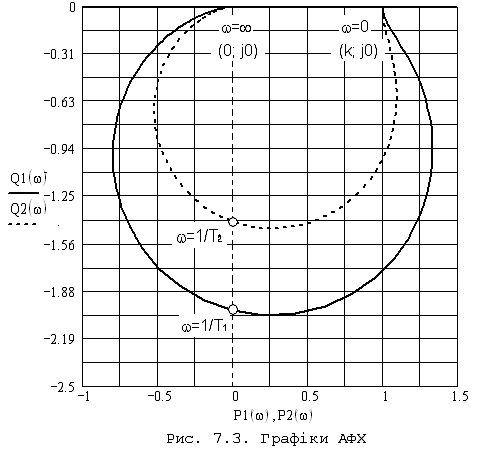
Амплітудно-фазова характеристика може бути отримана шляхом підстановки в передаточну функцію .

Звідси видно, що дійсна і уявна частотні характеристики дорівнюють відповідно:

; .

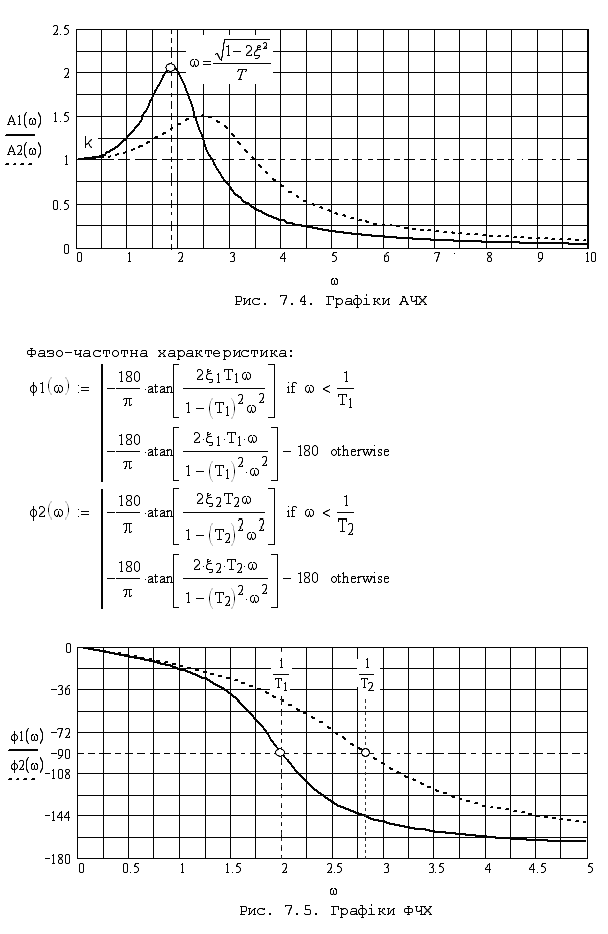
Амплітудно-частотна характеристика представляє собою модуль вектора амплітудно-фазової характеристики і знаходиться за формулою:

Підставивши в дану формулу вирази для та , отримаємо:

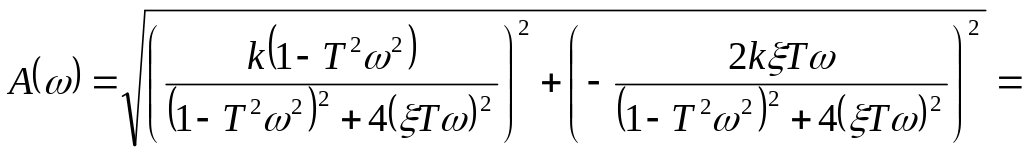
Проаналізувавши графік функції , можна побачити, що коливальна ланка має властивості фільтру низьких частот, тобто гармонічні сигнали малої частоти пропускаються ланкою добре, а сигнали великої частоти зазнають сильного ослаблення.

Знайдемо точку максимуму амплітудно-частотної характеристики:

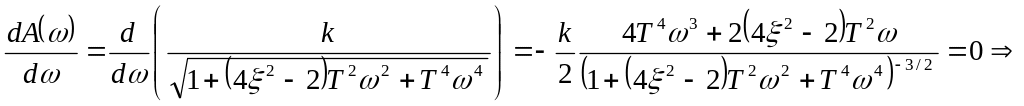
Фазочастотна характеристика може бути отримана за формулою:

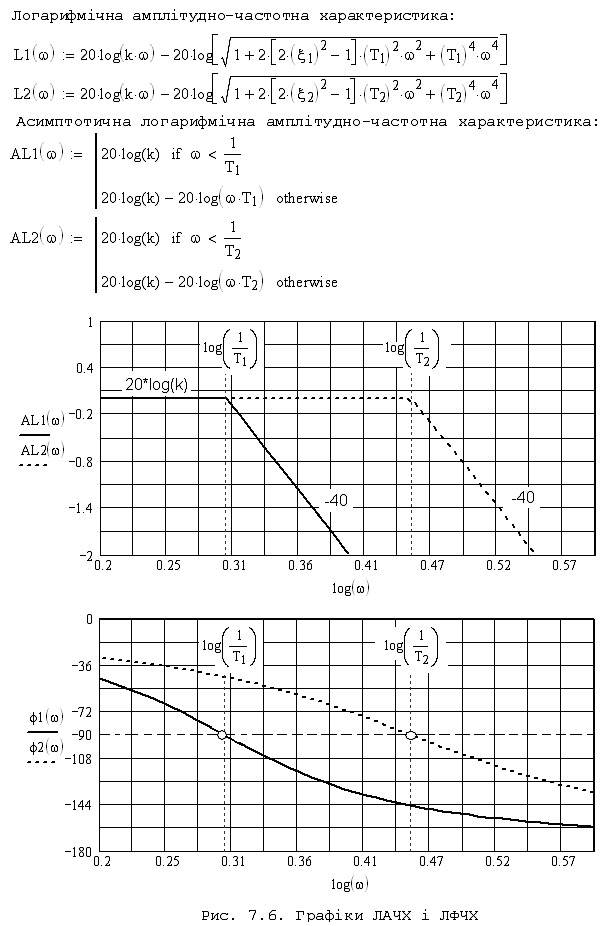
Логарифмічна амплітудно-частотна характеристика описується виразом:

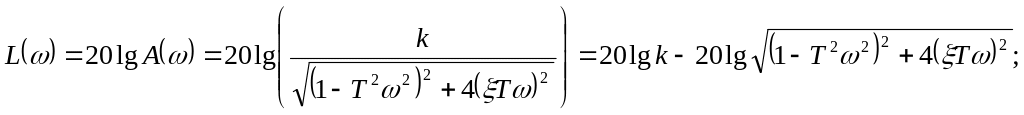
Асимптотична логарифмічна амплітудно-частотна характеристика характеризується тим, що її перша асимптота при ( ) представляє пряму паралельну осі :

,

а при ( ) представляє пряму, яка має нахил :

Частота спряження: .