1.10. Числовий n - вимірний простір

Множину усіх n - вимірних векторів

з дійсними [комплексними] елементами позначають через і називають дійсним [комплексним] n - вимірним простором.

Властивості дій 1 – 9 числового n - вимірного простору (що подані нижче) випливають з відповідних властивостей 1 – 8 додавання і множення матриць на числа:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. .

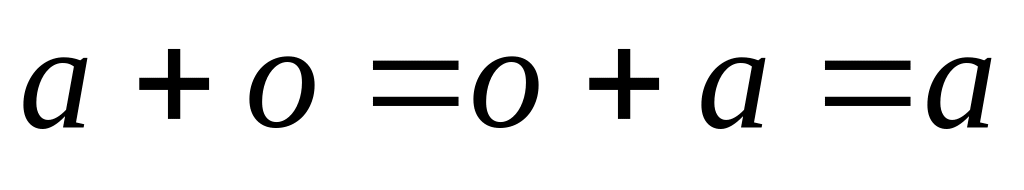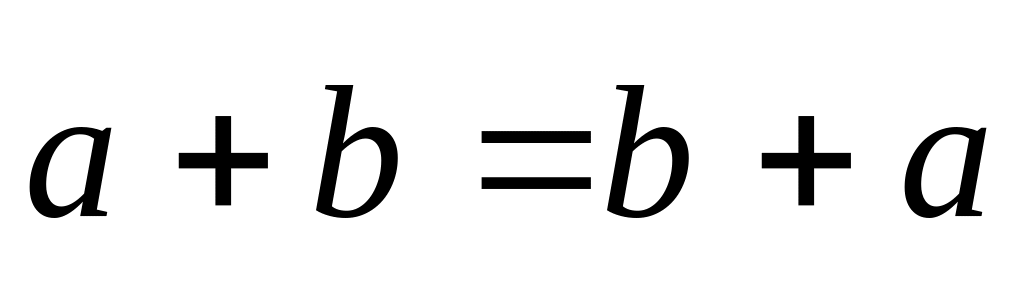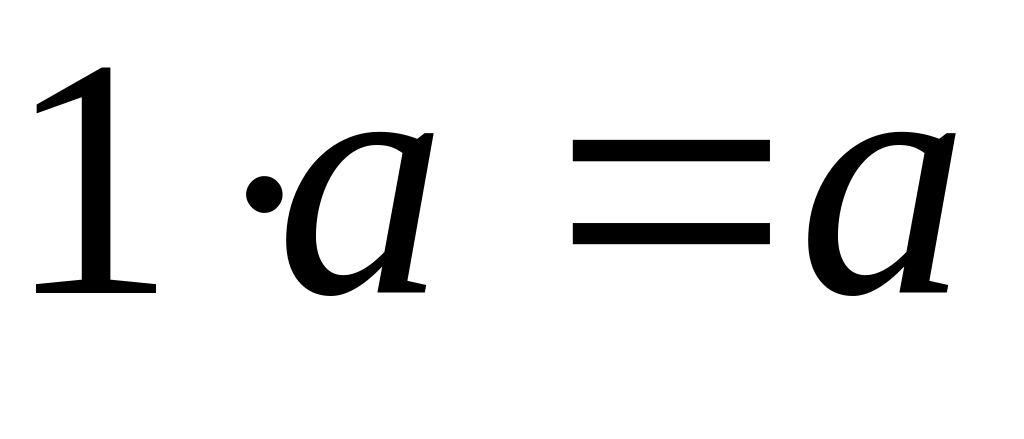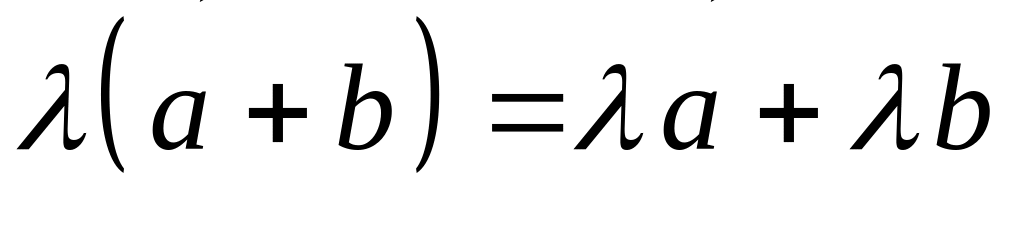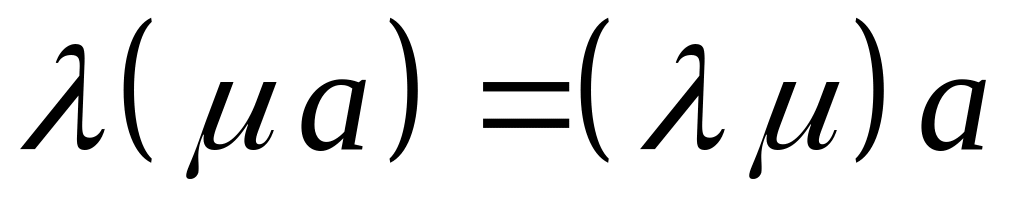(для довільних і ).

Лінійною комбінацією векторів називається вектор , де – числа.

В числовому n - вимірному просторі кожен вектор можна представити у вигляді лінійної комбінації векторів

де

Далі всюди ми використовуватимемо позначення тільки для вказаних векторів.

1.11. Подібні матриці

Будемо говорити, що квадратна матриця А порядку n є подібною до квадратної матриці С того ж порядку, якщо існує невироджена квадратна матриця Х порядку n така, що

В цьому випадку пишуть наступне: ~ .

Властивості подібності:

1. ~ (рефлексивність).

Справді,

2. Якщо ~ 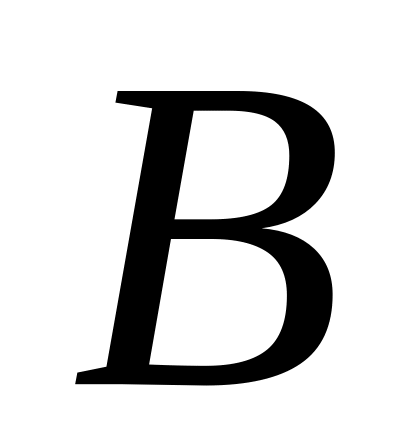, то ~ (симетричність).

Справді, якщо , то , бо

3. Якщо ~ і ~ , то ~ .

Справді, якщо ~ і ~ , то існують такі що , . Тоді , тобто .

Класом подібних матриць будемо називати всі матриці, що є подібними до даної матриці .

1.12. Вправи

1. Матрицю подати, як лінійну комбінацію матриць:

, , , ,

, , , ,

.

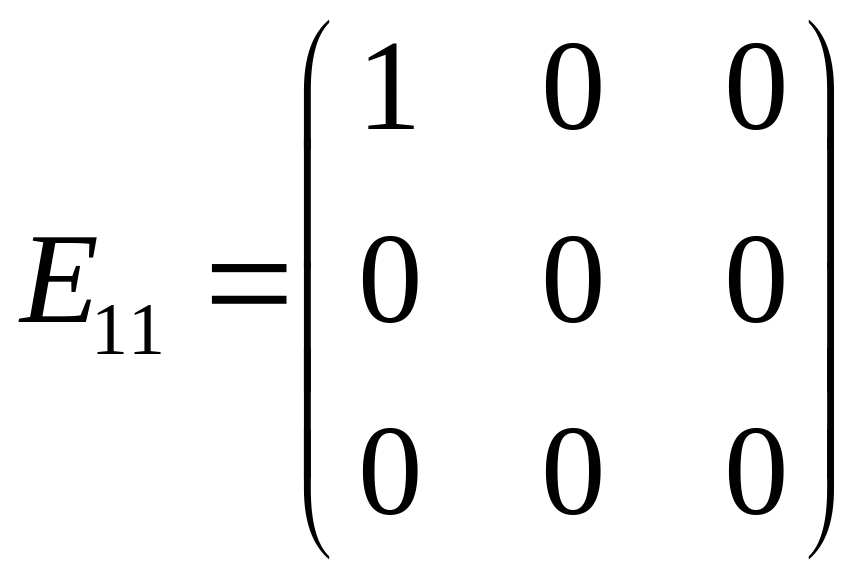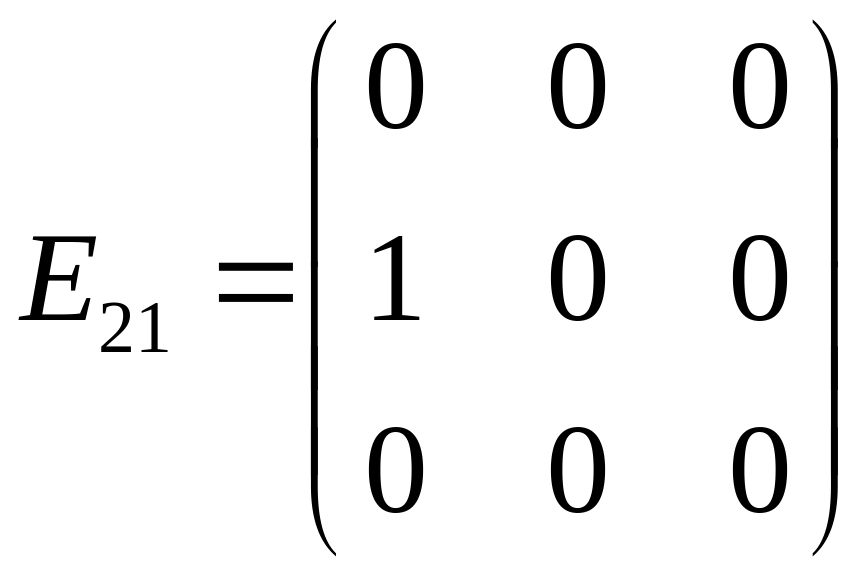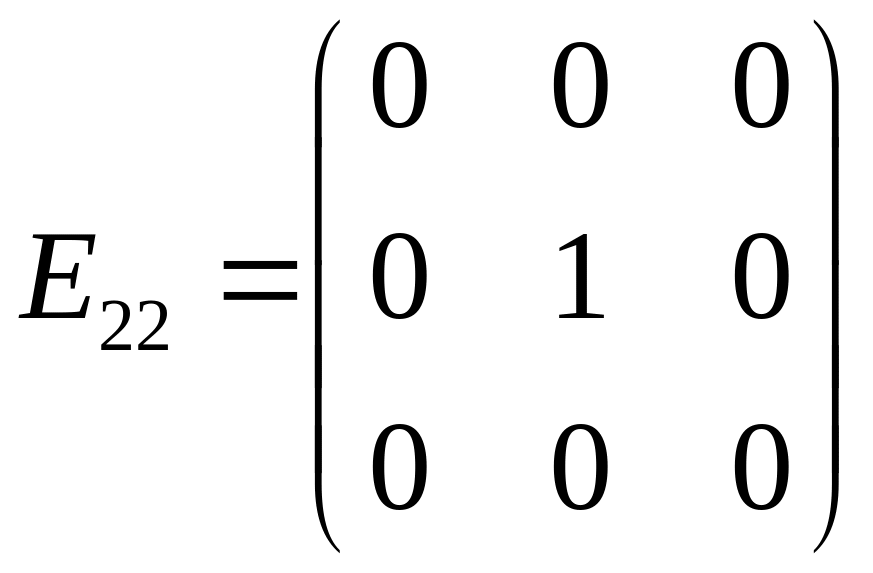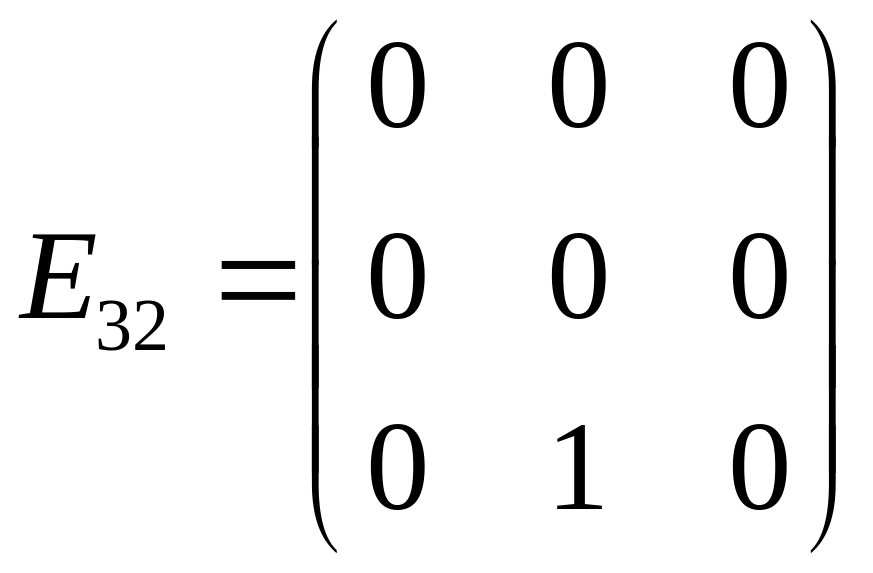2. Нехай . Чи обов’язково ?

3. Обчислити , якщо .

4. Коли справджуються рівності і .

5. Довести, що добуток двох симетричних матриць є симетричною

матрицею тоді й тільки тоді, коли ці матриці комутують.

6. Квадратна матриця називається кососиметричною, якщо .

Довести, що всяку квадратну матрицю можна представити як суму

симетричної та кососиметричної.

7. Обчислити

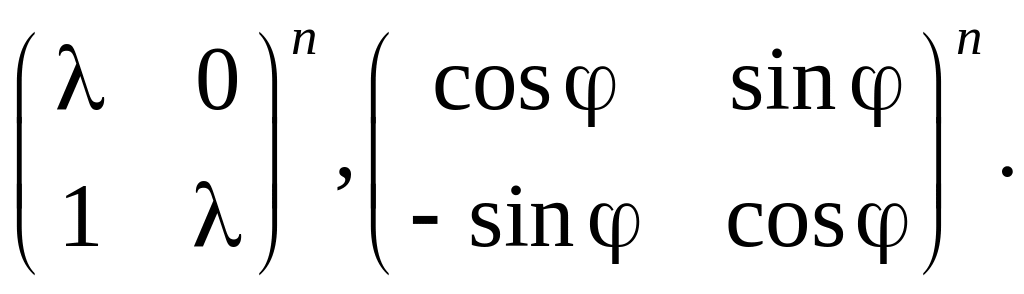
8. Довести: якщо , то обидві матриці квадратні та однакового

порядку.

9. Довести формулу .

10. Довести, що добуток двох верхніх (нижніх) трикутних матриць

однакового розміру є верхньою (нижньої) трикутною матрицею.

Розділ 2. Системи лінійних рівнянь

2.1. Система двох лінійних рівнянь з двома невідомими

Нехай маємо систему двох лінійних рівнянь з двома невідомими

(1)

В даному пункті розглядатимемо лише такі системи.

Розв’язком такої системи називається вектор , де – числа, для якого мають місце такі числові рівності:

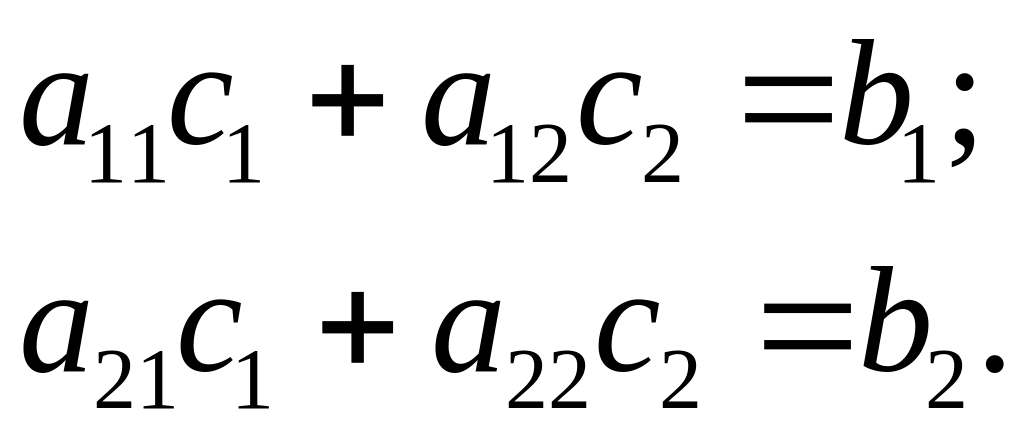
Система може не мати розв’язків, може мати єдиний розв’язок, або мати більше одного розв’язку.

Приклади:

1).

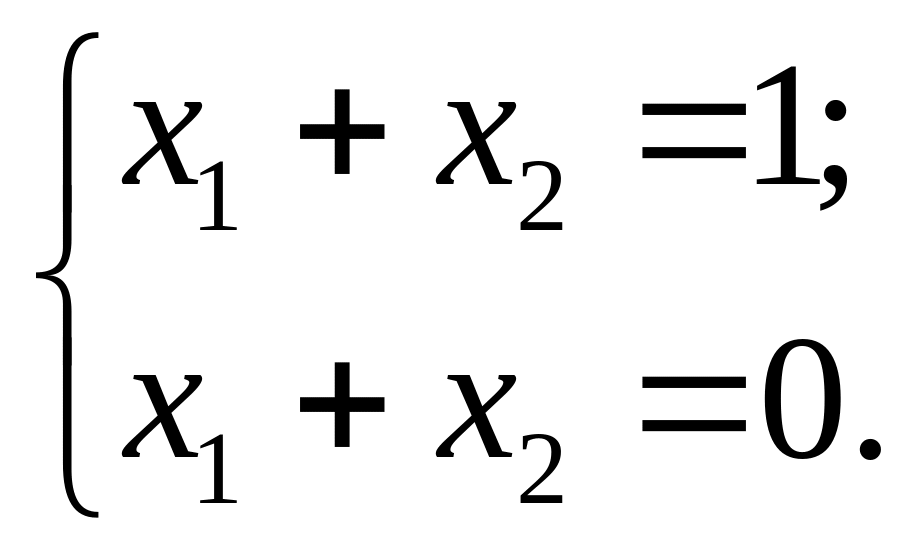
Дана система розв’язків не має.

2).

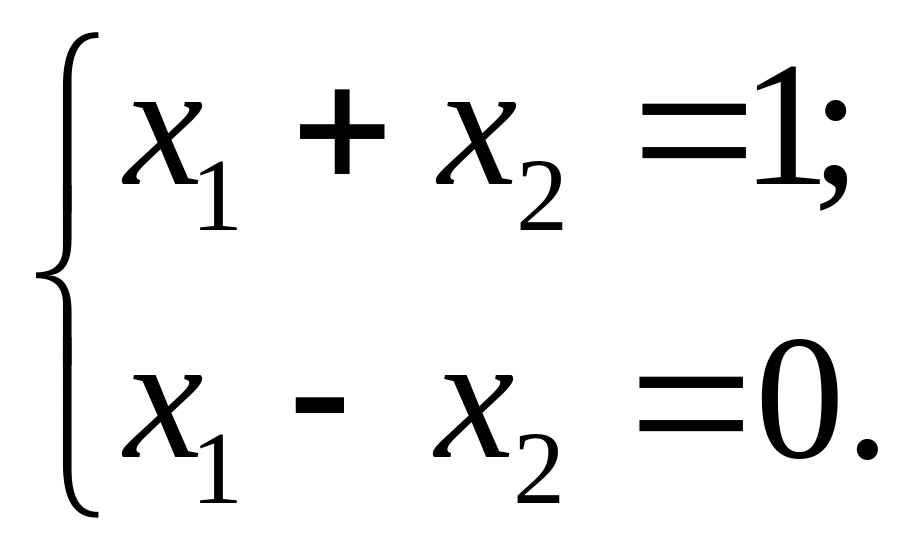
Дана система має єдиний розв’язок

3).

Дана система має безліч розв’язків де – довільне число.

Справді, і для довільного числа .

Дві системи рівнянь називаються рівносильними (еквівалентними), якщо вони мають однакові множини розв’язків. Система рівнянь називається сумісною, якщо вона має хоча б один розв’язок.

Система рівнянь називається несумісною, якщо вона не має жодного розв’язку, тобто множина розв’язків є порожня множина Ø.

Матриця називається матрицею системи (1). Систему (1) зручно записувати в матричному вигляді

(2)

де .

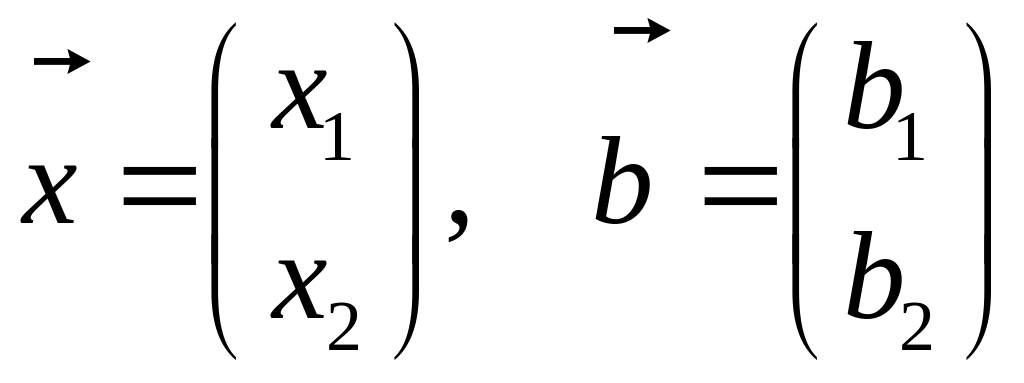Форму (2) запису системи (1) називають матричною. Крім такої форми запису, зручно використовувати запис у вигляді розширеної матриці:

, (3)

а також у векторній формі:

(4)

де

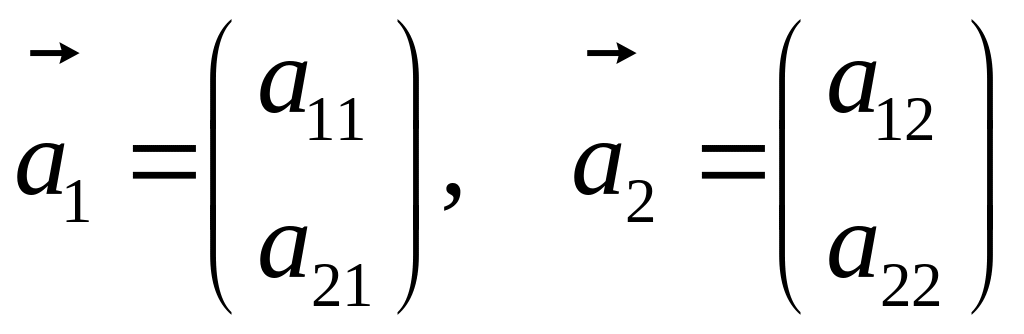– стовпці матриці .

Доведемо ряд важливих тверджень про розв’язки систем двох лінійних рівнянь з двома невідомими.

Лема 1. Якщо матриця є неособливою, то система (1) має єдиний розв’язок.

Доведення. Оскільки матриця є неособливою, то для неї існує обернена матриця .

Зрозуміло, що вектор – розв’язок системи (1). Справді, .

Покажемо, що це єдиний розв’язок системи (1). Справді, нехай - якийсь розв’язок системи (1). Тоді . Тоді , тобто . Це показує, що .

Лему доведено.

Лема 2. Якщо матриця є особливою, то система має ненульові розв’язки.

Доведення.

1). Нехай А ­­– нуль-матриця, тоді

Отже, - ненульовий роз’язок системи

2). Нехай А – не є нуль-матрицею. Тому не всі дорівнюють нулю.

Зрозуміло, що

і

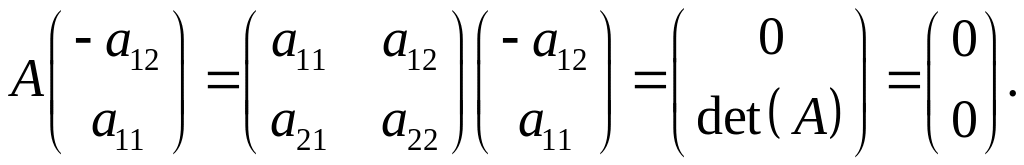
Оскільки не всі дорівнюють нулю, то з останніх двох рівностей випливає, що система має ненульові розв’язки.

Лему доведено.

Теорема. Система (1) має єдиний розв’язок тоді і тільки тоді, коли матриця цієї системи неособлива.

Доведення. З леми 1 випливає, що якщо А неособлива, то система (1) має єдиний розв’язок.

Навпаки. Нехай система (1) має єдиний розв’язок Покажемо, що тоді система має теж єдиний розв’язок (нуль-вектор).

Справді, припустимо, що ненульовий вектор 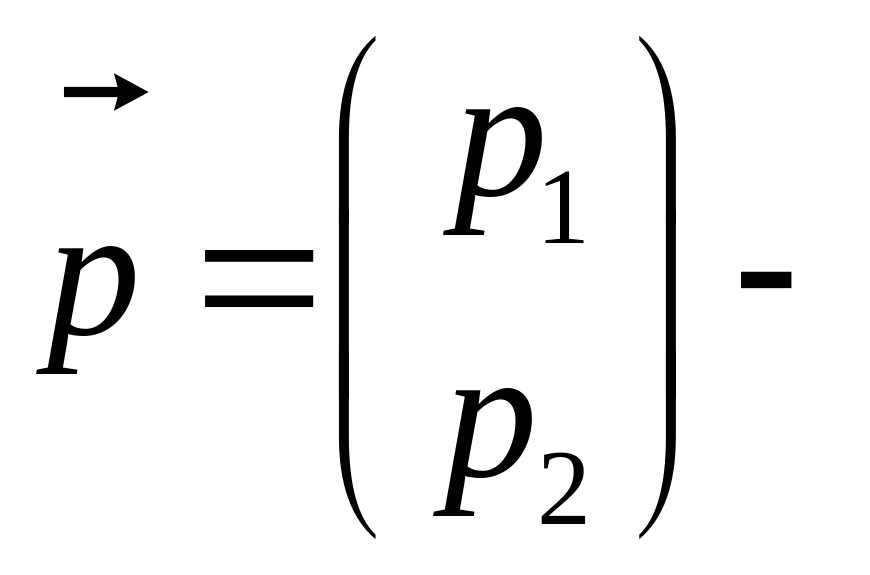розв’язок . Тоді – розв’язок системи (1). Справді, Зрозуміло, що , бо

Отже, система (1) має принаймні два різні розв’язки. Суперечність.

Отже, наше припущення хибне. Тому має лише один розв’язок. За лемою 2 А – неособлива матриця.

Теорему доведено.

Наслідок. Система , де , 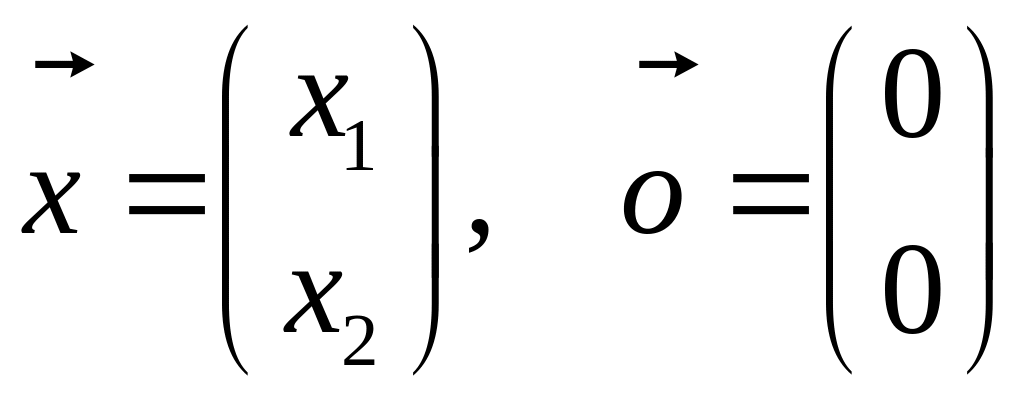має лише нульовий розв’язок тоді і тільки тоді, коли .