31.Еліпс: означення, рівняння, графік, вершини, півосі, фокуси

Множина точок площини, для яких сума відстаней від двох заданих точок, що називаються фокусами, є величина стала й така, що дорівнює 2а і більша, ніж відстань між фокусами, називається еліпсом.

Рис. 2.16

На рис. 2.16 зображено F₁ (–c, 0), F₂ (c, 0) — фокуси еліпса, М (х, у) — точка множини, яка задовольняє означення, тобто причому 2с < < 2a  a > c.

Тоді

(2.20)

канонічне рівняння еліпса, де b² = а² – с².

Розглянемо геометричний зміст параметрів, що входять в рівняння (2.20). Якщо х = 0, у =  b, тобто точки (0, b) і (0, – b) є точками перетину еліпса з віссю Оy. Відрізок завдовжки b називають малою піввіссю еліпса. При у = 0, х =  а і відповідно (а, 0); (– а; 0) є точками перетину еліпса з віссю Ох. Відрізок завдовжки а — велика піввісь еліпса. З парності виразу (2.20) за х і за у випливає симетрія еліпса відносно осей Ох і Оу. На рис. 2.16 зображено еліпс.

Вершинами еліпса є точки його перетину з осями координат:

з віссю Ох: у=0 , х^2=a^2, x=+-a

з віссю Оу: х=0, , y^2=b^2, y=+-b

Ексцентриситет еліпса — це відношення ; за означенням с < a і [0, 1). Оскільки то . З останньої рівності випливає геометричний зміст ексцентриситету, який полягає в тому, що він характеризує ступінь витягнутості еліпса. Так, при маємо коло, якщо  наближається до одиниці, то відношення довжини півосей еліпса стає малим, тобто еліпс витягується вздовж осі Ох.

Дві прямі, рівняння яких , називаються директрисами еліпса. Для еліпса 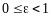і відношення , директриси еліпса — це дві прямі, що розміщені симетрично відносно осі Оу і проходять зовні еліпса.

32.Гіпербола: означення, рівняння, графік, спряжена гіпербола.

Гіперболою наз. множина точок площини, для яких модуль різниці відстаней від двох заданих точок (фокусів), є величина стала, яка дор. 2а і менша за відстань між фокусами.

у=+-b/a*x – асимптоти гіперболи.

АА1=2а дійсна вісь гіперболи

ВВ1=2в уявна вісь гіперболи

АА1 по х

Е=2с/2a=c/а екстренциситет

х=+-а/b директриса гіперболи

b2=c2-a2.

33.Парабола: означення, рівняння, графік, вершина, фокус.

Множина то­чок площини, що містяться на однаковій відстані від даної точки фокуса і даної прямої, яка не проходить через фокус і називається директрисою, є парабола.

За означенням r = d, отже

:

або у² = 2рх

— канонічне рівняння параболи, коли  = 1. Парабола симетрична осі Ох, проходить через початок системи координат. Її графік подано на рис. 2.18.

Точка О(0;0) – вершина параболи. Фокус - точка, від якої рівновіддалені сума точок параболи. Ексцентриситет параболи = 1. Дисектриса параболи дорівнює х=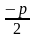

Різновиди парабол: у^2=2px, y^2=-2px, x^2=2py, x^2=-2py

34. Поняття числової послідовності: формула п-го члена, зростаюча спадна, обмежена послідовність.

Розглянемо геометричну інтерпретацію границі послідовності. На числовій осі побудуємо -окіл числа а, тобто інтервал (а – ; а + ), і покажемо, як розміщуватимуться точки, які відповідають членам послідовності , при (рис. 3.12).

Рис. 3.12

Означення. Число а називається границею послідовності x_n, якщо для будь-якого -околу точки а існує номер N такий, що, починаючи з номерів , усі члени послідовності перебувають в -околі точки а (див. рис. 3.12).

Загальні властивості збіжних послідовностей

Теорема 1. (Єдиність границі послідовності). Якщо послідовність має границю, то вона єдина.

Теорема 2. (Необхідна умова збіжності послідовності). Якщо послідовність збіжна, то вона обмежена.

Теорема 3. Якщо , то існує такий но­мер N, що при всіх виконується нерівність .

Теорема 4. Границя сталої величини дорівнює сталій, тобто