25. Різновиди рівняння площини у просторі: за трьома точками, у відрізках на осях, нормальне.

За трьома точками:

Нехай задано три точки М1(x1;y1;z1), M2(x2;y2;z2), M3(x3;y3;z3), а М(x;y;z) – деяка змінна точка площини. Ветори М1М=(x-x1;y-y1;z-z1) М1М2(x2-x1;y2-y1;z2-z1) I M1M3=(x3-x1;y3-y1;z3-z1) лежать у шуканій площині, тобто компланарні, тому мішаний добуток цих векторів дорівнює нулю (М1М*М1М2)*М1М3=0

Перепишемо цю рівність у координатній формі і одержимо рівняння площини за трьома точками:

Нормальне рівняння площини у просторі виводиться аналогічно нормальному рівнянню прямої на площині і має вигляд:

Хсоsa+ycosB+zcosj-p=0, де cosa, cosB, cosj – напрямні косинуси вектора нормалі, р – довжина вектора нормалі,

Рівняння площини у відрізках на осях має вигляд: , де a, b, c – відрізки, які відсікає площина відповідно на осях Ох, Оу, Оz

27. Кут між площинами. Умови паралельності і перпендикулярності двох площин. Відстань від точки до площини

,

.

Двогранний кут  між площинами  і  дорівнюватиме ку- ту між векторами і , перпендикулярними до цих площин (рис. 2.21), тому

. (2.28)

Якщо площини взаємно перпендикулярні, то і, розкривши скалярний добуток у формулі (2.28), дістанемо умову перпендикулярності двох площин:

. (2.29)

Якщо площини  і  паралельні між собою, то їхні вектори і — колінеарні, а отже, відповідні координати пропорційні, і ми маємо умову паралельності двох площин

. (2.30)

За аналогією з формулою знаходження відстані від точки до прямої на площині можна записати формулу знаходження відстані від точки до площини . Вона набирає вигляду

.

29. Кут між прямими в просторі. Кут між прямою і площиною. Умови паралельності і перпендикулярності прямої і площини. Знаходження точки перетину прямої і площини

Кут між двома прямими L1 i L2 визначається кутом фі між напрямними векторами 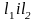цих прямих, а саме:

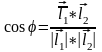
Умови паралельності та перпендикулярності двох прямих у просторі випливають з умов паралельності та перпендикулярності їх напрямних векторів:

Нехай пряма L задана канонічним рівнянням , а площина задана загальним рівнянням Ax+By+Cz+D=0. Нехай - кут між нормальними векторами n=(A,B,C) і напрямним вектором прямої l=(m;k;p). Отримуємо:

- формула кута між прямою і площиною

Умови паралельності і перпендикулярності прямої і площини:

Для відшукання точки перетину прямої і площини Ax+By+Cz+D=0 треба розв`язати систему рівнянь , для чого перейдем від канонічного рівняння прямої до її параметричного рівняння , , z=zo+pt. Підставивши їх у загальне рівняння площини, знайдемо значення параметра t=to. Отримане значення to підставляжмо у параметричне рівняння прямої і знаходимо шукану точку М(хо;уо;zo)

30. Поняття кривих ліній другого порядку. Дослідження рівняння другого порядку. Коло

Кривими лініями 2 порядку називають лінії, координати точок яких задовольняють рівняння другого степеня відносно цих координат.

Колом називається геометричне місце точок площини , рівновідалени від фіксованої точки- центра коло на відстані радіуса кола.

(х-х0)2+(у-у0)2=R2- рівняння кола.

х2+у2=R2-з центром в початку координат.

х2+у2+Ах+Ву+С=0-загальне рівняння.