91.Визначений інтеграл і його властивості

Якщо існує скінченна границя інтегральних сум S_n при _і­­0 і не залежить ні від способу розбиття [a;b] на частини х_і, ні від вибору точок _і, то ця границя називається визначеним інтегралом від ф-ії f(x) на проміжку [a;b] і позначається:

За означенням, визначений інтеграл – число, яке залежить від типу ф-ії f(x) та проміжку [a;b]; він не залежить від того, якою буквою позначена змінна інтегрування.

Ф-ія, для якої на інтервалі існує визначений інтеграл називається інтегровною.

1) Якщо f(x)=c=const, то

2) Сталий множник можна виносити з-під знака визначеного інтеграла.

3) Якщо f₁(x) та f₂(x) інтегровні на [a;b], то:

4) Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл лише змінить свій знак на протилежний.

5) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю.

6) Якщо f(x) – інтегровна в будь-якому із проміжків [a;b], [a;c], [c;b], то:

7) Якщо f(x)0 і інтегровна для x[a,b], b>a, то

8) Якщо f(x), g(x) – інтегровні та f(x)g(x) для x[a;b], b>a, то:

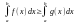
9) Якщо f(x) – інтегровна та mf(x)M, для x[a;b], b>a, то

92.Задача, що призводить до поняття визначеного інтеграла

Обчислити площу криволінійної трапеції аАВв (рис. 7.4).

Розв’язання.

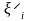Розіб’ємо проміжок [a; b] на n частин точками так що Виберемо точки так: 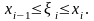Побудуємо прямокутники з основою і висотою (рис. 7.4).

Площа елементарного прямокутника . Площа ступінчастої фігури буде тим менше відрізнятись від площі криволінійної трапеції S_aABb, чим менша довжина , а в граничному випадку ці площі будуть збігатися, тобто

93.Формула Ньютона-Лейбніца для обчислення визначених інтегралів

(Ньютона-Лейбніца): Якщо ф-ія f(x) – неперервна для x [a;b], то визначений інтеграл від ф-ії f(x) на проміжку [a;b] дорівнює приросту первісної ф-ії f(x) на цьому проміжку, тобто:

де F’(x)=f(x)

Зв’язок між визначеним та невизначеним інтегралами можна представити такою рівністю:

Наслідок: Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральної ф-ії і виконати над нею подвійну підстановку.

94.Метод безпосереднього інтегрування визначених інтегралів

95.Метод інтегрування заміни змінної у визначеному інтегралі

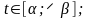Якщо: 1) — неперервна для ; 2)  3) та — неперервні для 4) при то

(7.13)

Зауваження. При заміні змінної інтегрування у визначеному інтегралі змінюються межі інтегрування, і тому нема потреби повертатись до початкової змінної.

Приклад.

=

96.Метод інтегрування частинами у визначеному інтеграла

Теорема 11. Якщо функції та мають неперервні похідні для , то

97.Застосування визначеного інтеграла до обчислення площ фігур, обмежених лініями

98.Невласний інтеграл з нескінченною верхнею межею

99.Невласний інтеграл з нескінченною нижньою межею

Якщо f(x) — інтегровна для скінченних a та b, тобто формули для обчислення невласних інтегралів на нескінченному проміжку мають вигляд:

100.Відмінність між невласними інтегралами І і ІІ роду

101.Невласний інтеграл ІІ роду

Якщо існує скінченна границя , то її називають невласним інтегралом ІІ роду і позначають . Якщо функція f(x) необмежена на [a,b], то їїточки розриву можуть бути на лівому кінці або на правому кінці, або всередині проміжку інтегрування. У цих випадках невласні інтеграли визначаються: , , . Якщо границі існують, то їх і називають невласним інтегралом ІІ роду від функції f(x) на відрізку [a;b]. Якщо границі не існують, або є нескінченними, то невласний інтеграл розбіжний