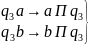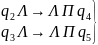10.2. Машини Тьюрінга

Машина Тьюрінга - це математична модель пристрою, який породжує обчислювальні процеси. Використовується для теоретич­ного уточнення поняття алгоритму та його дослідження. Названа за ім'ям англійського математика А.Тьюрінга (A. Turing), який запровадив її 1936 р. У кожній машині Тьюрінга є три частини (рис. 10.1):

1. стрічка, поділена на комірки;

2. пристрій керування (ПК);

3. головка читання / запису (Г).

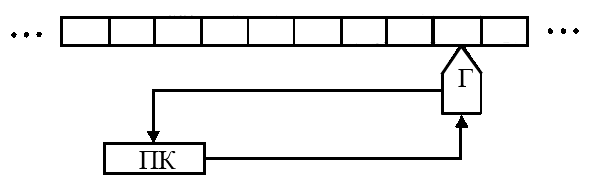
Рис. 10.1

З кожною машиною Тьюрінга пов'язані два скінченні алфавіти: алфавіт зовнішніх символів А і алфавіт внутрішніх станів Q={q₀, q₁, ..., q_k}. З різними машинами Тьюрінга можуть пов'язу­ватись різні алфавіти.

Алфавіт зовнішніх символів А часто називають зовнішнім алфавітом, а його елементи - буквами. Один символ з А називають порожнім, зазвичай його позначають Λ. Всі інші букви з А, крім Λ, називають непорожніми. Комірку стрічки, у якій записано букву А, називають порожньою.

Машина Тьюрінга працює в часі, що вважають дискретним, і його моменти занумеровують 1, 2, З,... .У кожний момент часу стрічка містить скінченну кількість комірок. Головка пересувається поздовж стрічки; у кожний момент часу головка перебуває над певною коміркою стрічки. У такому разі кажуть, що головка зчитує букву, яка записана в цій комірці. У наступний момент часу головка залишається над цією ж коміркою (що позначають H), або пересувається на одну комірку вправо (що позначають П), або пересувається на одну комірку вліво (що позначають Л). Якщо у певний момент t головка перебуває над крайньою коміркою і зсувається на відсутню комірку, то автоматично прибудовується нова порожня (тобто з порожньою буквою Λ) комірка, над якою у момент часу t+1 перебуватиме головка. Отже, стрічка є потенці­ально нескінченною в обидва боки, тобто до неї завжди як зліва, так і справа можуть бути додані нові комірки.

Алфавіт внутрішніх станів Q ={q₀, q₁, ..., q_k} - це внутрішня пам'ять. Внутрішня пам'ять скінченна (на відміну від нескінченної зовнішньої пам’яті на стрічці). Елемент q₀ називають заключним внутрішнім станом, а елемент ^Я початковим внутрішнім станом. Пересування головки поздовж стрічки залежить від букви, яка зчитується, і від внутрішнього стану машини.

Пристрій керування в кожний момент часу t, залежно від букви, яка зчитується у цей момент на стрічці, і внутрішнього стану машини, виконує такі дії:

1. змінює букву а_i , яка зчитується в момент t на стрічці на нову букву а_j (зокрема, може бути a_j=a_i);

2. пересуває головку в одному із напрямів Н, П, Л;

3. змінює наявний у момент t внутрішній стан машини q_i на новий стан щ у якому машина буде в момент часу t+1 (зокрема, може бути q_j=q_i).

Таку дію пристрою керування називають командою, і її записують так:

q_ia_i→a_jDq_j ,

де q_i — внутрішній стан машини в даний момент; а_i - буква на стрічці, яка зчитується в цей момент; а_j - буква, на яку змінюється буква а_i (може бути а_j=а_i); символ D є або Н, або П, або Л і вказує напрямок пересування головки; q_j - внутрішній стан машини у наступний момент часу (може бути q_j=q_i).

Вирази q_ia_i та a_jDq_j називають, відповідно, лівою та правою частинами команди. У лівій частині жодної команди q₀ не зустрі­чається. Всіх команд, у яких ліві частини попарно різні, скінченна кількість (оскільки множини Q\{q₀} та А скінченні), і їх сукуп­ність називають програмою машини. Зазначимо, що жодні дві команди не можуть мати однакові ліві частини.

Виконання однієї команди називають кроком. Обчислення (або робота) машини Тьюрінга - це послідовність кроків одного за другим без пропусків, починаючи з першого. Робота машини Тьюрінга повністю визначена заданням у перший (тобто почат­ковий) момент:

1. слова на стрічці, тобто послідовності букв, записаних у комір­ках стрічки (слово одержують читанням цих символів у комірках стрічки зліва направо);

2. положення головки Г;

3. внутрішнього стану машини.

Сукупність цих трьох умов (у даний момент часу t) називають конфігурацією (у даний момент часу t). Зазвичай у початковий момент внутрішнім станом машини є q₁ а головка перебуває над першою зліва коміркою стрічки.

Отже, у початковий момент конфігурація така: на стрічці, яка складається із деякої кількості комірок (не менше однієї), у кожній комірці записана одна з букв зовнішнього алфавіту А, головка перебуває над першою зліва коміркою стрічки і внутрішнім станом машини є q₁. Наприклад, якщо в початковий момент на стрічці записано слово a₁Λa₂a₁a₁, то початкова конфігурація така:

q1

Λ

a2

a1

a1

q₁

(біля комірки, над якою перебуває головка, вказано внутрішній стан машини).

Отже, програма і початкова конфігурація повністю визначають роботу машини над словом, яке є на стрічці у початковій конфігурації. Тому машину Тьюрінга вважають заданою, якщо відома її програма.

Якщо в роботі машини Тьюрінга в деякий момент t виконається команда, права частина котрої містить q₀, то в такий момент роботу машини вважають завершеною і кажуть, що машина є застосовною до слова на стрічці у початковій конфігурації. Справді, q₁ не зустрі­чається у лівій частині жодної команди, цим і пояснюється назва q₀ - "заключний стан". Результатом роботи машини у такому випад­ку вважають слово, яке буде записане на стрічці в заключній конфі­гурації, тобто в конфігурації з внутрішнім станом q₀.

Якщо ж у роботі машини в жодний момент часу не зустрічається заключний стан, то процес обчислень буде нескінченним. У такому випадку кажуть, що машина є незастосовною до слова на стрічці у початковій конфігурації.

Зазначимо, що q₀∈Q для кожної машини Тьюрінга.

Приклад 10.1. Побудуємо машину Тьюрінга T₁, яка застосовна до всіх слів в алфавіті {a, b} і довільне слово х₁х₂...х_п, де хi∈{а, b}, i=1,..., n, перетворює у слово x₂...х_nх₁.

Як зовнішній алфавіт машини візьмемо множину А={Λ, а, b}, а команди визначимо так:

Команда q1a→ΛПq2 q1b→ΛПq3

Коментар Перша буква а запам'ятовується переходом у стан q2 і стирається. Перша буква b запам'ятовується переходом у стан q3 і стирається. Проходження головки через слово х2...хn і запис у його кінці букви х1=а. Проходження головки через слово х2...хn і запис у його кінці букви х1=b.

Ці команди можна записати у вигляді таблиці, яку називають ункціональною схемою Тьюрінга (табл. 10.1).

Таблиця 10.1

	Λ	a	b
q1	-	ΛП q2	ΛПq3
q2	aНq0	aПq2	bПq2
q3	bНq0	aПq3	bПq3

У таблиці прочерком відзначена неістотна команда, тобто коман­да, яка не зустрінеться під час роботи цієї машини.

Розглянемо роботу машини Т₁ над словом abb; конфігурації, які у цьому разі виникають, зображено на рис. 10.2. ▲

a

b

b

Λ

b

b

q₁ q₂

Λ

b

b

Λ

b

b

Λ

q₂ q₂

Λ

b

b

a

q₀

Рис. 10.2

Приклад 10.2. Побудуємо машину Тьюрінга Т₂ яка є застосов­ною до всіх слів в алфавіті {а,b} і знімає копію слова на стрічці, тобто зі слова х₁...х_п у початковій конфігурації отримаємо слово х₁...х_п Λ х₁...х_п у заключній конфігурації.

Цю машину можна побудувати так. Нехай задано деяке слово в алфавіті {а, b}, що складається з п букв (n≥1). Робота машини буде складатись з n циклів. Для i≤n на початок і-го циклу конфі­гурацію зображено нарис. 10.3.

x1

x2

…

xi-1

xi

xi+1

…

xn

Λ

x1

x2

…

xi-1

q₁

Рис. 10.3

Отже, скопійовано (i-l) букв заданого слова і головка зчитує букву x_i. Черговий цикл здійснюватиметься в три етапи.

Перши етап. Запам'ятовування букви х_i (при цьому вона позна­чається, тобто фактично замінюється іншою буквою) і пересування головки вправо.

Другий етап. Пошук правої крайньої порожньої комірки, в яку записується х_i.

Третій етап. Повернення головки вліво до позначеної букви, стирання позначки (тобто відновлення букви х_i) і пересування головки на одну клітку вправо.

Перший етап реалізують такі команди.

Команда	Коментар
	а' - позначена буква a, q2 - стан запам'ятовування букви а.
q1b→b'Пq3	b' - позначена буква b, q2 - стан запам'ятовування букви b.

Другий етап.

Команда	Коментар
	Проходження залишку слова у стані q2.
	Проходження залишку слова у стані q3.
	Проходження головки через Λ між словами; q4- копіюватиметься буква а; q5 - копіюватиметься буква b.
	Проходження початкової частини копії слова.
	Запис букви, яка копіюється.

Третій етап.

Команда	Коментар
	Рух головки вліво до позначеної бук­ви, стирання позначки, пересування на одну клітку вправо з'переходом у початковий стан q1. Машина готова до виконання чергового циклу копі­ювання букви.
q1Λ→ΛΗq0	Команда зупинки, копію слова побу­довано.

Таблиця 10.2

	Λ	a	b	a'	b'
q1	ΛΗq0	a'Пq2	b'Пq3	-	-
q2	ΛПq4	aПq2	bПq2	-	-
q3	ΛПq5	aПq3	bПq3	-	-
q4	аЛq6	aПq4	bПq4	-
q5	bЛq6	aПq5	bПq5	-	-
q6	ΛЛq6	aЛq6	bЛq6	aПq1	bПq1

Зовнішнім алфавітом машини Т₂ є множина A={Λ, а, b, а', b'}, множина внутрішніх станів Q={q₀, q₁, …, q₆} Нарешті, запишемо команди у вигляді функціональної схеми Тьюрінга (табл. 10.2).

Звернемо увагу, що алфавіт зовнішніх символів А в цьому прикладі окрім порожньої букви Λ та букв аib,у яких записують слово для копіювання, містить ще додаткові букви а', b' які викорис­товують у проміжних обчисленнях. ▲