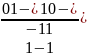8.5.2. Методи побудови скороченої днф

Одним із методів знаходження скороченої ДНФ функції є метод, запропонований 1952 р. Куайном (W. Quine). У цьому методі до досконалої ДНФ булевої функції послідовно застосовують такі рівносильності:

неповне склеювання ;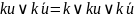

поглинання (члена ки)

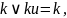
де k-- елементарна кон'юнкція,и - змінна. Кажуть, що члениku та 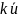склеюються поuі в результаті даютьk. Склеювання назива­ють неповним, оскільки члениku та залишаються у правій частині.

Алгоритм Куайна.

Крок 1.Булеву функцію f(x₁,...,х_n), яку потрібно мінімізувати, записати у досконалій ДНФ, позначити її f₀. Виконати i:=0.

Крок 2.Якщо до ДНФ fне можна застосувати жодного неповного склеювання, то зупинитись:f_i - скорочена ДНФ. Інакше на основі ДНФf_iпобудувати ДНФf_i+1 за таким правилом: у форміf_i. виконати всі неповні склеювання, які можна застосувати до елеме­нтарних кон'юнкцій рангуп-і, після цього вилучити всі елемен­тарні кон'юнкції рангуп-і, до яких можна застосувати поглинання.

Крок 3.Виконати і:=і+1 і перейти до кроку 2. ▲

Отже, в алгоритмі Куайна, починаючи з досконалоїДНФ f₀ будують послідовність ДНФf₀,f₁, f₂,... доти, доки не отримають скоро­чену ДНФ.

Алгоритм Куайна обґрунтовує така теорема.

Теорема 8.26.Для будь-якої булевої функціїf результатом застосування алгоритму Куайна до досконалої ДНФ цієї функції є скорочена ДНФ функціїf.▲

Приклад 8.25.Побудуємо скорочену ДНФ для булевої функції, яку задано досконалою ДНФf₀:

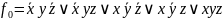
Виконаємо i:=0. Застосовуючи неповне склеювання до членів 1 та 2, 2 та 5, 3 та 4, 4 та 5, одержимо

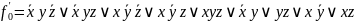
Після п'ятикратного застосування поглинання, одержимо

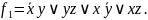
Виконаємо i:=1. Оскільки жодне неповне склеювання не може бути застосоване, то дістали кінцевий результат і f₁ - скорочена ДНФ.▲

Мак-Класкі (МсСluskеу) удосконалив алгоритм Куайна.

Алгоритм Мак-Класкі.

Крок 1.Булеву функцію, яку потрібно мінімізувати, записати у досконалій ДНФ.

Крок 2.Упорядкувати змінні й записати їх у кожній елементар­ній кон'юнкції у вибраному порядку. Після цього зобразити кожну елементарну кон'юнкцію послідовністю з 1, 0 та - (риска). На i-й позиції записати 1, якщо i-а змінна входить до елементарної кон'юнкції без заперечення, 0, якщо входить із запереченням, і риску, якщо зовсім не входить. Наприклад, елементарні кон'юнкціїхуz, 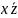, 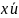записують, відповідно, у вигляді 111-, 1-0-, 1- - 0.

К

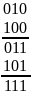
рок 3.Розбити двійкові вирази, які відповідають елементарним кон'юнкціям, на класи за кількістю одиниць, і розташувати списки цих класів у порядку зростання кількості одиниць. Для досконалої ДНФ із прикладу8.25отримаємо список із п'яти елементів, розбитих на три класи.

Крок 4.Виконати всі можливі склеювання 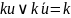. Склею­вання можна застосувати лише до елементів списку, які містяться у сусідніх класах. Елементи, які склеюють, знаходять у сусідніх класах простим порівнянням: ці елементи повинні відрізнятись точно в одній позиції і в цій позиції не повинна бути риска (-).

Якщо помістити до одного класу всі k, які були отримані із двох сусідніх класів, то на наступному кроці знову доведеться порів­нювати лише елементи із сусідніх класів. Елементи, які беруть участь у склеюванні, позначити *; надалі вони не залишаться у списку простих імплікант. Попередній список після опрацювання матиме такий вигляд:

Непозначеними * залишилися 4 елементи: 01-; 10-; -11; 1-1. Отже, множина всіх простих імплікант функції

така:

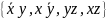а її скорочена ДНФ- . ▲

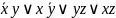МетодБлейка. В алгоритмах Куайна і Мак-Класкі знаходження скороченої ДНФ починають з досконалої ДНФ. У багатьох випад­ках доводиться знаходити скорочену ДНФ функції, що задана довільною ДНФ (не досконалою ДНФ). У таких випадках доцільно користуватись методом Блейка (A. Blake).

Метод Блейка заснований на застосуванні рівносильності уза­гальненого склеювання.

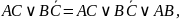
де А,В,С- довільні формули.

Якщо, у цій рівносильності АВ≠0, то кажуть, що до членівАСта ВСможна застосувати нетривіальне узагальнене склеювання.

Доведемо рівносильність узагальненого склеювання, викори­стовуючи закони алгебри Буля:

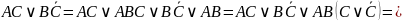
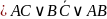
Теорема 8.27.Якщо в будь-якій ДНФ булевої функціїfвиконати всі можливі узагальнені склеювання і після цього всі поглинання, то в результаті одержимо скорочену ДНФ функціїf.

Доведення. ґрунтується на тому, що в результаті багатократного застосування рівносильності узагальненого склеювання до довіль­ної ДНФ булевої функції можна отримати будь-яку просту імпліканту цієї функції. ▲

Метод Блейка полягає в тому, що у довільній ДНФ заданої булевої функції спочатку здійснюють усі допустимі узагальнені склеювання(причому отримані в результаті узагальнених склеювань члени беруть участь у нових узагальнених склеюваннях). Після цього здійснюють поглинання, тобто вилучають диз'юнктивні члени вигляду АВ у разі наявності диз'юнктивних членів А або В. У результаті отримують скорочену ДНФ.

Приклад 8.26. Знайдемо за методом Блейка скорочену ДНФ булевої функції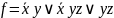 . Легко побачити, що перший і другий члени формули fдопускають узагальнені склеювання як по jc, так і по>>. Але члени, які виникають у результаті цих склеювань, дорівнюють нулю. Нетривіальне узагальнене склеювання тут мож­ливе лише для першого і третього членів формули f. Застосуємо це склеювання й одержимо ДНФ .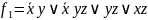

У цій формі нетривіальне узагальнене склеювання можна застосувати до першого і третього, а також до другого і четвертого членів. Проте, обидва ці склеювання дають члени, які вже є у формі f₁. Отже, можна вважати, що у формі f₁виконані всі можливі в ній узагальнені склеювання. Виконаємо поглинання (член 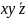поглинається членомyz)і одержимо скорочену ДНФ ▲

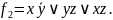Розглянемо, ще один метод побудови скороченої ДНФ - метод Нельсона (R. Nelson).Цим методом зручно користуватись, якщо функція задана довільною кон'юнктивною нормальною формою.

Метод Нельсона обґрунтовує така теорема.

Теорема 8.28. Якщо в будь-якій кон'юнкгивній нормальній формі булевої функції розкрити всі дужки відповідно до дистрибутивного закону і виконати всі поглинання, то в результаті отримаємо скорочену ДНФ цієї функції.

Для доведення достатньо переконатись, що у разі розкриття дужок удовільній кон'юнктивній нормальній формі d_l∧d₂∧...∧d_mбулевої функції fможна отримати будь-яку наперед задану просту імплікантуkцієї функції.▲

Приклад 8.27. Розглянемо булеву функціюf, задану кон'юн­ктивною нормальною формою .

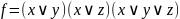Розкриваючи дужки: .

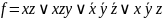Виконаємо поглинання й одержимо скорочену ДНФ булевої функціїf:

.▲

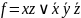Методи Куайна, Мак-Класкі, Блейка, Нельсона використовують для знаходження скороченої ДНФ, що складає перший етап міні­мізації.