3.3. Методы вычисления

ПАРАМЕТРИЧЕСКИХ ОПИСАНИЙ

ГРАНИЦ ОБЛАСТЕЙ

Описание геометрических свойств области с помощью топо­логических и метрических признаков часто бывает недоста­точным в том смысле, что объекты с существенно разными по форме границами областей характеризуются приблизительно одинаковыми значениями рассмотренных выше метрических признаков. Эту ситуацию иллюстрирует рис. 3.4, на котором показаны три объекта (XB₁, XB₂, XB₃), имеющие существенно разную форму границ и достаточно близкие значения приз­наков размера, формы, местоположения и ориентации. Други­ми словами, ситуация на рис. 3.4 свидетельствует о недостаточности метрических и топологических признаков для построения описаний нужного уровня информативности и необходимости перехода к так называемым параметрическим описани­ям границ областей. Проанализируем методы и алгоритмы вычисления таких описаний.

Для получения параметрических описаний границ используются три основных методических направления: цепное кодирование, функциональные параметрические описания, аппроксимационные описания границ.

Цепное кодирование является широко известным способом описания границы дискретного объекта. Цепным кодом Сс (кодом Фримэна) называют последовательность целых чисел от 0 до 7, задающих одно из семи дискретных направлений при переходе от одной граничной точки к следующей при выбранном направлении обхода границы (рис. 3.5). Граница при этом понимается как замкнутая цепочка в смысле вось­ми соседей. В случае, когда границу объекта понимают как замкнутую цепочку в смысле четырех соседей, для ее кодиро­вания может использоваться так называемый «разрывный» цепной код Rc (см. рис. 3.5,б) [10]. Фактически цепной код Сс определяет угол как функцию длины дуги с учетом того, что диагональные отрезки в раз длиннее, чем вертикальные или горизонтальные. В этом смысле цепной код для замкну­тых кривых (цепочек) представляет собой периодическую функцию с периодом NP. В зависимости от выбора начальной точки отсчета одна и та же кривая кодируется, вообще го­воря, разными цепными кодами. Вот почему часто рассматри­вают нормализованный код, однозначно описывающий ту или иную дискретную цепочку. Нормализованный цепной код явля­ется таким, который минимизирует целое восьмеричное число, представляемое последовательностью цифр от 0 до 7. Для до­стижения инвариантности цепного кодирования по отношению к параметрической группе преобразований плоскости (парал­лельный перенос, вращение, изменение масштаба) рассматривают «производную» цепную кода — Сс'. «Производная» цеп­ного кода есть число поворотов против часовой стрелки, ко­торое нужно сделать от направления в одной точке до достижения направления в следующей точке, взятое по модулю 8. На рис. 3.6 показана инвариантность кода Сс' к вращению некоторой дискретной фигуры.

Цепное кодирование границ дискретных объектов облада­ет рядом полезных свойств. Цепной код можно рассматривать как эффективный для сжатия информации код по сравнению с покоординатным методом запоминания границы. Представление границы объекта в виде цепного кода дает доста­точно простые алгоритмы определения его площади NS и пе­риметра NP. Наконец, цепное кодирование обеспечивает возможность сравнивать форму двух дискретных кривых [17]. Для этой цели можно использовать цепную взаимнокорреляционную функцию

,

где DP = {dp₁, dp₂, ..., dp_n}, DQ={dq₁, dq₂, ..., dq_n} - дис­кретные цепочки на дискретной решетке DG'; n — длина цепо­чек; — косинус разности углов, соответствующих эле­ментам dp_i и dq_i.

Благодаря названным полезным свойствам и простым вы­числительным алгоритмам метод цепного кодирования для па­раметрического описания границ получил широкое распространение.

Функциональные параметрические описания используют для представления границ объектов следующие функциональные зависимости:

,

, (3.6)

,

,

где — относительное изменение расстояния от центра тяжести фигуры до граничной точки в зависимости от уг­ла поворота радиуса-вектора  и длины дуги s; — изменение угла поворота радиуса вектора r в зависимости от длины дуги s; – изменение угла наклона касательной () к оси абсцисс в зависимости от длины дуги s; — спектр Фурье от функции кривизны кривой k(s).

Первые две зависимости называют также контурами Фримэна, а третью зависимость — «пси-эс» кривой. На рис. 3.7 эти зависимости показаны для окружности и фигуры с более «сложной» формой границы. Регулярная форма границы круга делает значения _r, _,  малоинформативными (см. рис. 3.7а); в то же время усложнение формы границы приводит к появле­нию определенных закономерностей функциональных кривых. Так, горизонтальные, приблизительно постоянные участки «пси-эс» кривой соответствуют пологим, гладким участкам границы объекта (участки с малой кривизной), а «скачки», резкие переходы — углу на границе либо точке перегиба. Кривая _r(s) строится так, что в качестве точки отсчета (нулевого значения ) всегда берется положение максимального по длине радиус-вектора r_max, принимаемого за ось отсчета.

На рис. 3.8 показаны контуры Фримэна для прямоуголь­ника, звезды и кленового листа. При этом верхний график соответствует функции _(s), а нижний — функции _r(s). Длины графиков соответствуют числу точек дискретизации границы описываемой фигуры. Эта дискретизация границ задает шаг по аргументам s и .

Здесь можно выявить также ряд закономерностей изме­нения формы границы и соответствующие изменения форм кривых _r, _. Кривая _r, характеризуя относительную удален­ность граничной точки фигуры от центра тяжести, имеет не­монотонный характер, так что впадины кривой соответствуют вогнутостям (заливам) фигуры, а максимумы выпуклостям (полуостровам). Чем регулярнее форма фигуры, тем регулярнее кривая _r (см. рис. 3.8,а). В отличие от кривой _r кривая _ носит монотонный характер для большинства форм границ. Производная d_ (s)/ds непостоянна и больше там, где присутствуют впадины у _r и вогнутости у границы; малые значения производной d_(s)/ds соответствуют участкам выпуклостей формы фигуры. Нарушение монотонности кривой _ может произойти, когда форма фигуры будет допускать «обратный ход» луча, что имеет место, например, для слож­ных спиралевидных форм.

На рис. 3.9 показаны контуры Фримэна реальных хромосом. По-прежнему верхний график является кривой_(s), a нижний — кривой _r(s). Обращает на себя внимание ситуация на рис. 3.9,в, где иллюстрируемый объект представляет собой две хромосомы, наложенные друг на друга. Огибающая дан­ную фигуру внешняя граница дает пример такой формы, когда нарушается монотонность кривой _(s).

Спектр S_FR() обеспечивает информацию о пространственных частотах «наполняющих», как правило, полигармонический сигнал k(s). Можно ожидать, что этот спектр будет очень «беден» для границы объекта ХВ₁ (см. рис. 3.4), содержать небольшое число низкочастотных коэффициентов для границы объекта ХВ₂ и иметь значительную по интенсивности высоко­частотную составляющую для границы объекта ХВ₃. Таким образом, чем сильнее изрезанность формы границы, тем «богаче» состав пространственных частот в спектре S_FR(). Этот метод является достаточно точным, если использовать большое (несколько десятков или сотен) число спектральных коэф­фициентов, а также дает описания, инвариантные к размеру, переносу и вращению фигур [32, 41, 47].

Алгоритмическая реализация обсуждаемых методов приводит к разным по вычислительной сложности алгоритмам. Наиболее просто осуществляется подсчет функциональных зави­симостей _r(s) = f₁(s), _(s) = f₂(s). Здесь достаточно, прослеживая граничные точки дискретного объекта, подсчитывать расстояние между последними и центром тяжести — точкой с коорди­натами (i₀, j₀) либо угол между осью отсчета и текущим по­ложением радиус-вектора. Подсчет зависимости = f₃(s) тре­бует привлечения алгоритмов нахождения приращения угла поворота радиус-вектораrи угла наклона касательной к граничной точке.

В основе этих алгоритмов могут лежать вычислительные соотношения для определения главных направлений участков граничной кривой, центрированных в анализируемых точках на границе объекта [14]. В случае, когда размеры дискретных объектов велики (величина NP достигает значений 100 и более), для подсчета функциональных зависимостей (3.6) можно использовать «прореживание» граничных точек, выбирая для анализа, например, каждую вторую, третью и т. д. точки. Этот процесс соответствует выбору нужного шага квантования ар­гументов s и .

Алгоритмическая реализация Фурье-дескриптора S_FR() имеет ряд особенностей [17, 32]. Несмотря на то, что дис­кретный вариант функции k(s) можно подсчитать по соотношению, приведенному в приложении, эта функция неудобна для использования в нескольких отношениях. Для прямоуголь­ника, например, эта функция тождественно равна нулю всю­ду, кроме четырех точек (вершин), где она принимает бесконечные значения, функция k(s) не определена также в точках, где граница резко меняет направление (угловые точки). Дискретный вариант этой функции k_m(c_i), i = 1, ..., NP зависит от параметра т, оптимальное значение которого необходимо подбирать эмпирически. Вот почему вычисление S_FR() реко­мендуется осуществлять не для функции k(s), а для «пси-эс» кривой, являющейся параметрическим выражением формы границы. При этом нужно учитывать, что часто для примене­ния алгоритма БПФ количество точек у «пси-эс» кривой долж­но быть степенью числа 2 [14]. В [47] предлагается вычислять спектр Фурье от комплексной последовательности , представляющей собой декарто­вы координаты граничных точек дискретного объекта. Отмеча­ется, однако, что в этом случае возникают серьезные погрешности, связанные с эффектом дискретизации кривой.

Аппроксимационные описания дают аппрок­симацию произвольной границы с помощью аналитической кривой с заданными свойствами непрерывности, гладкости и т. п. В качестве таких кривых, как правило, используют полиномы различных порядков (прямую, параболу, кубический полином). Точность аппроксимации оценивается некоторым чи­словым критерием в зависимости от используемого метода (метода наименьших квадратов, подбора линии по собственному вектору, метода В-сплайнов). Общая математическая по­становка задачи построения аппроксимационного описания имеет следующий вид [14, 17]. Пусть граница области задана упорядоченным набором n точек с декартовыми координатами ^.

Пусть аппроксимирующий полином имеет порядок t и опре­деляется выражением

. (3.7)

Пусть числовой критерии точности (качества) аппроксимации представляет собой функционал

. (3.8)

Необходимо найти значения параметров c₀, c₁, ..., c_t при за­данных {х_i, у_i}, i = l, 2, ..., п, доставляющие экстремальное значение функционалу (3.8). На практике наиболее распространены линейные и кусочно-линейные аппроксимации гра­ниц. В этом случае аппроксимирующий полином (3.7) превращается в аппроксимирующую прямую

.

Если используется метод наименьших квадратов, то критерий точности аппроксимации (3.7) принимает вид

. (3.9)

При сформулированных выше исходных данных задача допускает достаточно простое аналитическое решение [17]. Вводят­ся в рассмотрение следующие матрицы и векторы

.

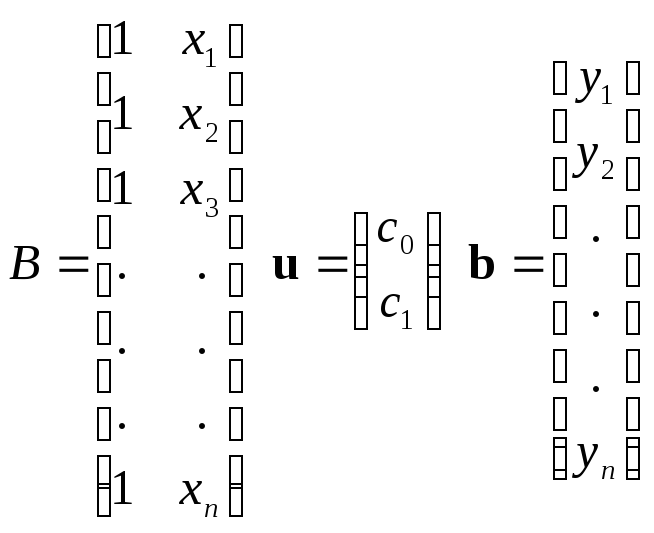Величина в точности равна критерию (3.9) и достигает минимального значения, если . При этом– так называемая псевдообратная матрица. Выполнив несложные вычисления, можно получить

,

, (3.10)

где .

В ряде случаев критерий вида (3.9) неоптимальный, так как его значение зависит от выбранной системы координат и ориентации аппроксимируемой границы в этой системе коорди­нат. Вот почему часто предпочтение отдают методу подбора прямой по собственному вектору [17]. Здесь в качестве крите­рия точности аппроксимации выступает сумма квадратов рас­стояний от граничных точек (х_i, y_i) до прямой. Известно, что этот критерий минимизируется прямой, проходящей через «центр тяжести» множества { х_i, y_i}, i = 1, ..., n, т.е. через, точку с координатами , и параллельно главному собственному вектору матрицы рассеяния этого множества.

Выше рассмотрены описания геометрических структур изображений с помощью признаков трех категорий: топологических, метрических и параметрических. Необходимо отметить что информативность получаемых здесь описаний возрастает при переходе от топологических признаков к метрическим и от метрических признаков к параметрическим описаниям границ.

В основе вычислений метрических признаков лежат фундаментальные понятия и определения дискретной геометрии, а также ряд аппроксимационных формул, приведенных в табл. 3.2. Часть этих признаков может быть вычислена непосредственно путем анализа поля изображения (признаки NS, NP, а, b, i₀, j₀), в то время как другие признаки являются функциями от первых либо вычисляются через вспомогательные параметры (моменты, собственные числа матрицы рассея­ния и т. д.).

Описание границы цепным кодом (кодом Фримэна) удобно для эффективного в смысле затрат памяти запоминания гра­ницы дискретного объекта, а также для вычисления площади и периметра объекта и выполнения операции сравнения формы границ [17]. Функциональные параметрические описания да­ют в конечном счете числовые векторы, отражающие форму границы объекта. Эти векторы могут быть в дальнейшем использованы для определения сходства формы границ либо введением метрики в получающемся векторном пространстве, либо введением другой функции сходства. Аппроксимационные описания границ полезны для отображения формы границы средствами интерактивной машинной графики.