Алгоритм оценки кривизны дискретной кривой через кусочно-линейную аппроксимацию кривой

begin

(* расширение кривой *)

for j := 1 to 2m do

begin x_j+N := x_j; y_j+N := y_j end;

(* подсчет кривизны *)

for i := 1 to N do

Найти кривизну k_i в точке (x_i, y_i) по формуле

end

При этом в алгоритме приняты следующие обозначения:

т — порядок кривизны;

N — число граничных точек дискретной кривой;

А_i — длина отрезка между точками (x_i, y_i) и (x_i-m, y_i-m);

B_i — длина отрезка между точками (x_i, y_i) и (x_i+m, y_i+m);

С_i— длина отрезка между точками (x_i-m, y_i-m) и (x_i+m, y_i+m);

k_i — значение кривизны порядка т в точке (x_i, y_i).

В [31] предложен болей точный способ определения кри­визны, основанный на использовании матриц рассеяния под­множеств точек дискретной кривой. Пусть DC=={c₁, c₂, ..., c_N} — дискретная кривая; т = 2п + 1; т, n - целые числа. Кривизной кривой DC порядка т в точке называют вели­чину

,

где ,— соседние точки кривой; — евклидово расстояние между ними; DC⁽¹⁾ и DC⁽²⁾ — участки кривой DC длиной в m точек с центрами в точках ,, — угол между главными направлениями DC⁽¹⁾ и DC⁽²⁾, задаваемыми собственными векторами матриц рассеяния DC⁽ⁱ⁾, i = 1, 2, которые соответствуют максимальным собствен­ным числам (см. рис. 3.10,6).

Для выделения точек контура, соответствующих вершинам углов на кривой, последовательность значений кривизны, по­лученную в результате работы алгоритма вышеприведенного типа, обычно подвергают двухшаговой обработке:

полученные значения кривизны сравнивают с некоторым пороговым значением;

оставшиеся точки проходят проверку на выполнение усло­вия, являются ли соответствующие им значения кривизны ло­кальными максимумами на достаточно большом подмножестве точек контура.

Наличие проверочной стадии связано с эффектом сглажи­вания, степень которого зависит от величины т при вычисле­нии значений кривизны.

Существуют альтернативные методы отыскания вершин (углов) на дискретной кривой. Один из них основан на вычислении величин отклонений касательной к замкнутой дискрет­ной кривой. При вычислении угла относительного отклонения касательной используют нормализованную матрицу рассеяния множества точек кривой

,

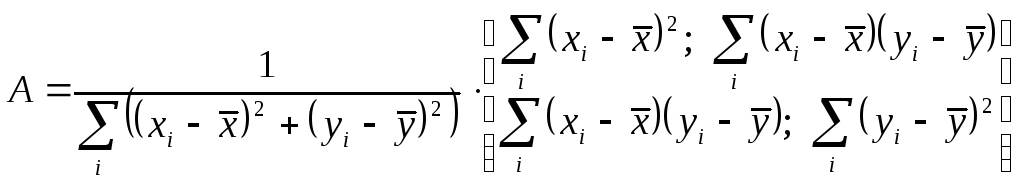где и— соответственно средние значения по координа­там x и у, а сама касательная к кривой в точке понимается как главное направление дискретной дуги с центром в данной точке, задаваемое собственным вектором матрицы рассеяния точек дуги; вектор соответствует максимальному собственному числу.

Пусть дискретная замкнутая кривая задана упорядоченным набором точек с декартовыми координатами: {(x_i, y_i), i = 1, ..., N}. Входными параметрами алгоритма, вычисляющего ко­ординаты «угловых» точек кривой, являются:

порог отклонения касательной , задаваемый в пределах 525° [15];

число точек m, используемых в вычислении матрицы рас­сеяния (аналог порядка кривизны дискретной кривой); обыч­но 515; фактически величинат отражает степень сглаживания кривой: большие значения т приводят к устранению ложных вершин в «зашумленных» данных, но одновре­менно могут способствовать удалению малых по глубине впа­дин и коротких пиков на кривых высокого качества;

 параметр приемлемости условной оси отсчета обычно выбирают в пределах 0,7< <0,9; параметр  характеризует «прямолинейность» выбранной оси, от которой ведется от­счет отклонений касательной;

минимальное число d точек данных между последовательными точками по условной оси отсчета.

Выходными параметрами алгоритма служат идентификато­ры вершин исходной кривой и помеченные в зависимости от способа их определения (либо с помощью сравнения с порогом отклонения касательной , либо в результате превышения параметраd), а также количество вершин с.