Нелинейная регрессия

Зависимость объема производства y (тыс. ед) от численности занятых x (чел.) некоторой фирмы приводятся в таблице.

x	10	12	15	17	21	23
y	29	31	37	39	43	58

Для характеристики зависимости y от x рассчитайте параметры показательной функции у= а*b^x

Построению уравнения показательной кривой у= а*b^x предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения

lgy=lga+x *lgb

Обозначив Y= lg y, А= lg а, В = lg b,

получим: Y=А+B* x

x	y	Y	xY	Y2	х2	Y(х)	y-Y(x)	(y-Y(x))2	А
10,00	29,00	3,37	33,67	11,34	100,00	3,349005	0,02	0,000335	0,005432
12,00	31,00	3,43	41,21	11,79	144,00	3,44392	-0,01	0,0001	-0,00289
15,00	37,00	3,61	54,16	13,04	225,00	3,586291	0,02	0,000606	0,00682
17,00	39,00	3,66	62,28	13,42	289,00	3,681206	-0,02	0,000311	-0,00482
21,00	43,00	3,76	78,99	14,15	441,00	3,871035	-0,11	0,012064	-0,0292
23,00	58,00	4,06	93,39	16,49	529,00	3,965949	0,09	0,008929	0,023272
98,00	237,00	21,90	363,70	80,23	1728,00	21,90		0,022344
16,33	39,50	3,65	60,62	13,37	288,00	3,649568		0,003724

Значения параметров регрессии А и В составили

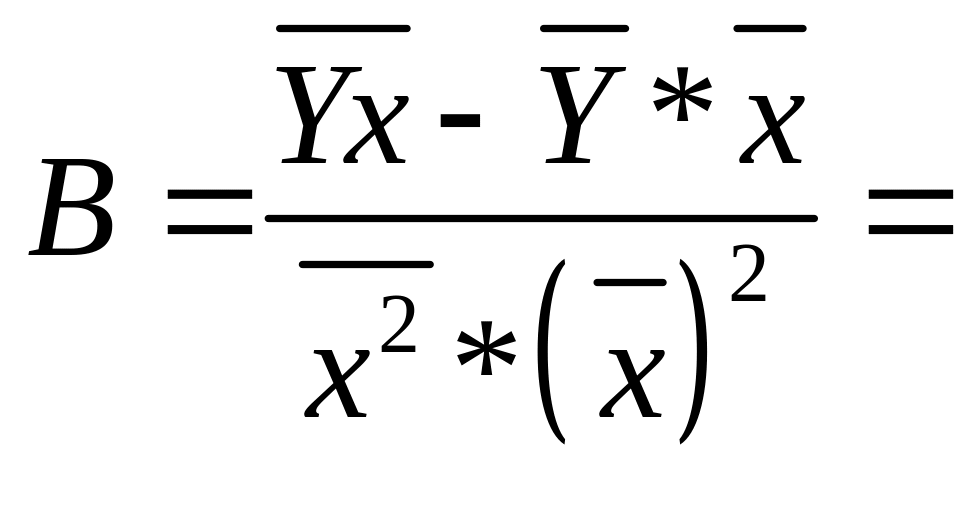0.05

2.874433

Получено линейное уравнение:

Y(x)=2.874433+0.05x

Произведем потенцирование полученного уравнения и запишем его в обычной форме:

Y(x)=10^2.874433*10^0.05x=749*10^0.05x

σ_x= 4.6

σ_y= 0.23

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции r_xy, который можно рассчитать по следующей формуле:

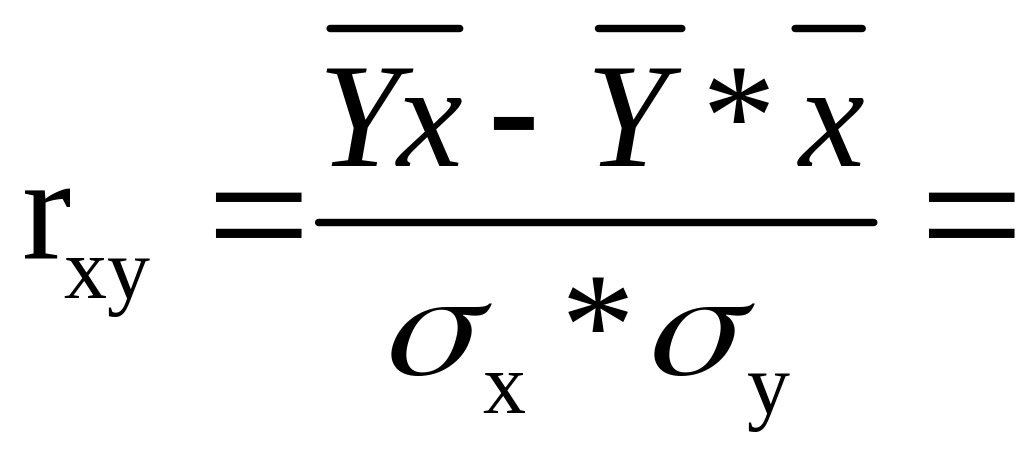0,963

Линейный коэффициент корреляции находится в пределах .Чем ближе абсолютное значение r_xy к единице, тем сильнее линейная связь между факторами (при r_xy = ±1 имеем строгую функциональную зависимость). Но следует иметь в виду, что близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции r²_xy называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака y , объясняемую регрессией, в общей дисперсии результативного признака.

r²_xy=0,927719

Чтобы иметь общее суждение о качестве модели из относительных

отклонений по каждому наблюдению, определяют среднюю ошибку

аппроксимации:

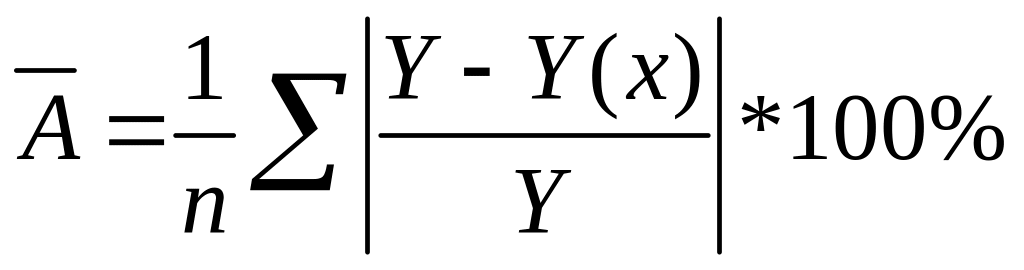=1,2%

Средняя ошибка аппроксимации не должна превышать 8–10%.

Средний коэффициент эластичности:

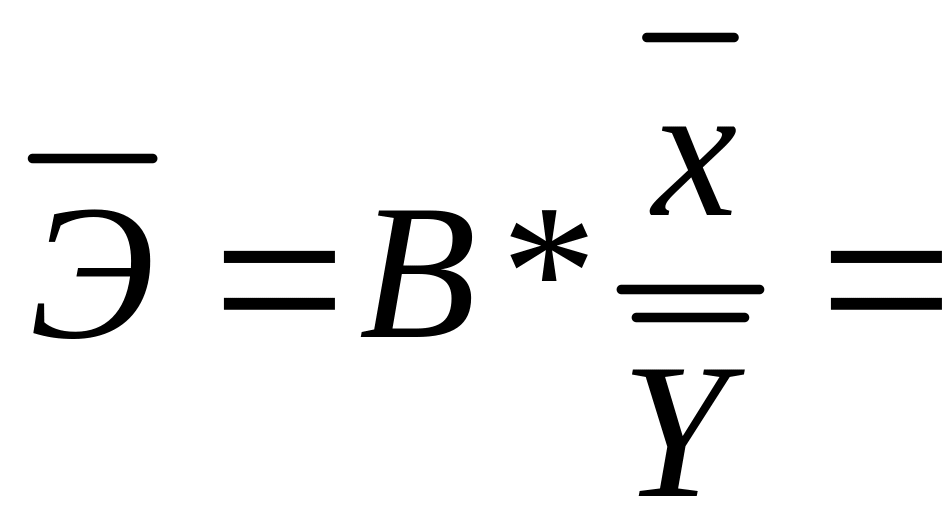12,864

Оценка значимости уравнения регрессии в целом производится на основе F -критерия Фишера, которому предшествует дисперсионный анализ.

В математической статистике дисперсионный анализ рассматривается как

самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.

F-критерий Фишера:

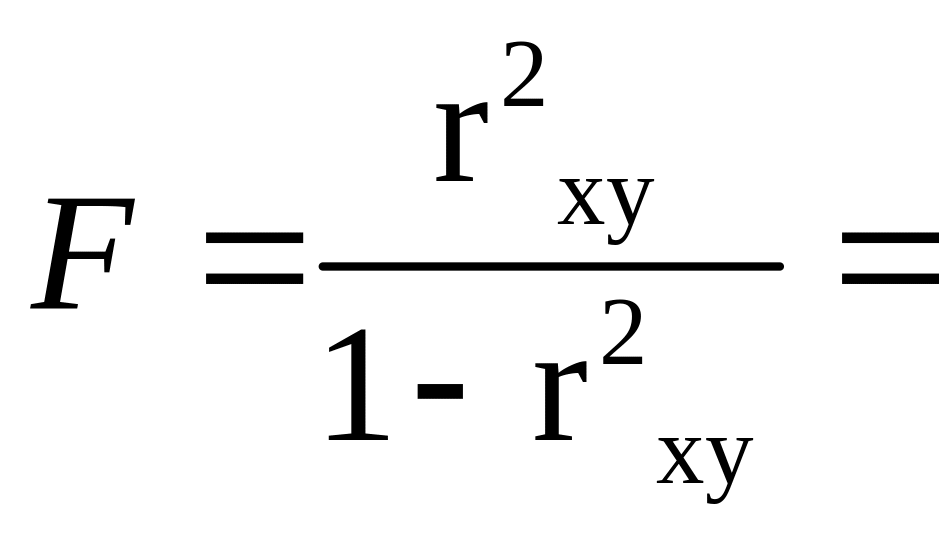51,339

Фактическое значение F -критерия Фишера сравнивается с табличным значением F_табл ( α ;k1;k2 ) при уровне значимости α и степенях cвободы k1=m и k2= n-m-1. При этом, если фактическое значение F -критерия больше табличного, то признается статистическая значимость уравнения в целом. Для парной линейной регрессии m=1, следовательно k1=1, k2=4 и F_табл=7,71.

В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: m_b и m_a.

Стандартная ошибка коэффициента регрессии определяется по

формуле:

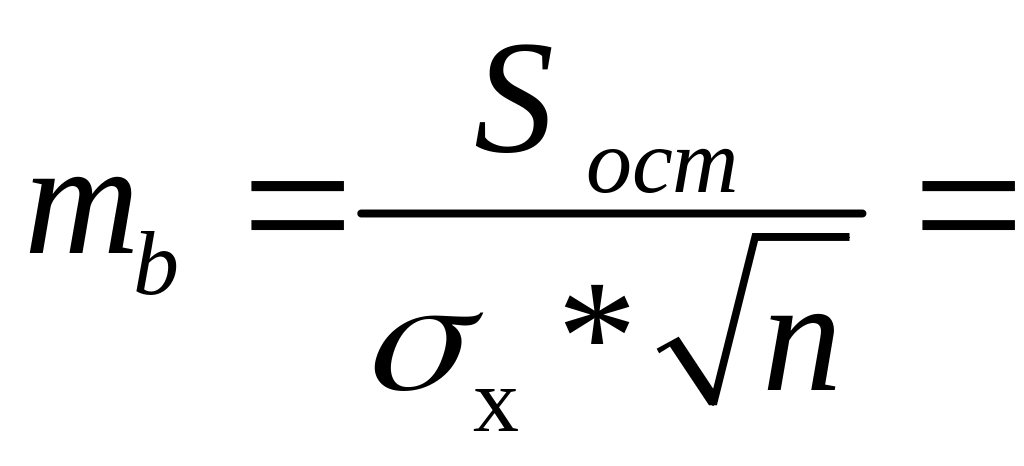0,006623, где 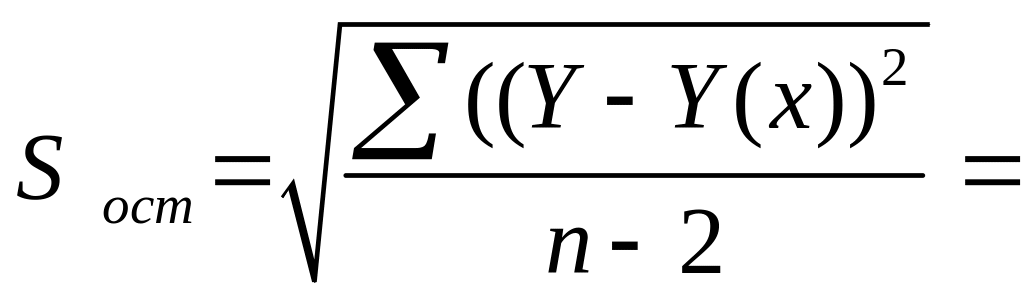0,00558

Величина стандартной ошибки совместно с t –распределение Стьюдента при n −2 степенях свободы применяется для проверки существенности коэффициента регрессии. Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t -критерия Стьюдента 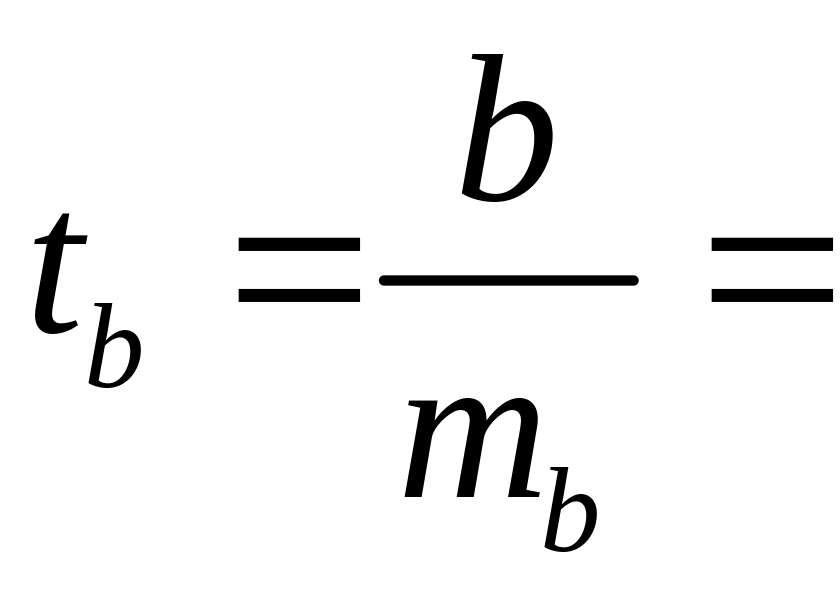7,165, которое затем сравнивается с табличным значением при определенном уровне значимости α и числе степеней свободы (n-2).

Стандартная ошибка параметра a определяется по формуле:

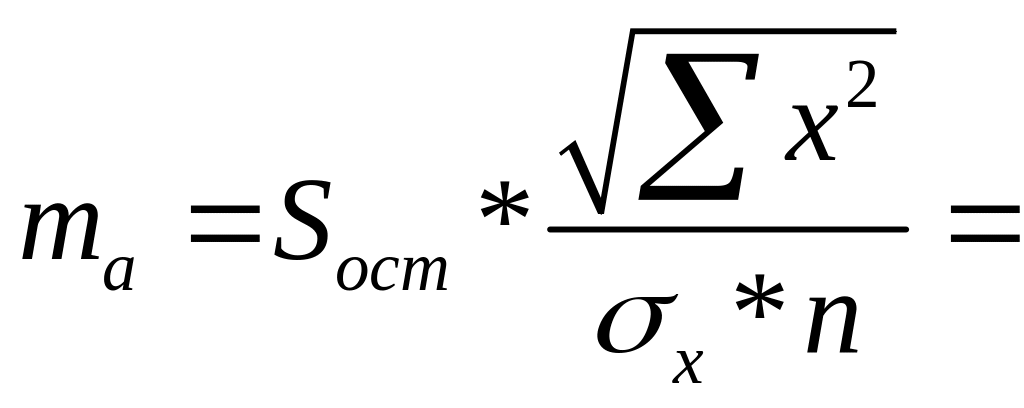0,112

Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется t –критерий 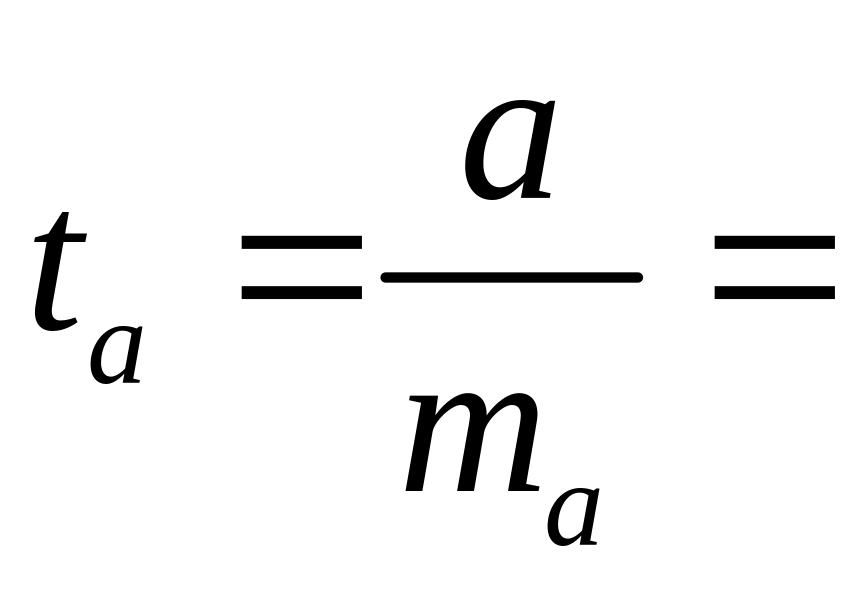25,572.

Значимость линейного коэффициента корреляции проверяется на

основе величины ошибки коэффициента корреляции m_r:

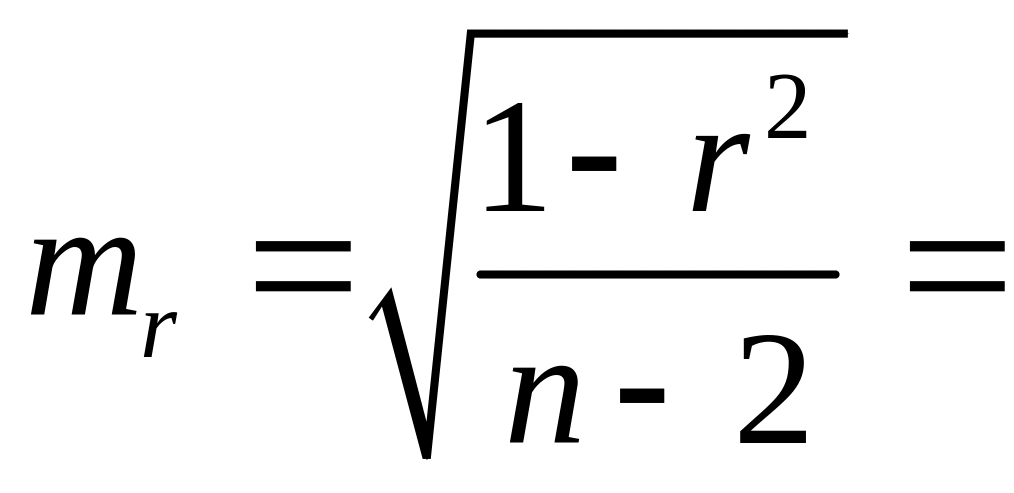0,1344

Фактическое значение t -критерия Стьюдента определяется как 7,2

Табличное значение t-критерия Стьюдента при α=0,05 и числе степеней V=n-2=4, есть 2,7764.

Т.к.t_b>t_табл., t_a>t_табл.,t_r>t_табл., то признаем статистическую значимость параметров регрессии и показателя тесноты связи.

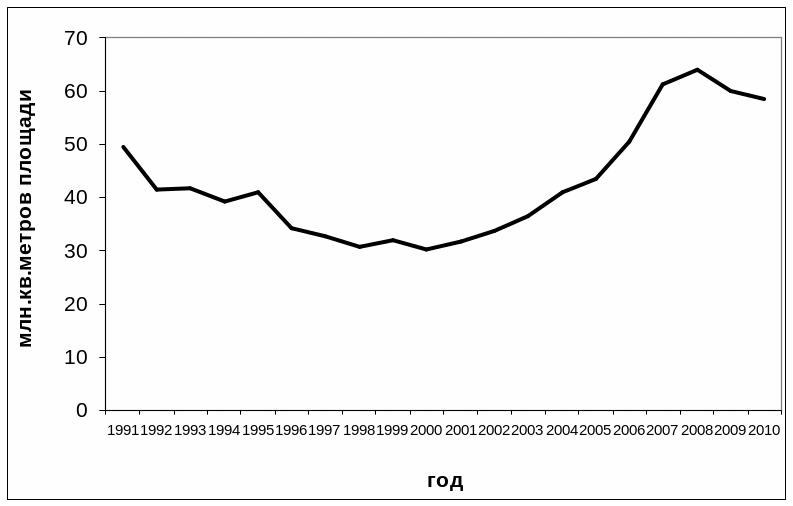
Исследуемые данные и их график

Ввод в действие жилых домов в Российской Федерации

(млн.кв.м общей площади)

Годы	Всего построено
1991	49,4
1992	41,5
1993	41,8
1994	39,2
1995	41,0
1996	34,3
1997	32,7
1998	30,7
1999	32,0
2000	30,3
2001	31,7
2002	33,8
2003	36,4
2004	41,0
2005	43,6
2006	50,6
2007	61,2
2008	64,1
2009	59,9
2010	58,4