Введение
Данная работа посвящена анализу и прогнозированию количества квадратных метров введенной в действие жилой площади в Российской Федерации.
Государственная политика в сфере строительства, содержания и реконструкции жилья рассматривается в контексте антикризисных мер, принятых правительством Российской федерации на среднесрочную перспективу. Общая площадь жилищного фонда Российской Федерации составляет около 3,17 млрд кв. м.Наиболее интенсивный рост его объема пришелся на 70-80-е годы прошлого века, когда ежегодно в эксплуатацию вводилось 59-76 млн кв. м общей площади жилья. Только за последние 10 лет существования СССР жилищный фонд России увеличился почти в 1,5 раза. С 1992 г. ввод жилья стал быстро сокращаться и в течение 12 лет варьировался в пределах 30-41 млн кв. м в год. Восстановление объемов строительства началось лишь в 2005 г., однако пока они существенно ниже «пиковых» показателей советского периода. За десятилетие 2000-2009 гг. жилищный фонд страны вырос всего на 14,8%.
Уровень обеспеченности жильем в России достаточно скромен. К началу 2010 г. в среднем на 1 человека в РФ приходилось примерно 22,3 кв. м жилья, что в 2-3 раза ниже аналогичного показателя в развитых странах. Так, в США обеспеченность жильем составляет около 75 кв. м/чел., в Великобритании – 62 кв. м, Германии – 45 кв. м.
В связи с падением объемов жилищного строительства, к середине 90-х годов рост показателя жилищной обеспеченности стал замедляться, несмотря на сокращение численности населения страны. Так, в 1980-1994 гг. обеспеченность жильем повысилась почти на 6 кв. м на человека при росте населения на 10 млн чел. Уровень строительной активности в первом десятилетии текущего века колебался в РФ в пределах ХХ кв. м/чел. в год.В то же время опыт зарубежных стран показывает, что для кардинального улучшения жилищной обеспеченности в приемлемые сроки (на протяжении жизненного цикла одного поколения), строительная активность должна составлять около 1 кв. м/чел. в год.
Кластерный анализ
По данным, представленным в таблице, провести классификацию n = 4 предприятий по двум показателям
Номер предприятия |
1 |
2 |
3 |
4 |
(1) хi |
9 |
6 |
2 |
8 |
(2) хi |
6 |
10 |
4 |
9 |
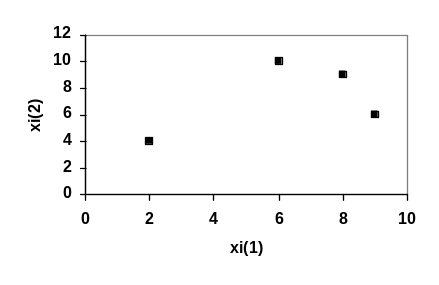
1.Классификация на основе обычного евклидова расстояния принцип “ближайшего соседа”.
ρ
(1,2)=
=5
ρ (2,1)= =5
ρ
(2,3)=
=7,21
ρ (3,2)= =7,21
ρ
(1,3)=
=7,28
ρ (3,1)= =7,28
ρ
(1,4)=
=3,16
ρ (4,1)= =3,16
ρ
(2,4)=
=2,24
ρ (4,2)= =2,24
ρ
(3,4)=
=7,81
ρ (4,3)= =7,81
Построим матрицу расстояний R1
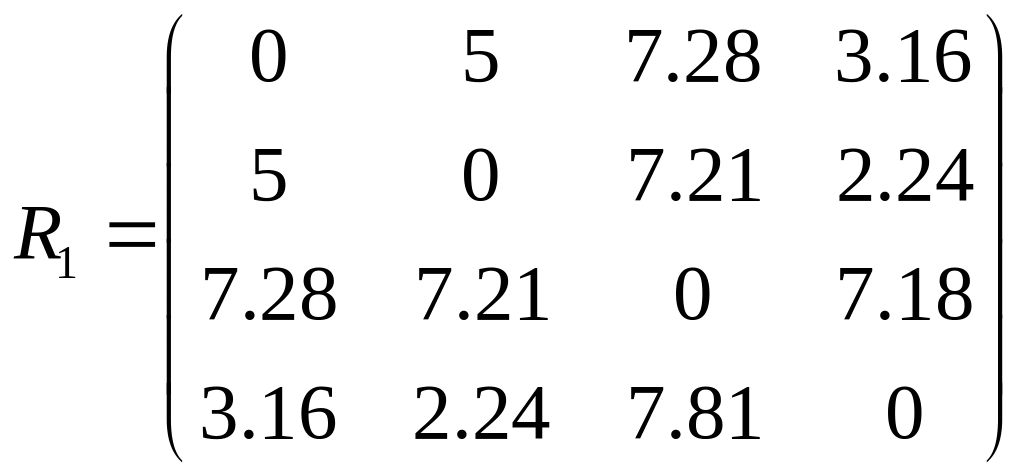
Из матрицы расстояний следует, что объекты 4 и 2 наиболее близки,
ρ4,2=2,24 и поэтому объединим их в один кластер. После объединения объектов имеем четыре кластера:S1, S2, S3, S(4,2).
S(4,2),1=
ρ(S1,
S(4,2))=
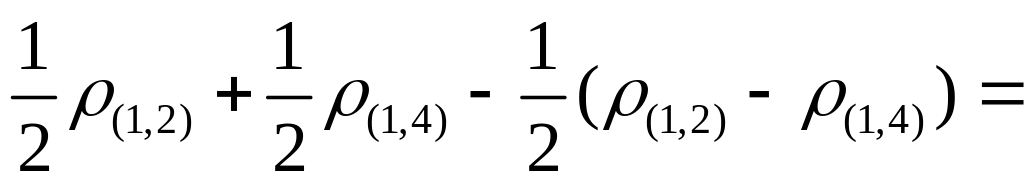3,16
S(4,2,1)S3=
ρ(S3,
S(4,2,1))=
7,21
2.Классификация на основе обычного евклидова расстояния и принципа “дальнего соседа”.
Как и в случае (1), мы используем обычное евклидово расстояние, поэтому матрица R1 остается без изменения. Согласно агломеративному алгоритму объединяются в один кластер объекты 4 и 2, как наиболее близкие ρ4,2=2,24.
S(4,2)1=
ρ(S1,
S(4,2))=
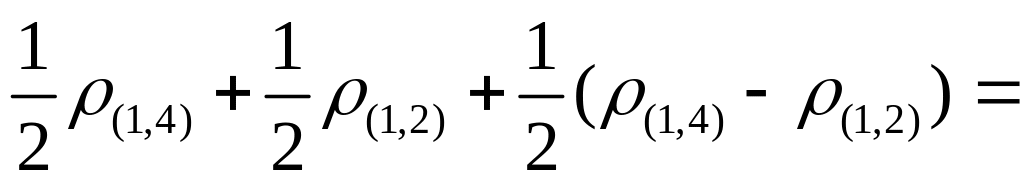5
S(4,2,1)S3=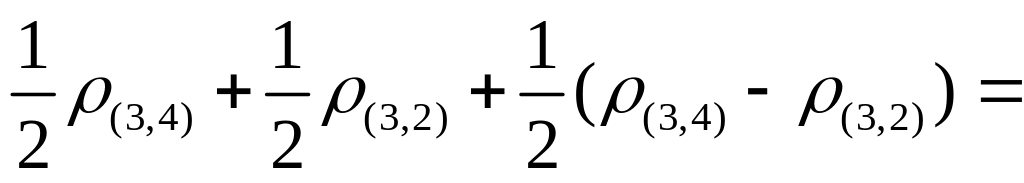
=7,81
3.Классификация на основе обычного евклидова расстояния принцип “центра тяжести ”.
S(2,4)1=4,03
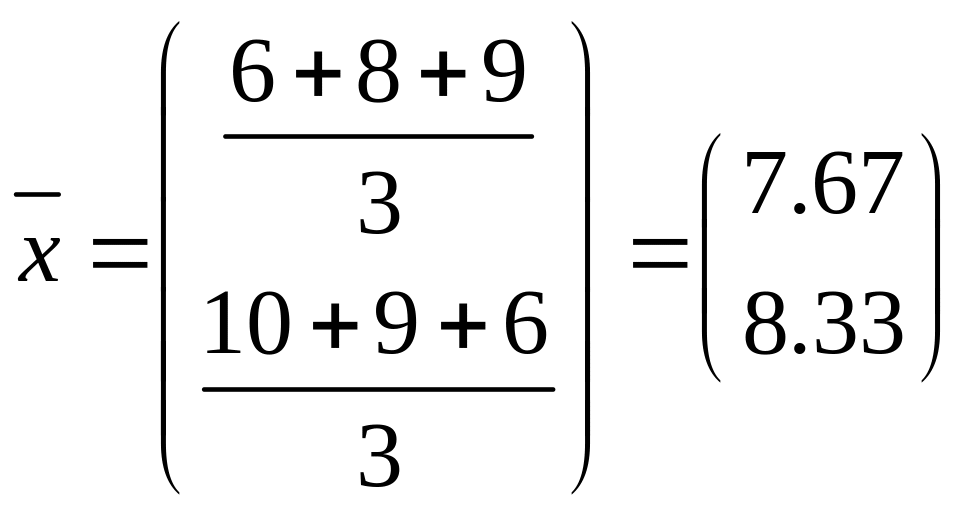
S(2,4,1)(3)=
=7,13
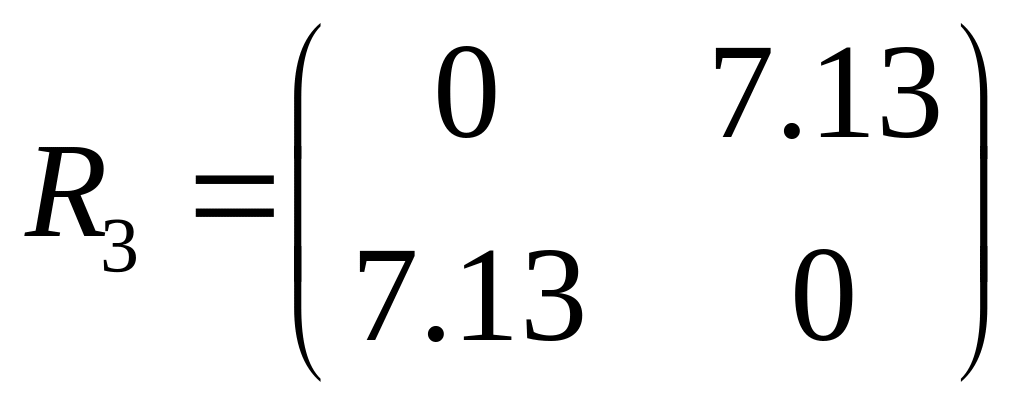
4.Классификация на основе обычного евклидова расстояния принцип «средней связи»
S(4,2)1= ρ(S1, S(4,2))=1/2(ρ (2,4)+ρ (1,4))=4,08
S(2,4)(3)= 1/2(ρ (2,3)+ρ (1,3))=7,51
S(2,4,1)(3)= 1/3(ρ (2,3)+ ρ (4,3)+ρ (1,3))=1/3(7,21+7.81+7,28)=7,43
5.Классификация на основе взвешенного евклидова расстояния принцип “ближайшего соседа”.
Предположим, что показатель х(1) менее важен для классификации, чем х(2). В этой связи припишем им “веса” ω1=0,05 и ω2=0,95
ρ
(1,2)=
=3.96
ρ (2,1)= =3.96
ρ
(2,3)=
=5.92
ρ (3,2)= =5.92
ρ
(1,3)=
=2.5
ρ (3,1)= =2.5
ρ
(1,4)=
=2.93
ρ (4,1)= =2.93
ρ
(2,4)=
=1.07
ρ (4,2)= =1.07
ρ
(3,4)=
=5.05
ρ (4,3)= =5.05
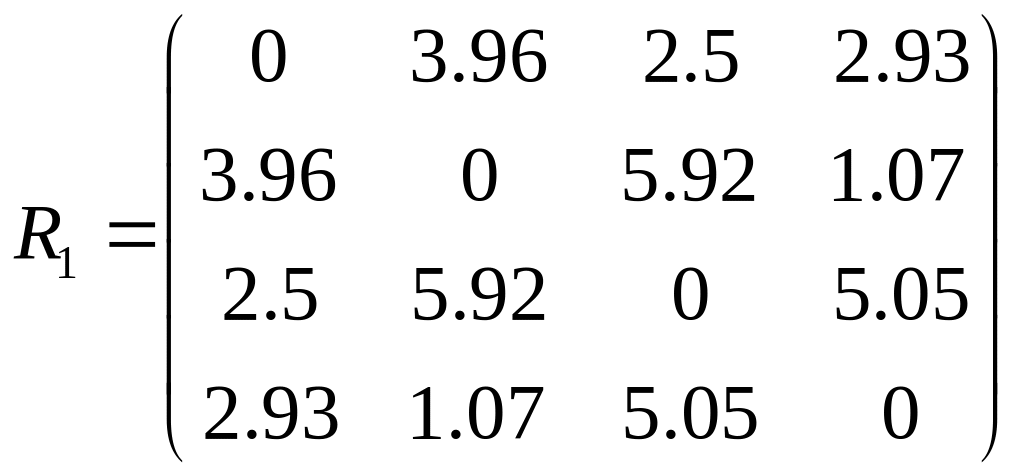
S(4,2),1= ρ(S1, S(4,2))= 2.93
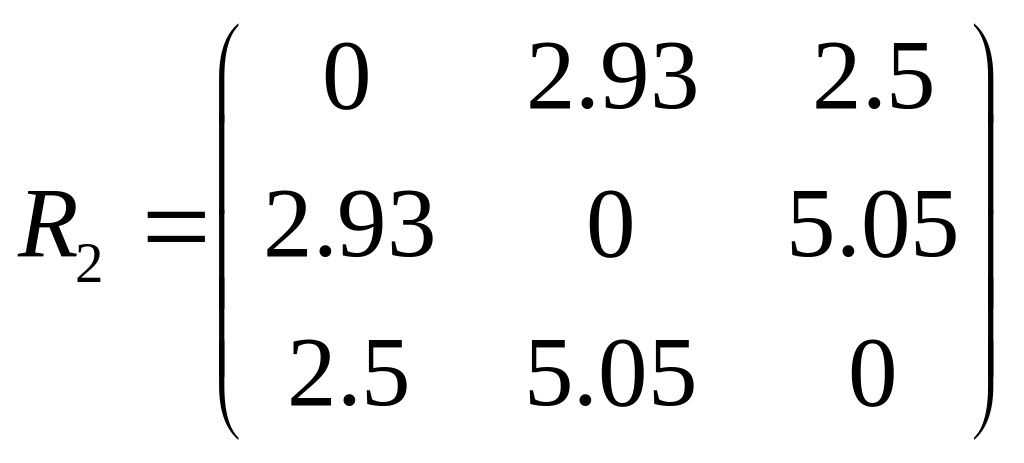
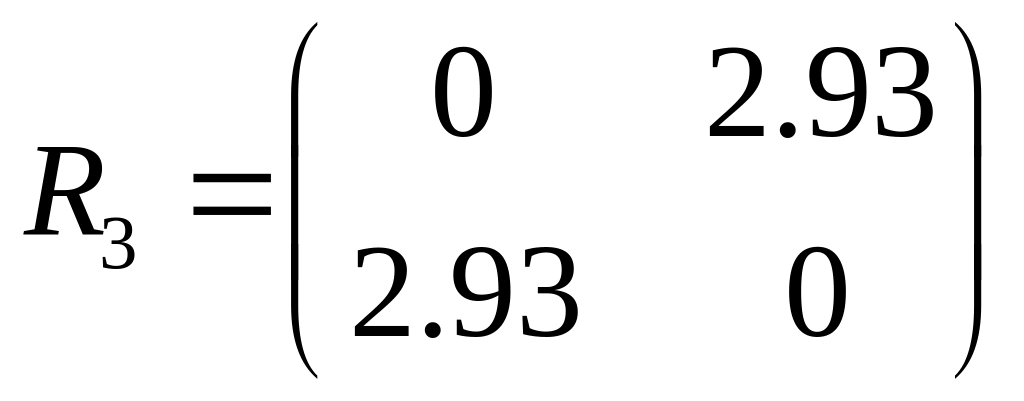
6.Классификация на основе взвешенного евклидова расстояния принцип “дальнего соседа”.
S(4,2)1= ρ(S1, S(4,2))= 3.96
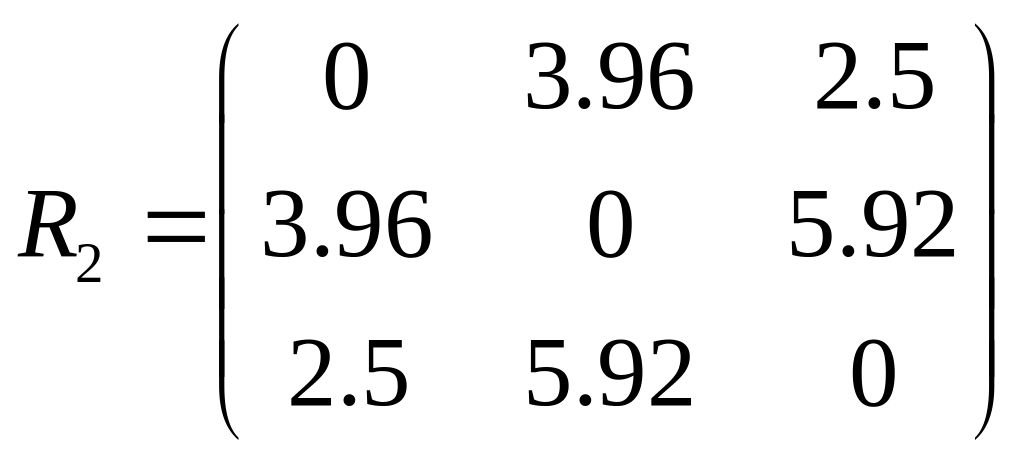
S(4,2,1)S3= =5.92
7.Классификация на основе взвешенного евклидова расстояния принцип “центра тяжести ”.
S(2,4)1=3.42
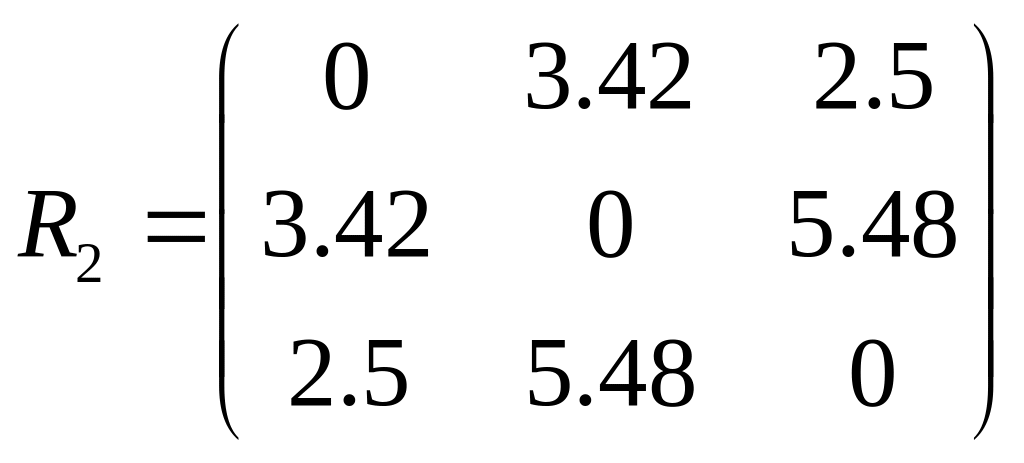
S(2,4,1)(3)=
=5.4
S(2,4,1)(3)=
=4.41
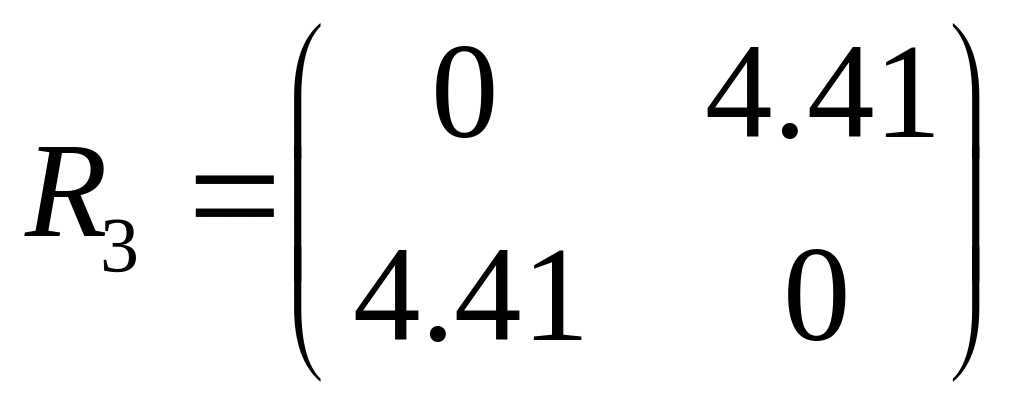
8.Классификация на основе взвешенного евклидова расстояния принцип «средней связи»
S(4,2)1= ρ(S1, S(4,2))=1/2(ρ (2,4)+ρ (1,4))=3.44
S(2,4)(3)= 1/2(ρ (2,3)+ρ (1,3))=5.49
S(2,4,1)(3)= 1/3(ρ (2,3)+ ρ (4,3)+ρ (1,3))=4.43
Отдадим предпочтение разбиению на 2 кластера S(3) и S(1,2,4)