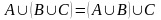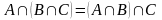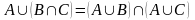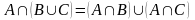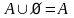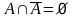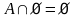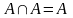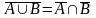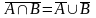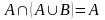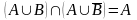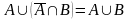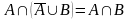5. Понятие совершенной днф. Методика представления булевой функции в виде совершенной днф.

Совершенные нормальные формы

Определение. Совершенной дизъюнктивной формулой формулы алгебры высказываний (СДНФ) называется ДНФ, в которой:

различны все члены дизъюнкции;

различны все члены каждой конъюнкции;

ни одна конъюнкция не содержит одновременно переменную и отрицание этой переменной;

каждая конъюнкция содержит все переменные, входящие в формулу,

Теорема. Пусть f(x₁, x₂, …, x_k) k-местная булева функция. Если f не равна тождественно нулю, то существует такая формула F, зависящая от списка переменных x₁, x₂, …, x_n и находящаяся в СДНФ относительно этого списка, что F выражает собой функцию f. Формула F определена однозначно с точностью до перестановки дизъюнктивных членов.

6. Понятие совершенной кнф. Методика представления булевой функции в виде совершенной кнф.

Определение. Совершенной конъюнктивной формулой формулы алгебры высказываний (СКНФ) называется КНФ, в которой:

различны все члены конъюнкции;

различны все члены каждой дизъюнкции;

ни одна дизъюнкция не содержит переменную вместе с отрицанием этой переменной;

каждая дизъюнкция содержит все переменные, входящие в исходную формулу

Теорема 2. Пусть f(x₁, x₂, …, x_k) k-местная булева функция. Если f не равна тождественно единице, то существует такая формула F, зависящая от списка переменных x₁, x₂, …, x_k и находящаяся в СКНФ относительно этого списка, что F выражает собой функцию f. Формула F определена однозначно с точностью до перестановки конъюнктивных членов.

7. Понятие минимальной ДНФ. Методика представления булевой функции в виде минимальной КНФ.

Определение. Минимальной ДНФ (МДНФ) функции f(x₁, x₂, …, x_n) называется ДНФ, реализующая функцию f и содержащая минимальное число символов переменных по сравнению со всеми другими ДНФ, реализующими функцию f.

8. Операция двоичного сложения и ее свойства. Многочлен Жегалкина. Методика представления булевой функции в виде многочлена Жегалкина.

9. Полнота множества функций. Важнейшие замкнутые классы. Теорема Поста.

10. Понятие множества. Конечные и бесконечные множества, пустое множество. Подмножество; количество подмножеств конечного множества. Теоретико-множественные диаграммы. Операции над множествами и их свойства.

Множество – простейшее, неопределенное понятие. Совокупность элементов рассматриваемых как единое целое – множество. Объекты из которых состоит множество называют элементами данного множества. Множества обозначают большими буквами латинского алфавита, элементы – малыми. При задании множеств перечислением обозначения элементов обычно заключают в фигурные скобки и разделяют запятыми. Перечислением можно задавать только конечные множества (число элементов множества конечно, в противном случае множество называется бесконечным). М={1, 2, 3, 4} Бесконечные множества задаются характеристическим предикатом или порождающей процедурой: 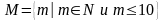- характеристический предикат ; Числа Фибоначчи задаются условиями (порождающей процедурой):а₁=1, а₂=2, a_n=a_n-1+a_n-2 для n>2.

Пустое множество – множество для которого никакой объект не является его элементом называется пустым, или множество в котором вовсе нет элементов. Пустое множество считается подмножеством любого другого множества.

Подмножество – множество А называется подмножеством множества В и обозначается АсВ, если любой элемент множества А принадлежит множеству В.

Два множества считаются равными если они состоят из одних и тек же элементов: А = В. Множество U называется универсальным, то есть все рассматриваемые множества являются его подмножеством

Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):

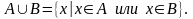
Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):

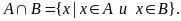
Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):

Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):

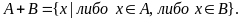
Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А (рис. 5):

1. Коммутативность объединения	1’. Коммутативность пересечения
2. Ассоциативность объединения	2’. Ассоциативность пересечения
3. Дистрибутивность объединения относительно пересечения	3’. Дистрибутивность пересечения относительно объединения
4. Законы действия с пустым и универсальным множествами	4’. Законы действия с пустым и универсальным множествами
5. Закон идемпотентности объединения	5’. Закон идемпотентности пересечения
6. Закон де Моргана	6’. Закон де Моргана
7. Закон поглощения	7’. Закон поглощения
8. Закон склеивания	8’. Закон склеивания
9. Закон Порецкого	9’. Закон Порецкого
10. Закон двойного дополнения