Свойство

Композиция иньективных функций является иньективной функцией

Композиция сюрьективных функций является сюрьективной функцией

Композиция биекций есть биекция

23. Понятие отображения. Обратное отображение. Композиционная степень отображения.

Пусть А и Б не пустые множества R c AxB. Бинарное отношение на паре множеств А и Б называется функцией (отображением) из А в Б если для каждого элемента а из множества А сушествует единственный элемент в из множества В (а,в принадлежит R).

Обозначение: f g h

Пусть f фунция из А в В. Для любого а из множества А, сушествует единстьвенный в из множества В: (а,в) принадлежит R, (а,в) принадлежит f. в = F(а) в – образ элемента а при отображении F, а – прообраз элемента в. Образ всегда один, прообраз один, F: А --» В

F = {(а, f(а) /а принадлежит А}

Функция f из А в В называется обратимой если существует функция g из В в А такая, что выполняются два условия: f(g(b)) = b для всех b из множества В, g(f(a)) = a для всех а из множества А.

Всякая функция f имеет не более одной обратной, то есть не имеет обратной или есть единственная.

Функция f обратима тогда и только тогда когда она является биекцией.

24. Понятие подстановки. Произведение подстановок.

В математике и компьютерных науках подстановка — это операция синтаксической замены подтермов данного терма другими термами, согласно определённым правилам. Обычно речь идёт о подстановке терма вместо переменной.

Подстановка переменной (англ. substitution) в аппликативном программировании понимается следующим образом. Для вычисления значения функции f на аргументе v применяется запись f(v)}, где f определена конструкцией f(x) = e. Запись f(v) в этом случае означает, что в выражении e происходит замещение, или подстановка переменной x на v. Выполнение замещения происходит в соответствии с семантикой вычислений.

Подстановка переменной (англ. assignment) в программировании понимается как присваивание. Оператор присваивания является проявлением эффекта «бутылочного горлышка» фон Нейманна для традиционных языков программирования^[1]. От этого свободны аппликативные вычислительные системы.

25. Понятие подстановки. Обратная подстановка.

В математике и компьютерных науках подстановка — это операция синтаксической замены подтермов данного терма другими термами, согласно определённым правилам. Обычно речь идёт о подстановке терма вместо переменной.

Подстановка переменной (англ. substitution) в аппликативном программировании понимается следующим образом. Для вычисления значения функции f на аргументе v применяется запись f(v)}, где f определена конструкцией f(x) = e. Запись f(v) в этом случае означает, что в выражении e происходит замещение, или подстановка переменной x на v. Выполнение замещения происходит в соответствии с семантикой вычислений.

Подстановка переменной (англ. assignment) в программировании понимается как присваивание. Оператор присваивания является проявлением эффекта «бутылочного горлышка» фон Нейманна для традиционных языков программирования^[1]. От этого свободны аппликативные вычислительные системы.

26. Понятие вычета по модулю N; система вычетов по модулю N. Операции над вычетами (сложение, вычитание, умножение) и их свойства.

27. Проблема криптографической защиты информации; понятие шифрования.

28. Шифры замены. Шифр Цезаря и шифр Виженера как частные случаи шифров замены.

Шифры простой замены

В шифрах простой замены замена производится только над одним единственным символом. Для наглядной демонстрации шифра простой замены достаточно выписать под заданным алфавитом тот же алфавит но в другом порядке или например со смещением. Записанный таким образом алфавит называют алфавитом замены.

Шифр Цезаря, также известный как шифр сдвига, код Цезаря или сдвиг Цезаря — один из самых простых и наиболее широко известных методов шифрования.

Шифр Цезаря — это вид шифра подстановки, в котором каждый символ в открытом тексте заменяется буквой находящейся на некоторое постоянное число позиций левее или правее него в алфавите. Например, в шифре со сдвигом 3, А была бы заменена на Г, Б станет Д, и так далее.

Шифр назван в честь римского императора Гая Юлия Цезаря, использовавшего его для секретной переписки со своими генералами.

Шаг шифрования, выполняемый шифром Цезаря, часто включается как часть более сложных схем, таких как шифр Виженера, и все еще имеет современное приложение в системе ROT13. Как и все моноалфавитные шифры, шифр Цезаря легко взламывается и не имеет практически никакого применения на практике.

Шифр Виженера (фр. Chiffre de Vigenère) — метод полиалфавитного шифрования буквенного текста с использованием ключевого слова.

Шифр Виженера достаточно прост для использования в полевых условиях, особенно если применяются шифровальные диски. Например, «конфедераты» использовали медный шифровальный диск для шифра Виженера в ходе Гражданской войны. Послания Конфедерации были далеки от секретных, и их противники регулярно взламывали сообщения. Во время войны командование Конфедерации полагалось на три ключевых словосочетания: «Manchester Bluff», «Complete Victory» и — так как война подходила к концу — «Come Retribution».

29. Перестановочные шифры.

Простой перестановочный шифр с фиксированным периодом n подразумевает разбиение исходного текста на блоки по n символов и использование для каждого такого блока некоторой перестановки E. Ключом такого шифра является используемая при шифровании перестановочная матрица P или вектор t, указывающий правило перестановки. Таким образом, общее число возможных ключей определяется длиной блока n и равно n!. При дешифрации используется матрица обратной перестановки D, являющаяся обратной к матрице P по умножению, то есть D*P=I, где I — единичная матрица.

30. Принцип метода математической индукции.

В основе метода математической индукции лежит следующий принцип.

Некоторое утверждение верно при любом натуральном п, если;

1)  оно верно при п = 1

и

2)  из справедливости, этого утверждения при каком-либо произвольном значении  n = k  (k >1 ) следует,  что оно верно и при n = k + 1.

Действительно, при п = 1 утверждение верно в силу 1). Далее, 2 = 1 + 1, а потому в силу 2) утверждение верно при п = 2; 3 = 2+1, поэтому в силу 2) утверждение верно и при п = 3. Вообще, любое натуральное число п может быть получено из 1 путем последовательного прибавления к нему единицы п — 1 раз. При каждом таком прибавлении мы получаем натуральное число, для которого рассматриваемое утверждение верно. Поэтому оно верно и для натурального числа п.

Метод доказательства, основанный на использовании этого принципа, называется методом математической индукции.

Рассмотрим  несколько  примеров.

Пример    1.    Найти  сумму

Сначала найдем суммы одного, двух, трех и четырех слагаемых. Имеем:

В каждом из этих случаев получается дробь, в числителе которой  стоит число слагаемых,  а  в знаменателе — число,   на единицу большее числа слагаемых. Это позволяет высказать гипотезу (предположение), что при любом натуральном п

Для проверки этой гипотезы воспользуемся методом математической   индукции.

1)  При п = 1 гипотеза верна, так как   

2)  Предположим, что гипотеза верна при п = k то есть

Докажем, что тогда гипотеза должна быть верной и при п = k + 1,  то есть

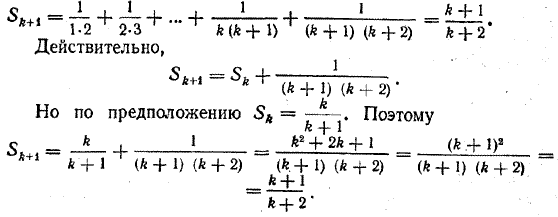
Таким образом, исходя из предположения, что гипотеза    , верна при       п = k , мы доказали, что она   верна и при п = к + 1. Поэтому формула

верна  при  любом  натуральном  п.

Пример 2. Доказать, что n-й член арифметической прогрессии   равен

a_n = a₁+ (п — 1)d,                                (1)

где a₁   — первый член, a d —   разность этой прогрессии.

Этот пример отличается от предыдущего тем, что строить гипотезу здесь не надо, она дана. Нужно только доказать, что эта  гипотеза  верна.

Доказательство будем вести методом математической индукции.

1)  При п = 1 формула (1) имеет вид:

a₁ = a₁

так что при п = 1 эта формула верна.

2)  Предположим, что она верна при п = k, то есть

a_k = a₁+ (k — 1)d,

и покажем, что в таком случае она должна быть верной и при п = k + 1,   то  есть

a_k+1 = a₁+ kd.

Действительно,

a_k+1 = a_k + d = [a₁+ (k — 1)d] + d = a₁+ kd,

что и требовалось доказать.

Оба условия принципа математической индукции выполняются, и потому формула (1) верна для любого натурального числа п.

Пример   3.    Доказать  тождество

(cos α + i sin α)ⁿ = cos пα + i sin пα.                   (2)

1)  При п = 1 обе части формулы (2) принимают   один и тот же вид, cos α + i sin α, так что при п = 1 эта формула    верна.

2)  Пусть она верна при n = k, то есть

(cos α + i sin α)^k = cos kα + i sin kα.

Тогда

(cos α + i sin α)^k+1 = (cos α + i sin α)^k •  (cos α + i sin α) =

= (cos kα + i sin kα) (cos α + i sin α) =

= (cos kα cos α — sin kα sin α)  + i (cos kα sin α + sin kα cos α) =

= cos (kα + α) + i sin (kα + α) = cos (k + l)α + i sin (k + l)α.

Но это означает, что формула (2) верна и при п = k + 1.

Оба условия принципа математической индукции выполняются, и потому формула (2) верна при любом натуральном п.

Пример  4.  Доказать, что при любом натуральном п*

* Если х =/= 0; случай, когда х = 0, требует, строго говоря, специального рассмотрения.

(х^п)'  = пх^п—1              (3)

1)  При n = 1 формула (3) принимает вид: х' = 1.

Это соотношение, как было доказано в главе X, верно. Значит, при п = 1 формула (3) верна.

2)  Предположим, что она верна при п = k, то есть (х^k)'  = kх^k—1,  и,  исходя из этого, докажем, что она должна быть верна и при п = k + 1, то есть (х^k+1)'  = (k +1)х^k . Действительно, представляя х^k+1   в виде х^k • х   и   используя правило дифференцирования произведения, получаем:

(х^k+1)'  = (х^k • х)' = (х^k)' х + х^k • (х)'.

Но по предположению (х^k)'  = kх^k—1, к тому же  х'= 1. Поэтому

(х^k+1)'  = kх^k—1 •  х + х^k •1 = (k + 1) х^k.

Итак, оба условия принципа математической индукции выполняются, и потому формула (3) верна при любом натуральном п.

31. Понятие неориентированного графа. Способы задания графа. Матрица смежности. Путь в графе. Цикл в графе. Связный граф. Компоненты связности графа.

Две вершины, связанные между собой ребром, равноправны, и именно поэтому такие графы называются неориентированными: нет никакой разницы между "началом" и "концом" ребра.

Цикл - это замкнутый путь. Все вершины в цикле, кроме первой и последней, должны быть различны.

Путь в графе - это последовательность вершин (без повторений), в которой любые две соседние вершины смежны

Матрица смежности Sm - это квадратная матрица размером NxN ( N - количество вершин в графе ), заполненная единицами и нулями по следующему правилу:

Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u,v] = 1, в противном случае Sm[u,v] = 0.

Заметим, что данное определение подходит как ориентированным, так и неориентированным графам: матрица смежности для неориентированного графа будет симметричной относительно своей главной диагонали, а для орграфа - несимметричной.

Граф называется связным, если все его вершины взаимно достижимы.

Компонента связности - это максимальный связный подграф. В общем случае граф может состоять из произвольного количества компонент связности. Заметим, что любая изолированная вершина является отдельной компонентой связности. На рис. 11.4 изображен граф, состоящий из четырех компонент связности: [abhk], [gd], [c] и [f].

32. Понятие неориентированного графа. Степень вершины. Теорема о сумме степеней вершин графа.

Две вершины, связанные между собой ребром, равноправны, и именно поэтому такие графы называются неориентированными: нет никакой разницы между "началом" и "концом" ребра.

Любому ребру инцидентно ровно две вершины, а вот вершине может быть инцидентно произвольное количество ребер, это количество и определяет степень вершины. Изолированная вершина вообще не имеет инцидентных ей ребер (ее степень равна 0 ).

33. Понятие неориентированного графа. Полный граф; формула количества рёбер в полном графе.

Две вершины, связанные между собой ребром, равноправны, и именно поэтому такие графы называются неориентированными: нет никакой разницы между "началом" и "концом" ребра.

Полный граф — простой граф, в котором каждая пара различных вершин смежна.

34. Изоморфные графы. Методика проверки пары графов на изоморфность.

Изоморфные графы(Isomorphic graphs) - графы, между которыми установлено отношение изоморфизма; другими словами, графы G и H изоморфны (G H), если существует изоморфизм графа G на граф H

Изоморфизм графов(Graph isomorphism) - биекция : V(G) V(H) множества вершин графа G на множество вершин графа H, сохраняющая отношение смежности; другими словами, для любых вершин u и v графа G их образы (u) и (v) смежны в H тогда и только тогда, когда u и v смежны в G. Отношение изоморфизма графов является эквивалентностью, т.е. оно симметрично, транзитивно и рефлексивно. Следовательно, множество всех графов разбивается на классы так, что графы из одного класса изоморфны, а графы из разных классов не изоморфны. Задача установления изоморфизма графов есть NP-полная проблема. Топорное объяснение на пальцах. Допустим у тебя есть два графа и у каждого занумерованы вершины. Так вот, эти графы изоморфны, если у одного из этих графом можно перенумеровать вершины так, что ребра у них станут одинаковы (ребра задаются парой номеров вершин). Корявому объяснению - корявый пример: Граф 1: вершины 1, 2, 3 ребра 1 - 2, 1 - 3 Граф 2: вершины 1, 2, 3 ребра 1 - 2, 2 - 3. Если во втором графе мы перенумеруем вершины, поменяв 1 и 2 местами, то мы получим ребра 2 - 1 и 1 - 3, т.е. такие же, как и в первом графе. Короче говоря, графы изоморфны, если они "одинаково выглядят".