22. Модели линейного программирования (постановка задачи, математическая модель, решение графическим методом).

Линейные задачи (Задачи линейного программирования).

В основе задач линейного программирования лежит математическая модель, т.е. и целевая ф-я и все ограничения линейны.

Определение 1: Задача в которой необходимо максимизировать или минимизировать линейную форму при условии что выполняется соотношение: и может иметь место и называется задачей линейного программирования в произвольной форме.

Определение 2: Задача, в которой необходимо максимизировать или минимизировать линейную форму при условии что имеется следующий набор ограничений и называется задачей линейного программирования в стандартной форме.

В литературе задачи линейного программирования часто записываются в матричной форме:

- целевая ф-ия.

Определение 3: Задача в которой необходимо максимизировать или минимизировать линейную форму при условии что: , называется задачей линейного программирования в канонической форме.

Правила сведения произвольной задачи к канонической: в канонической задаче лин-го программирования все ограничения должны иметь форму равенств с неотрицательной правой частью. Для этого используют следующий прием:

1. Если в задаче, записанной в произвольной форме, какое – либо ограничение имеет отрицательную правую часть, то умножаем всё ограничение на (-1)

2. Если в задаче заданной произвольной форме ограничения имеют вид неравенств, то они превращаются в равенства путем введения дополнительных переменных. Для неравенства типа ”≥” вводится избыточная переменная, для нер-ва типа “≤” остаточная переменная.

3. Если в задаче записанной в произвольной форме свободные переменные, то они расписываются след. образом: при этом

Вектор X=(X₁,….,X_n) удовлетворяющий ограничениям задачи линейного программирования называется ее планом(допустимым решением).

Решением задачи линейного программирования называется ее план максимизирующий (минимизирующий) целевую функцию.

В общем случае задача линейного программирования, записанная в канонической форме имеет m уравнений и n неизвестных переменных (m<n) поэтому при решении задачи возникает такое понятие как базисное решение, т.е. при решении системы уравнений где количество неизвестных больше чем количество уравнений мы произвольные m неизвестных считаем базисными, а оставшиеся (n-m) неизвестных считаем небазисными. Для того чтобы решение для m базисных переменных было базисным необходимо чтобы оно было положительным и единственным.

При решении системы ур-ий для m базисных переменных оставшиеся (n-m) переменных полагаются равными нулю.

В общем случае количество допустимых базисных переменных определяется сочетанием:

Графически метод решения задач линейного программирования.

Графический метод решения применяется для задач в которых имеется только 2 неизвестных величины. На практике при решении реальных задач его удается применить крайне редко. Тем не менее, на этом методе основаны другие методы решения задач линейного программирования. Суть графического метода заключается в следующем:

1. На плоскости с помощью всех ограничений задачи строится пространство допустимых значений.

2. В пространстве допустимых значений определяются все узловые точки.

3. С помощью целевой функции среди угловых точек определяется точка оптимального решения.

Пространством допустимы решений будем называть часть плоскости, все точки которой удовлетворяют всем ограничениям задачи. В линейной задаче пространство допустимых решений всегда выпуклое. В выпуклом множестве целевая функция достигает экстремума только в угловых точках. В общем случае пространство допустимых решений линейной задачи может быть областью типа:

1. 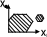- основной случай: область называется ограниченным выпуклым многоугольником.

2 . - неограниченный выпуклый многоугольник

3. Ограничения задачи противоречат друг другу вследствие чего обл. допустимых значений пуста.

Пример: z=c₁x₁+c₂x₂→extr; ; a₁₁x₁+a₁₂x₂≤b₁; a₂₁x₁+a₂₂x₂≥b₂;. . . . . . ;a_m1 x₁+a_m2x₂≥b_n

Угловая точка, которую целевая ф-я проходит последней двигаясь по пространству допустимых решений, будет точкой оптимального решения.