§1.3. Метод планов ускорений

Пример 1. Построим план ускорений (рис.9, б) для механизма подачи суппорта строгального станка.

Исходные данные: l_OA = 0,074 м; l_OB = 0,286 м; l_BC = 0,420 м;

h = 0,460 м; φ₁ = 150⁰; ω₁ = 27 рад/с.

Для решения задачи необходимо предварительно построить план поло­жения и план скоростей механизма. План положения механизма построен на рис. 9, а. План скоростей механизма построен на рис. 5, б. Методика этих по­строений была рассмотрена в параграфах 1.1 и 1.2.

По плану скоростей определили: ω₃ = 4 рад/с; V_A3A1 = 1,5 м/с.

Решение

1. Определим ускорение точки А₁ "пальца" кривошипа. В общем слу­чае

, (11)

где – нормальное ускорение; – тангенциальное ускорение.

Численно ; . По условию задачи кривошип вра­щается равномерно, то есть . Следовательно, его угловое ускоре­ние и . Таким образом, в нашем случае пол­ное ускорение точки А₁ равно ее нормальному ускорению, то есть

. (12)

Численно 27² · 0,074 = 54 м/с².

Вектор направлен вдоль АО от точки А к точке О.

2. Определим ускорение точки А₃ кулисы ВС; составим два векторных равенства:

, (13)

, (14)

где – кориолисово ускорение;

– ускорение относительного движения;

– нормальное ускорение точки А₃ относительно точки В во вращатель­ном движении кулисы BC вокруг B;

– тангенциальное ускорение точки А₃ относительно точки В в этом движе­нии.

Численно . Направление вектора определим, повернув на плане скоростей (рис. 5, б) вектор на в сто­рону вращения кулисы, то есть по ω₃.

Далее вычислим ,

где l_AB = BA·μ_l = 82·0,004 = 0,328 м; длина отрезка BA = 82 мм получена измерением на плане положения механизма. Вектор параллелен ВС; век­тор направлен вдоль ВС от точки А к точке В (рис. 9, а); вектор перпендикулярен ВС.

3. Определим масштабный коэффициент плана ускорений. Введем обо­значения: π ─ полюс плана ускорений; ─ вектор, изображающий на плане ускорений ускорение точки А₁ ─ . Для вычисления масштабного коэф­фициента необходимо задаться длиной вектора . При этом должны вы­полняться следующие условия:

1) длина отрезка 80 мм ≤ πa₁ ≤ 120 мм;

2) длина отрезка πa₁ должна быть кратной величине ускорения .

Примем πa₁ = 135 мм и вычислим масштабный коэффициент плана ус­корений:

54 / 135 = 0,4 [(м/с²)/мм] (15)

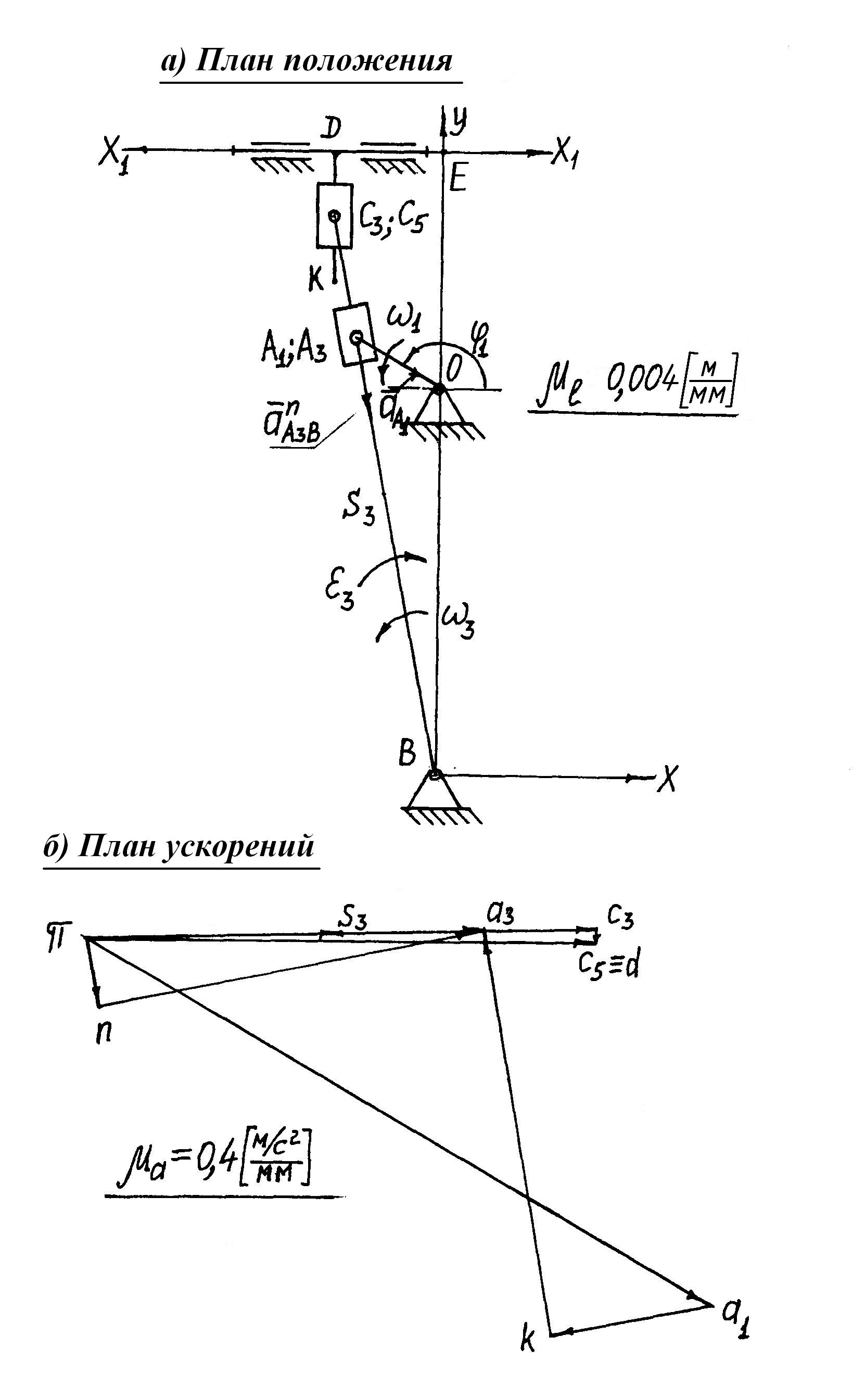
Рис. 9

Вычислим длины отрезков, изображающих на плане ускорения

и :

12 / 0,4 = 30 мм; 5,25 / 0,4 = 13 мм.

4. На основании равенств (13) и (14) проведем построения (рис. 9, б):

◊ из произвольного полюса π проведем луч, параллельный АО в направлении

вектора (см. рис. 9, а); отложим на нем отрезок πa₁=135 мм;

◊ из точки “a₁” проведем луч, перпендикулярный ВС в направлении

(см. рис. 5, б) и отложим на нем отрезок a₁k = 30 мм;

◊ из точки “π ” проведем луч, параллельный ВС в направлении вектора

(см. рис. 9, а), и отложим на нем отрезок πn = 13 мм;

◊ через точку “k ” проведем прямую, параллельную ВС (это линия действия

вектора ), а через точку n – прямую, перпендикулярную ВС (это

линия действия вектора ). На их взаимном пересечении получим точку

“a₃”; соединив ее с полюсом π, получим вектор – ускорение точки

А₃ кулисы в масштабе μ_a.

5. Определим ускорение точки С₃ кулисы. Составим пропорцию для плана ускорений

= BC / BA, (16)

откуда получим

BC / BA = 74 · 105 / 82 = 95 мм,

где длина отрезка πa₃ = 74 мм получена измерением на плане ускорений (рис.9, б); длина отрезка BA = 82 мм получена измерением на плане положения механизма (рис. 9, а); длина отрезка ВС = 105 мм получена вычислением при построении плана положения механизма (см. §1.2, пример 1).

Так как на плане положения механизма точки С₃ и А₃ расположены по одну сторону от оси вращения В, то и на плане ускорений точки “с₃” и ”a₃ ” должны быть расположены также по одну сторону от полюса π. Следова­тельно, точка “с₃” лежит на продолжении πa₃. В соответствии с этим на про­должении луча πa₃ отложим отрезок πс₃ = 95 мм (рис. 9, б).

6. Определим ускорения точек D и C₅; составим векторное равенство:

, (17)

где – ускорение относительного движения; вектор параллелен DK; – абсолютное ускорение всех точек звена 5, движущегося по­ступательно вдоль оси (x – x₁); следовательно, вектор параллелен оси (x – x₁).

7. Продолжим построения (рис. 9, б):

на основании равенства (17) через точку “c₃” проведем прямую, параллель­ную отрезку DK (см. рис. 9, а), а через полюс π – горизонтальную прямую; на их взаимном пересечении получим точку “c₅”, с которой совпадают точки “d” и “s₅”.

8. Используя масштабный коэффициент μ_a, вычислим:

◊ ускорение точки D ползуна 5 95 · 0,4 = 38 м/с²,

где длина отрезка πc₅ = 73 мм – получена измерением на плане ускорений ме­ханизма;

◊ ускорение точки S₃ центра масс кулисы ВС

0,5 · 95 · 0,4 = 19 м/с²,

где πs₃ = 0,5·πc₃; πc₃ = 95 мм (см. пункт 5 решения);

◊ угловое ускорение кулисы ВС

73 · 0,4 / 0,328 = 89 рад/с²,

где длина отрезка na₃ = 73 мм – получена измерением на плане ускорений ме­ханизма; длина отрезка l_AB = 0,328 м вычислена в пункте 2 решения.

Пример 2. Построим план ускорений (рис.11) для второй модели ме­ханизма подачи суппорта строгального станка.

Для решения задачи необходимо предварительно построить план поло­жения и план скоростей механизма.

План положения механизма построен на рис. 10. План скоростей меха­низма построен на рис. 6, б. Методика этих построений была рассмотрена в параграфах 1.1 и 1.2.

Исходные данные: l_OA = 0,050 м; l_OB = 0,100 м; l_ВС = 0,200 м; h = 0,230 м; l_CD = 0,120 м; φ₁ = 240⁰; ω₁ = 36 рад/с.

По плану скоростей определили:

ω₃ = 17,4 рад/с; V_A3A1 = 1,47 м/с; ω₄ = 13,25 рад/с.