
- •Цель и задачи дисциплины
- •План предполагаемого объема часов по темам и видам учебных занятий
- •Основные условные обозначения
- •Раздел I техническая термодинамика
- •Основные положения технической термодинамики.
- •Основные понятия и определения.
- •Основные параметры термодинамики.
- •Физический смысл газовой постоянной
- •2. Основное уравнение кинетической теории газов.
- •3. Состав смеси в массовых и в объемных долях
- •Постоянная теплоемкость
- •Переменная теплоемкость
- •Средняя теплоемкость
- •Теплоемкость при постоянном объеме и давлении
- •Для продуктов горения
- •Для реального газа
- •Теплоемкость смеси газов
- •Вопросы для самоконтроля
- •Внутренняя энергия и её свойства
- •Энтальпия газа
- •Работа газа
- •Вопросы для самоконтроля
- •Изохорный, изобарный, изотермический, адиабатный и политропный процессы.
- •Содержание второго закона термодинамики и его формулировки. Круговые процессы, прямой и обратный цикл. Термический к.П.Д. Цикла. Цикл Карно и холодильный коэффициент.
- •Аналитическое выражение 2-го закона термодинамики. Энтропия газов и диаграмма ts. Статистическое толкование 2-го закона и ошибочность положений Клаузиуса. Термодинамические процессы
- •Изобарный процесс
- •Изотермический процесс
- •Адиабатный процесс
- •Круговые процессы или циклы
- •Цикл Карно (Сади Карно 1824 г.)
- •Обратный цикл Карно
- •Общее свойство обратимых и необратимых циклов
- •Энтропия газов (превращение газов)
- •Диаграмма тs
- •Рассмотрим изотермический процесс
- •Политропные процессы в ts диаграмме
- •Вопросы для самоконтроля
- •Цикл со смешанным подводом тепла (цикл Тринклера).
- •(Цикл Тринклера)
- •(Цикл Отто)
- •(Цикл Дизеля)
- •Вопросы для самоконтроля
- •Влажный воздух как смесь сухого воздуха и водяного пара.
- •Основные параметры влажного воздуха.
- •Диаграмма I-d влажного воздуха
- •Вопросы для самоконтроля
- •Понятие о насадках для истечения паров и газов
- •При адиабатном истечении:
- •Комбинированное сопло Лаваля
- •Истечение водяного пара
- •Вопросы для самоконтроля
- •Процесс образования пара.
- •Диаграммы p-V, t-s и I-s для водяного пара.
- •Основные термодинамические процессы в I-s диаграмме водяного пара.
- •Энтропия процесса получения пара
- •Диаграмма I – s Общий метод решения задач по диаграмме I – s
- •Для всех процессов
- •Вопросы для самоконтроля
- •Цикл Карно для пара
- •Цикл Ренкина
- •Цикл Ренкина c насыщенным паром
- •Цикл Ренкина с перегретым паром
- •Цикл Ренкина с промежуточным перегревом пара
- •Вопросы для самоконтроля
- •Компрессорных машин
- •Рабочий процесс одноступенчатого компрессора и изображение его в p-V и t-s координатах.
- •Работа и мощность на привод компрессора.
- •Термодинамическое обоснование многоступенчатого сжатия.
- •Термодинамическое обоснование многоступенчатого сжатия
- •Вопросы для самоконтроля
- •Сущность процесса.
- •Изменение состояния газа и пара при дросселировании.
- •Эффект Джоуля-Томсона.
- •Вопросы для самоконтроля
- •3. Термические к.П.Д. Циклов и методы их повышения.
- •4. Понятие о бинарных циклах.
- •Работа гту
- •Бинарные циклы
- •Принципиальная схема парогазовой установки и ее ts-диаграмма
- •Преимущества парогазовой установки:
- •Вопросы для самоконтроля
- •Принципиальная схема и цикл паровой компрессионной холодильной установки.
- •Холодопроизводительность.
- •Принцип работы тепловых насосов и отопительный коэффициент.
- •Холод получают:
- •Упрощенный действительный цикл паровой компрессионной холодильной машины
- •Холодопроизводительность
- •Принцип работы тепловых насосов и коэффициент преобразования
- •Вопросы для самоконтроля
- •Раздел II теория теплообмена
- •Основные понятия и определения.
- •Теплопроводность для одно- и многослойных плоскостей различных конфигураций.
- •Основной закон теплопроводности. Закон Фурье.
- •Для реальных:
- •Теплопроводность однородной плоской стенки
- •Теплопроводность многослойной стенки
- •Теплопроводность однослойной цилиндрической стенки
- •Теплопроводность многослойной цилиндрической стенки
- •Вопросы для самоконтроля
- •Факторы процесса теплопередачи
- •Дифференциальное уравнение теплоотдачи
- •Основы теории подобия физических явлений
- •Вопросы для самоконтроля
- •Излучение светящегося пламени
- •Вопросы для самоконтроля
- •Теплопередача
- •Теплопередача через плоскую стенку
- •Теплопередача через многослойную стенку
- •Теплопередача через цилиндрическую стенку
- •Вопросы для самоконтроля
- •Литература
- •Содержание
Изохорный, изобарный, изотермический, адиабатный и политропный процессы.
Содержание второго закона термодинамики и его формулировки. Круговые процессы, прямой и обратный цикл. Термический к.П.Д. Цикла. Цикл Карно и холодильный коэффициент.
Аналитическое выражение 2-го закона термодинамики. Энтропия газов и диаграмма ts. Статистическое толкование 2-го закона и ошибочность положений Клаузиуса. Термодинамические процессы
Изохорный процесс при V = const.
Изобарный процесс при P = const.
Изотермический процесс при T= const.
Адиабатный – процесс, протекающий без теплообмена тела с окружающей средой.
Политропный – PVn = const.
Первые четыре процесса являются частными случаями политропного процесса, в котором нет ярко выраженных характерных особенностей и необходимых условий протекания.
При исследовании термодинамических процессов определяют:
Уравнения протекания процесса в «PV» диаграмме.
Связь между параметрами газа.
Изменение внутренней энергии.
Величину внешней работы.
Количество подведенного (отведенного) тепла.
Изохорный процесс – (изос – равный, хорос – объем)
Э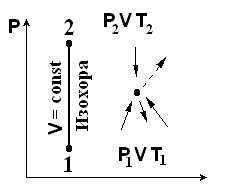 тот
процесс протекает при V = const.
Прямая
тот
процесс протекает при V = const.
Прямая
1-2 – изохора. Термическое состояние газа для точек
1 и 2: P1V = RT1 и
P2V = RT2. Разделим второе уравнение на первое:
![]() (1)
(1)
т.е. в процессе при v = const, изменение давлений прямо пропорционально изменению абсолютных температур:
V1 – V2 = const, следовательно
![]() поэтому ℓ = 0.
поэтому ℓ = 0.
В этом случае уравнение 1-го закона термодинамики:
![]() а т.к.
а т.к.
![]() ,
то:
,
то:
![]()
![]() (2)
(2)
В изохорном процессе все подводимое к газу тепло идет на изменение внутренней энергии, повышение температуры; работа совершается.
Изобарный процесс
Процесс протекает при P = const.
Уравнение состояния газа для точек 1 и 2.
![]()
![]()
Разделим второе уравнение на первое:
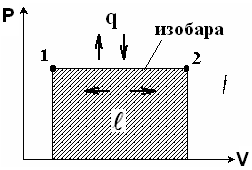
![]() (3)
(3)
В процессе при P = const изменение объемов прямо пропорционально изменению абсолютных температур.
Работа 1 кг газа:
![]() (4)
(4)
т.к.
![]() и
и
![]() ,
и
,
и
![]() ,
то
,
то
![]() (5)
(5)
Изменение внутренней энергии:
![]()
Первый закон термодинамики для процесса P = const.
![]() с учетом (4) и (5)
с учетом (4) и (5)
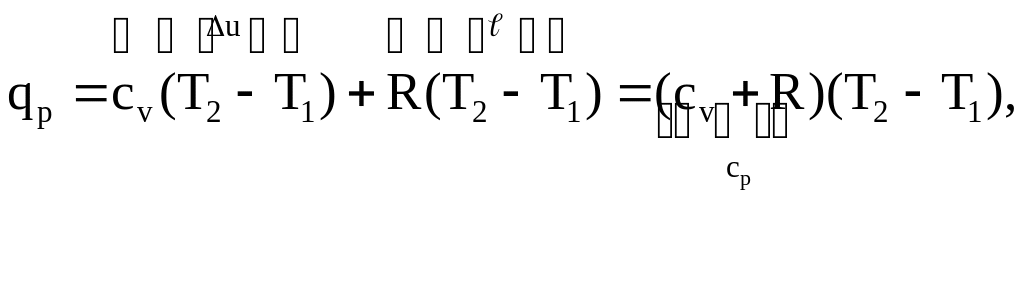 (6)
(6)
а
т.к.
![]() и
и
![]()
то (6) будет:
![]() (7)
(7)
Итак, в изобарном процессе сообщаемое газу тепло идет на увеличение внутренней энергии и совершение внешней работы.
Изотермический процесс
Процесс протекает
при T = const,
т.к.![]() ,
то уравнение изотермы:
,
то уравнение изотермы:
PV = const.
У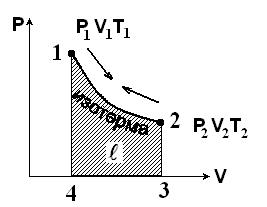 равнение
состояния газа для точек 1 и 2:
равнение
состояния газа для точек 1 и 2:
P1V1 = P2V2 , т.к.
PV = RT = const
или связь между параметрами:
![]()
Работа
1 кг идеального газа: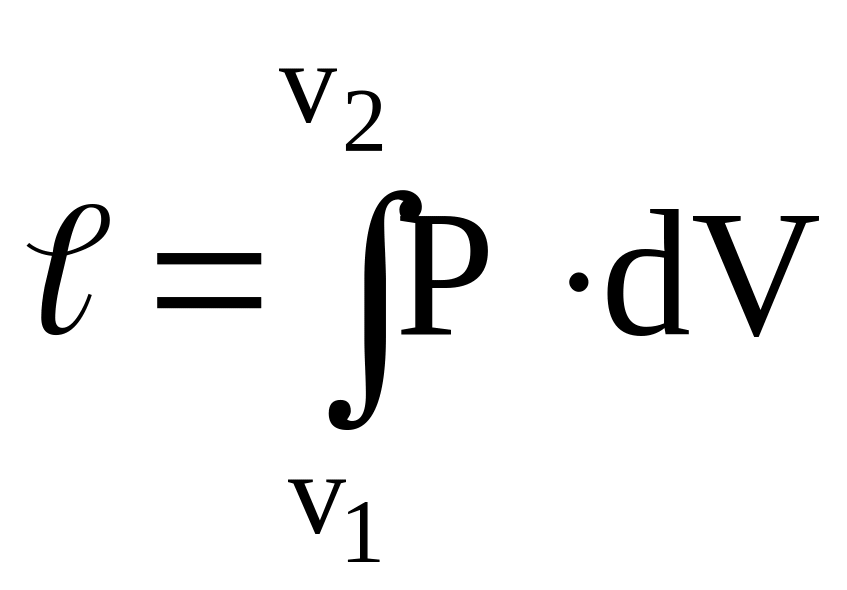 ,
,
но
![]() отсюда:
отсюда:
![]() ,
т.е.
,
т.е.
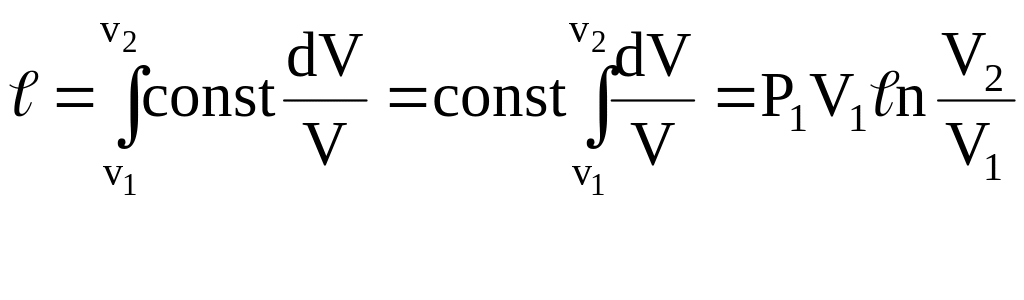
учитывая,
что
![]()
![]() (8)
(8)
2,3 – модуль перехода от натурального логарифма к десятичному.
Изменение внутренней энергии в процессе при T = const:
![]() ,
т.к. T
= const,
тогда выражение 1-го закона термодинамики:
,
т.к. T
= const,
тогда выражение 1-го закона термодинамики:
![]()
т.е.
![]() (10)
(10)
Таким образом, в изотермическом процессе тепло идет на совершение внешней работы.
Адиабатный процесс
Это процесс без обмена теплом с внешней средой, т.е. в этом процессе тепло не подводится к газу из вне и не отдается во вне , т.е.
dq = 0, т.к. q = const.
1-й закон термодинамики:
![]()
т.к.
![]() ,
,
а
![]() ,
то:
,
то:
а)
![]() ,
знаем, что dq = di – VdP,
а
,
знаем, что dq = di – VdP,
а
![]() запишем:
запишем:
б)![]()
Разделим почленно (в) на (а):
![]() а т.к.
а т.к.
![]() то
то
![]() или
или
![]() (13)
(13)
Интегрируем (13) почленно при условии, что к = const, т.к. cp и сv = const.
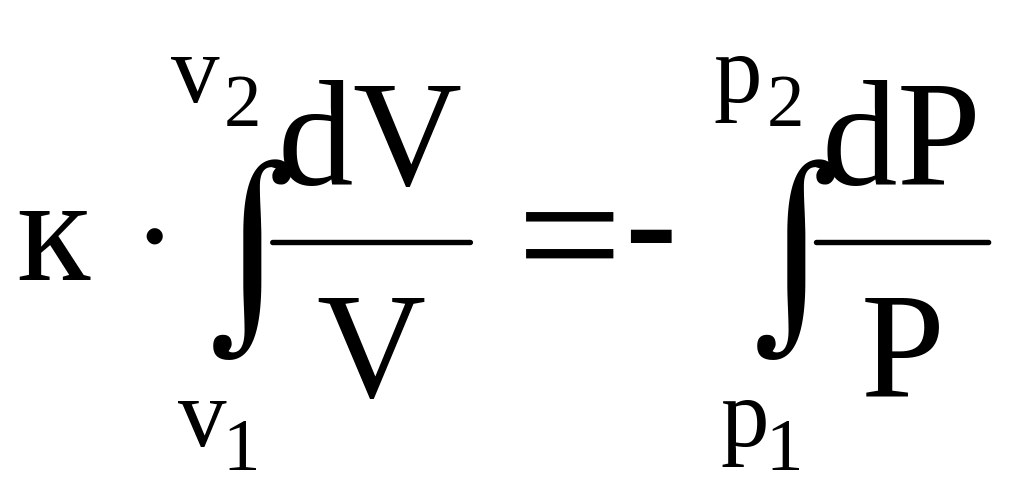 (14)
(14)
![]()
или ![]() (15)
(15)
Это значит, что:
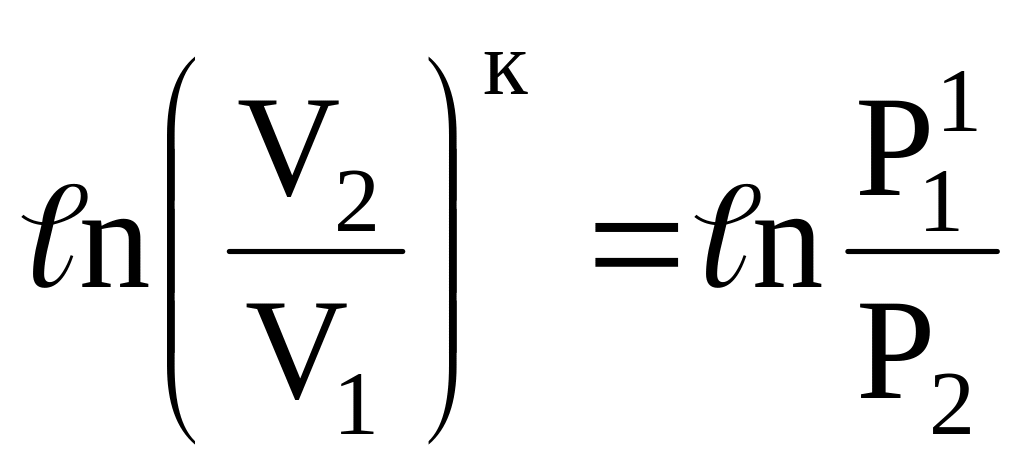 или
или 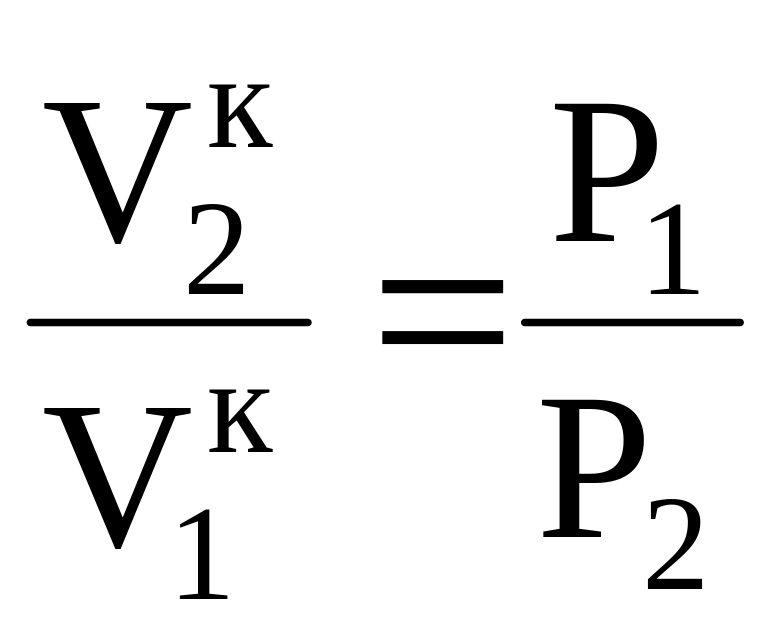
т.е. ![]() (16)
(16)
Следовательно, уравнение адиабаты имеет вид:
![]() (17)
(17)
к – показатель адиабаты
т.к. ср > cv, то к > 1, а PVк = const то это гипербола высшего порядка и идет она круче, чем изотерма.
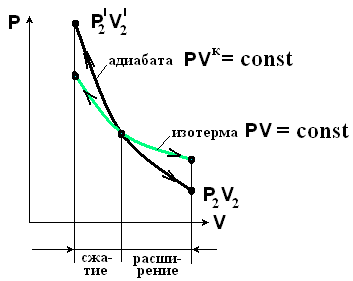
Адиабатный процесс можно совершить в цилиндре с абсолютно нетеплопроводными стенками при бесконечно медленном перемещении поршня.
Процесс
![]() - расширение
- расширение
Процесс
![]() - сжатие.
- сжатие.
Связь между параметрами
Из уравнения адиабаты PVк = const запишем:
![]() или
или
 (18)
(18)
1-й
закон термодинамики:
![]()
отсюда:
![]()
т.к.
![]() ,
то
,
то
![]()
следовательно:
![]() или
или
![]()

(21)
Работа
![]() или
или
![]() (22)
(22)
Используя зависимости:
![]() и
и
![]()
можно записать:
![]()
если
вместо R
подставим его значение
![]() ,
то:
,
то:
![]() (23)
(23)
Изменение внутренней энергии
![]() т.к. q
= 0, то u2
–u1
+ ℓ = 0 и
u1
–u1 = ℓ,
т.к. q
= 0, то u2
–u1
+ ℓ = 0 и
u1
–u1 = ℓ,
т.е. работа расширения в адиабатном процессе происходит за счет внутренней энергии.
Т.к.
![]() ,
то
,
то
![]() ,
т.е. при совершении работы температура
газа падает. При сжатии газа в адиабатном
процессе внутренняя энергия возрастает
и температура повышается.
,
т.е. при совершении работы температура
газа падает. При сжатии газа в адиабатном
процессе внутренняя энергия возрастает
и температура повышается.
Политропный процесс
Этот процесс характеризуется постоянством отношения доли тепла, затрачиваемого на изменение ∆u ко всему теплу, участвующему в процессе:
![]() или
или ![]() а т.к. q
= ∆u
+ ℓ, то
а т.к. q
= ∆u
+ ℓ, то
![]() откуда
откуда
![]()
«α» – как «n» является характеристикой политропного процесса.
Политропный процесс является обобщающим процессом, протекающим при условии, что:
α = const или с = const.
При этом уравнение политропы будет:
![]() ,
(25)
,
(25)
где «n»
– показатель политропы, являющейся для
данного процесса постоянным числом и
принимающий для различных политропных
процессов значения
![]() .
.
Т.к. уравнение политропы (PVn = const) отличается только показателем n, то все соотношения между основными параметрами для адиабаты, а также уравнения работы можно представить теми же формулами, в которых надо величину «к» заменить на «n».
При
этом, если
![]() то
то
![]() (26)
(26)
где сn – теплоемкость в политропном процессе.
Работа в политропном процессе
![]() и
и
![]() (27)
(27)
Тепло для осуществления политропного процесса:
![]()
Теплоемкости:
Для изохорного процесса:
 ;
;Для изобарного процесса:
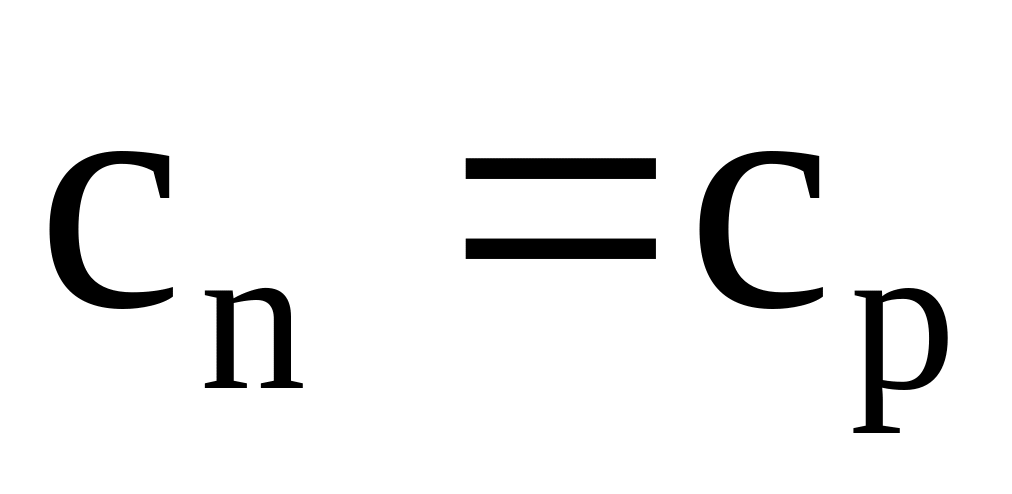 ;
;Для изотермического:
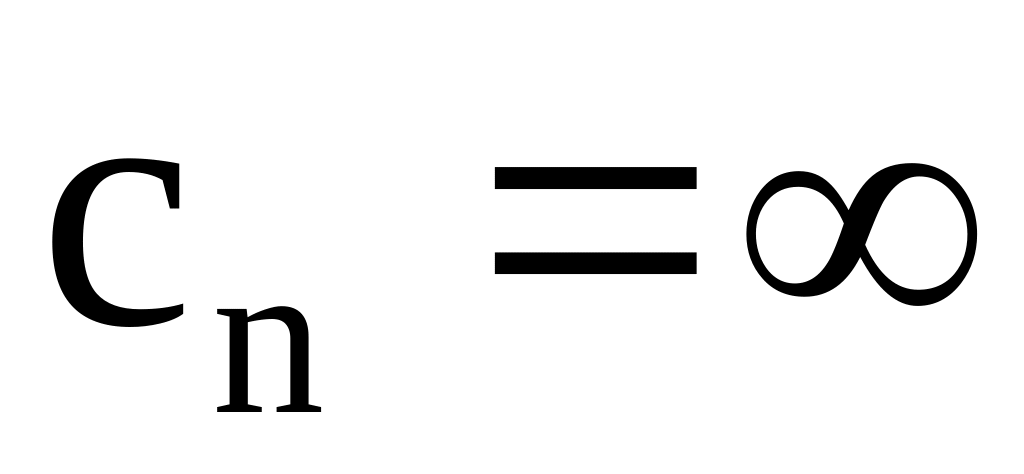 ;
;Для адиабатного:
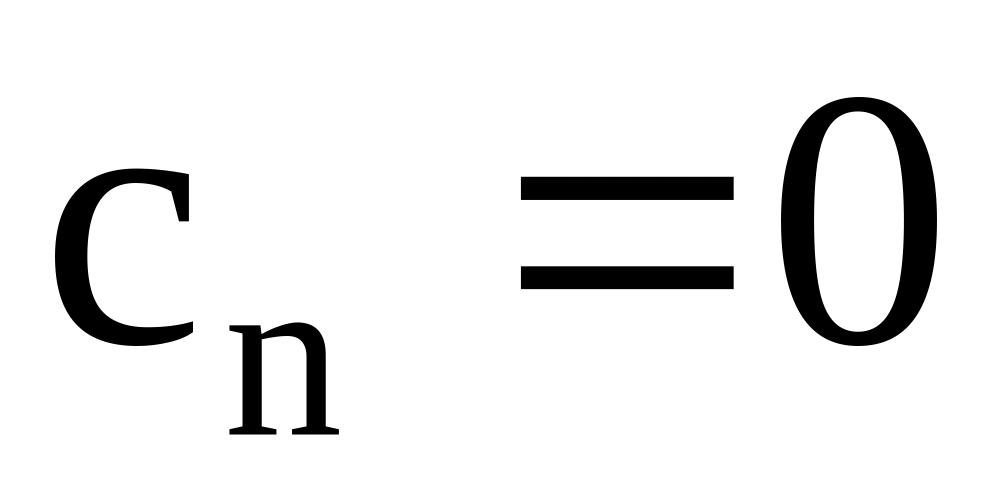 .
.
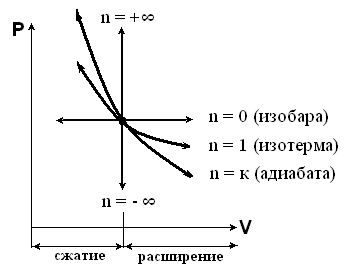
Рабочая диаграмма политропного процесса
Второй закон термодинамики
[I, стр. 49-58]
1-й закон термодинамики устанавливает количественное соотношение между различными видами энергии при их взаимных преобразованиях.
2-й закон термодинамики объясняет, при каких условиях такие превращения могут происходить. Т.н. 2-й закон термодинамики говорит, что невозможно в периодически действующей машине перевести в работу все тепло.
Формулировки 2-го закона термодинамики
1. Клаузиус (1850 г.) |
Теплота не может переходить от холодного тела к более нагретому сама собой даровым процессом без компенсации. |
2. В. Оствальд |
Осуществление вечного двигателя 2-го рода невозможно. |
3. В. Томсон (1851 г.) |
Нельзя построить машину, которая отнимала бы тепло от одного источника и превращала бы его в работу без того, чтобы тело, принимающее участие в рабочих процессах не претерпевало бы каких-либо изменений. |
Таким образом, 2-й закон термодинамики характеризует качественную сторону этих процессов.
