Непрерывная случайная величина.

Функцией распределения называется функция F(x), определяющая вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е.

.

Непрерывной называется случайная величина, имеющая непрерывную, кусочно-дифференцируемую функцию распределения с непрерывной производной.

Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x), равная первой производной от функции F(x):

.

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, называется определенный интеграл

.

Если возможные значения принадлежат отрезку [a; b], то

.

Дисперсией непрерывной случайной величины Х называется математическое ожидание квадрата ее отклонения.

Если возможные значения принадлежат всей оси Ох, то

.

Если возможные значения принадлежат отрезку [a; b], то

.

Формула для вычисления дисперсии, как и в случае дискретной случайной величины:

,

где или .

Среднее квадратическое отклонение непрерывной случайной величины Х определяется, как и для дискретной:

.

Задача 7. Случайная величина Х задана функцией распределения:

Найти математическое ожидание M(X), дисперсию D(X) и среднее квадратическое  (X) отклонение случайной величины. Построить графики функции распределения F(x) и плотности распределения вероятностей f(x).

Решение: Плотность распределения вероятностей f(x) непрерывной случайной величины Х найдем по формуле: . Получим:

Математическое ожидание случайной величины Х найдем по формуле:

.

Дисперсию случайной величины Х найдем по формуле:

,

где .

.

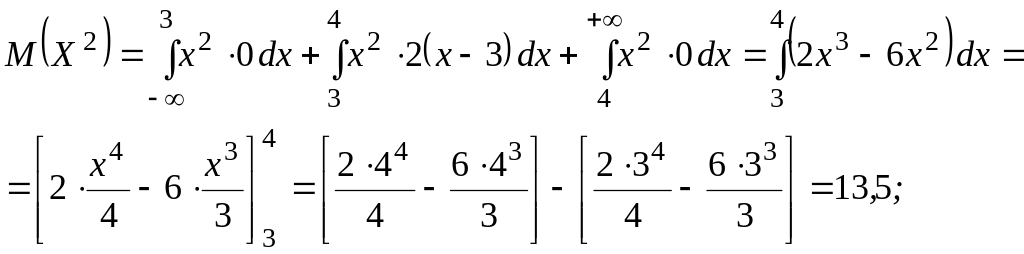
Среднее квадратическое отклонение найдем по формуле:

.

Таким образом, числовые характеристики данного закона распределения:

; ; .

Построим графики функции распределения F(x) и плотности распределения вероятностей f(x):

Рис. 1. График функции распределения.

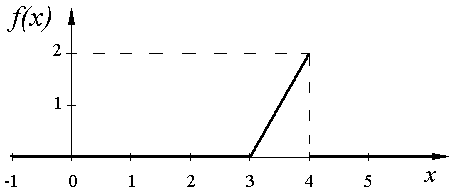
Рис.2. График плотности распределения вероятностей.

Нормальное распределение

Если плотность распределения (дифференциальная функция) случайной переменной определяется выражением:

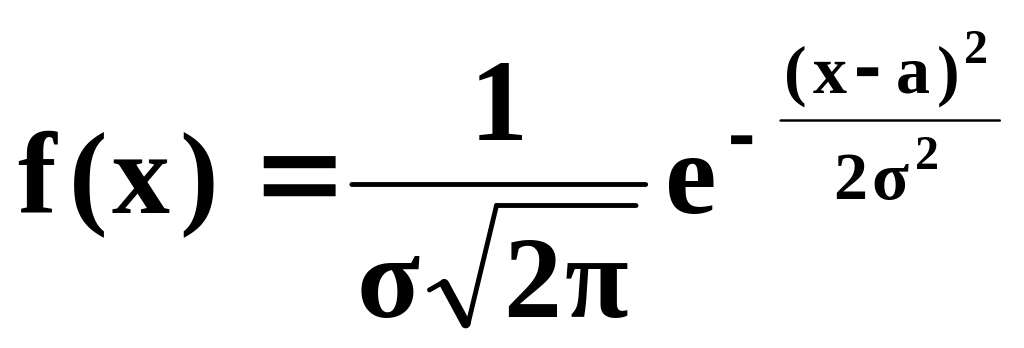
то говорят, что Х имеет нормальное распределение с параметрами а и . Вероятностный смысл параметров: =М(X), а .

Для расчета вероятности попадания нормально распределенной случайной величины Х в промежуток от до используется формула:

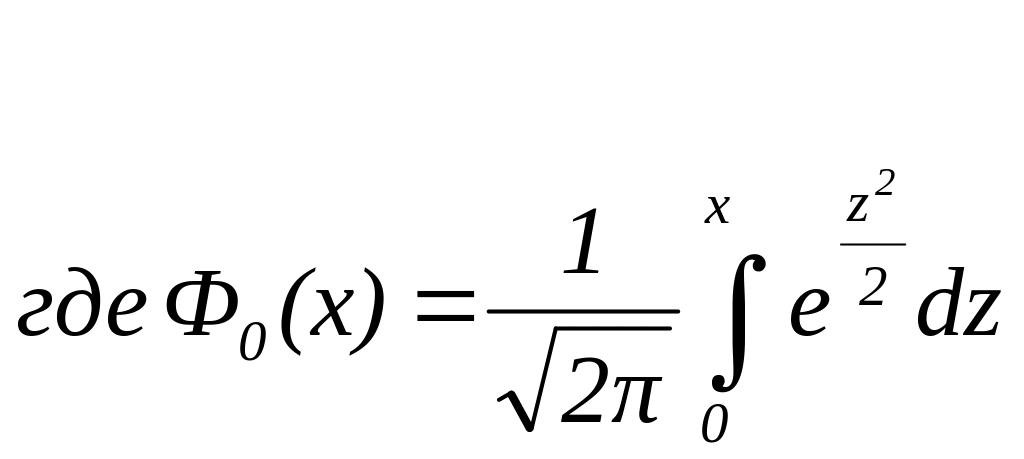(интеграл Лапласа)

Функция табулирована и обладает свойствами:

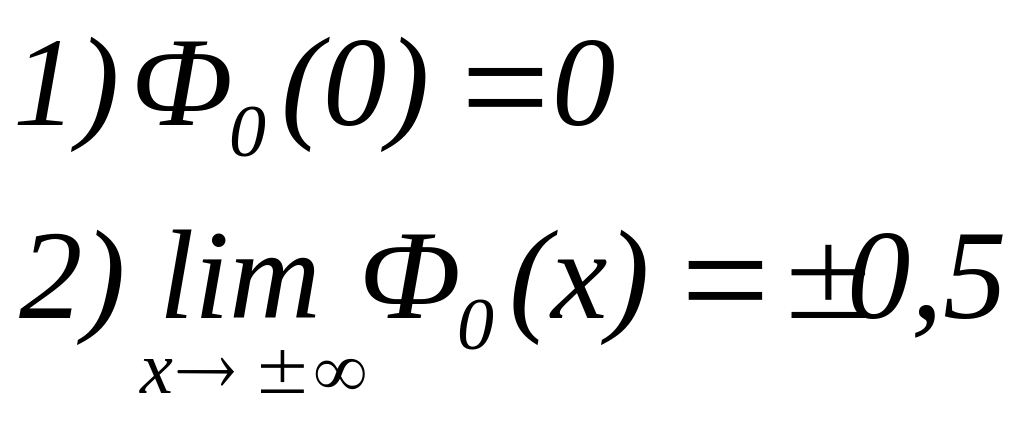
3) .

В частности для симметричного относительно а промежутка имеем:

Формула применима и к частоте m, поскольку ее закон распределения при достаточно большом числе испытаний практически совпадает с нормальным. Применительно к случайной величине m, с учетом ее числовых характеристик

M(m) = np и

формула примет вид :

Формула может быть применена и к относительной частоте с числовыми характеристиками и

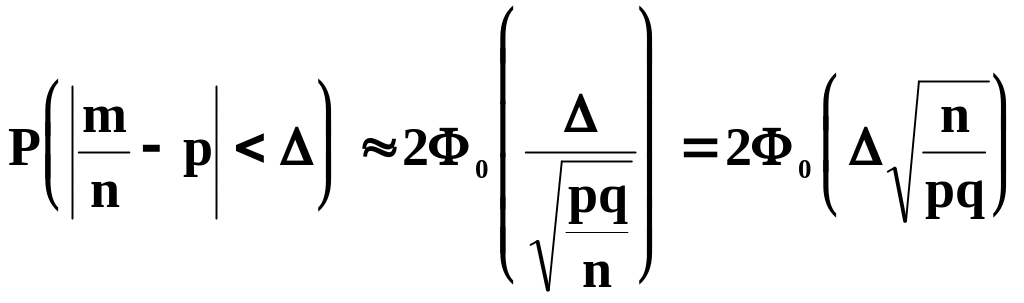
С вероятностью, очень близкой к единице (равной нормально распределенная случайная величина Х удовлетворяет неравенству:

В этом состоит правило трех сигм: если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает .