
- •V Качество процессов регулирования
- •§1 Показатели качества в линейных системах
- •§2 Корневые методы оценки качества
- •§ 3. Частотные методы оценки качества
- •Максимум перерегулирования при невозрастающей вчх (рис.5)
- •4 Интегральные методы оценки качества.
- •§ 5. Оценка качества процессов регулирования в установившихся режимах
- •VII дискретные линейные системы автоматического регулирования
- •1.Классификация дискретных систем
- •3 Математическая модель реального импульсного элемента
- •§ 4. Теорема Котельникова.
- •5. Передаточные функции разомкнутых систем.
- •6. Передаточные функции замкнутых систем.
- •§8 Качество процессов регулирования в импульсных системах
3 Математическая модель реального импульсного элемента
Для облегчения исследования импульсных систем их реальные импульсные элементы СИЭ заменяют математической моделью, которую представляют в виде последовательного соединения простейшего импульсного элемента ПИЭ и формирующего элемента ФЭ (рисунок 1). РИЭ=ПИЭ+ФЭ.
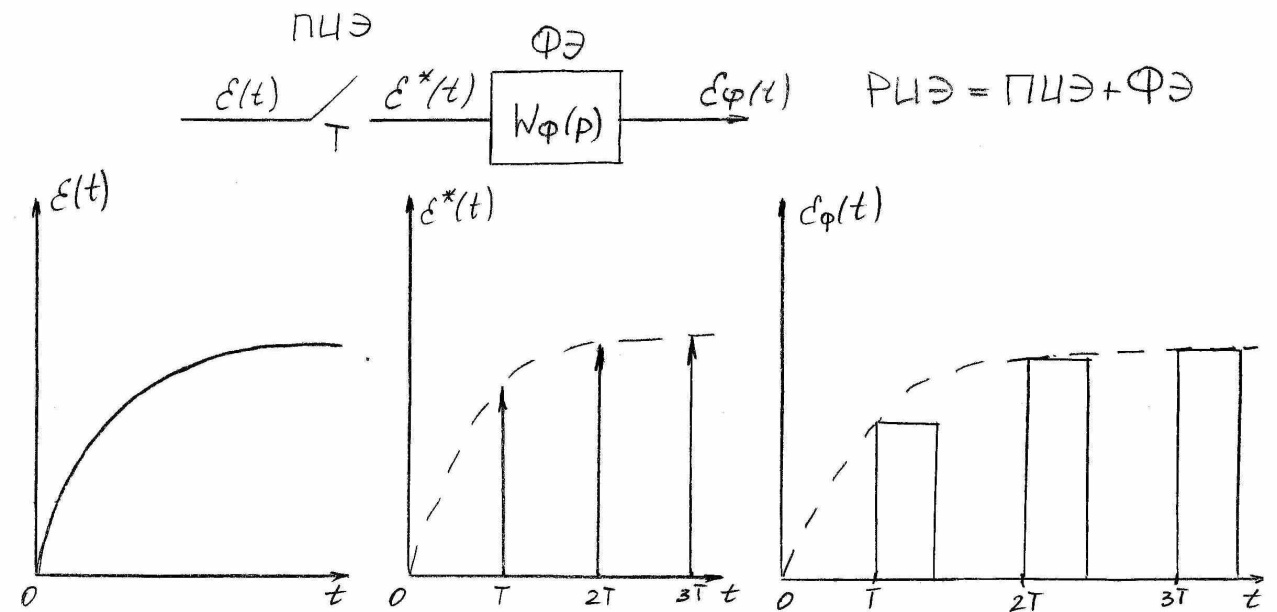
Рисунок 1.
Такую
замену выполняют, осуществляя следующие
условия: при одинаковых входных сигналах
![]() выходные сигналы РИЭ и математической
модели должны быть одинаковы. Математическая
модель РИЭ идеальна и не может быть
реализована такими техническими
средствами. Операция замены РИЭ мат.
Моделью является только математическим
приемом, позволяющим упростить
математический аппарат исследования
амплитудно-импульсных систем.
выходные сигналы РИЭ и математической
модели должны быть одинаковы. Математическая
модель РИЭ идеальна и не может быть
реализована такими техническими
средствами. Операция замены РИЭ мат.
Моделью является только математическим
приемом, позволяющим упростить
математический аппарат исследования
амплитудно-импульсных систем.
Простейший импульсный аппарат ПИЭ представляет собой обычный прерыватель (ключ) с периодом дискретности Т и преобразует непрерывный входной сигнал
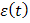 в
кратковременные импульсы
в
кратковременные импульсы 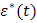 ,
площадь которого пропорциональна
значению входного сигнала в дискретные
моменты времени.
,
площадь которого пропорциональна
значению входного сигнала в дискретные
моменты времени.
Работу такого элемента можно представить следующим образом: некоторый внутренний источник сигналов содержащийся в ПИЭ (рисунок 2а) генерирует бесконечную последовательность импульсов типа -функции, каждый из которых существует только в дискретный момент времени: 0, Т, 2Т,… (рисунок 2б)
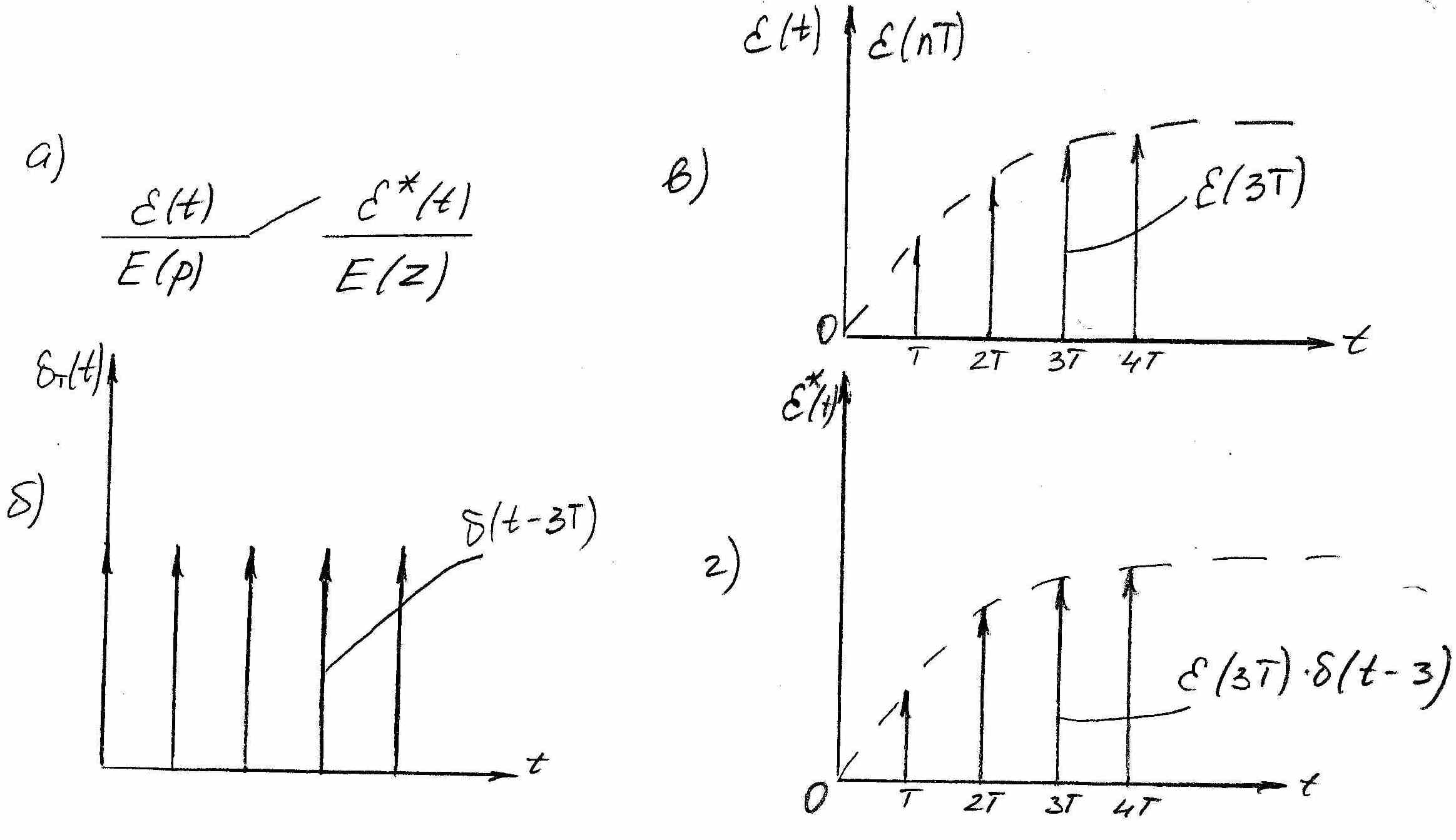
Рисунок 2
Такой сигнал можно представить в виде суммы смещенных -импульсов:
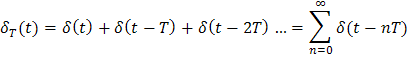
Эта запись
означает следующее. Поскольку аргументом
в этой формуле является время t,
то каждый импульс типа![]() -функции
возникает в дискретный момент времени:
0, Т, 2Т,…,nT
и существует только в этот указанный
момент времени. Во
все остальные моменты времени, неравные
данному, импульс отсутствует (сигнал
типа -функции равен 0). Совокупность
полученных таким образом импульсных
сигналов записана в формуле в виде суммы
смещенных -функций. В
ПИЭ происходит умножение последовательности
-функций на непрерывный входной сигнал
(рисунок 2в). В
результате на выходе ПИЭ имеет место
сигнал следующего вида:
-функции
возникает в дискретный момент времени:
0, Т, 2Т,…,nT
и существует только в этот указанный
момент времени. Во
все остальные моменты времени, неравные
данному, импульс отсутствует (сигнал
типа -функции равен 0). Совокупность
полученных таким образом импульсных
сигналов записана в формуле в виде суммы
смещенных -функций. В
ПИЭ происходит умножение последовательности
-функций на непрерывный входной сигнал
(рисунок 2в). В
результате на выходе ПИЭ имеет место
сигнал следующего вида:
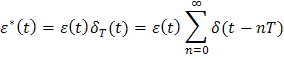
Учитывая, что суммирование производится по параметру n, выходной сигнал ПИЭ можно представить в форме:
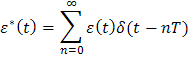
Поскольку
каждое слагаемое этой суммы отлично от
0 только в дискретные моменты времени
nT
(во все остальные моменты ![]() эти слагаемые равны
нолю), целесообразно в функции
эти слагаемые равны
нолю), целесообразно в функции
![]() непрерывный аргумент
непрерывный аргумент
![]() заменить на дискретный nT.
В результате последнее выражение
принимает вид:
заменить на дискретный nT.
В результате последнее выражение
принимает вид:
![]()
Каждое слагаемое в этом
выражении можно трактовать как
![]() -
импульс, площадь которого изменена в
-
импульс, площадь которого изменена в
![]() раз. Только в этом существует формальное
различие между функциями
раз. Только в этом существует формальное
различие между функциями
![]() и
(рис 2(в))
и
(рис 2(в))
Условно сигнал изображён на рис 2(г) в виде стрелок различной длины. Каждая стрелка образуется как произведение импульсного сигнала типа - функции, возникающего в дискретный момент времени nT на значение входного сигнала в дискретный момент времени nT.
Поскольку операции умножения соответствует модулирование(изменение) сигналов, то ПИЭ можно рассматривать как импульсный модулятор, осуществляющий модулирование по площади последовательности - импульсов(рис 3)
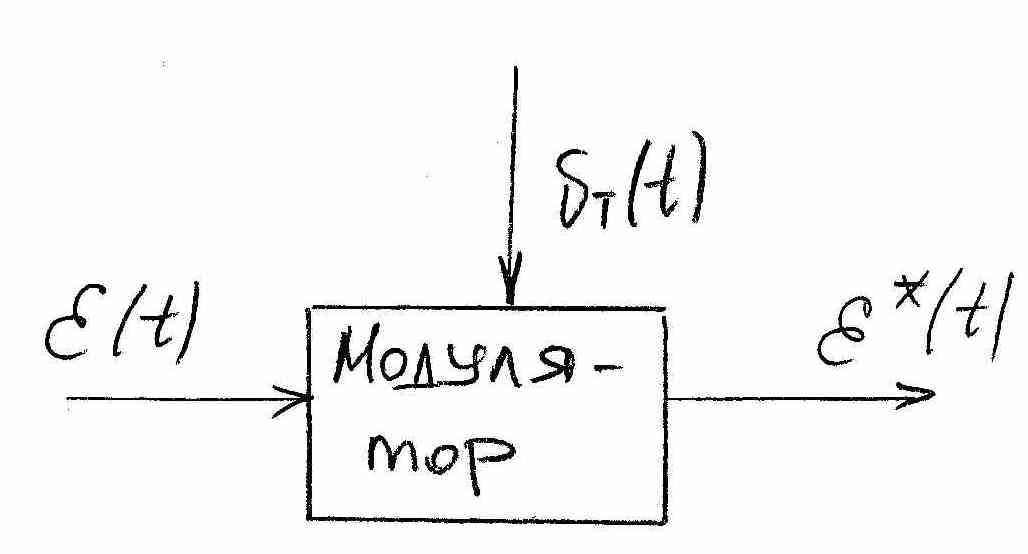
Рисунок 3
Причём в качестве модулирующего сигнала в таком устройстве используется непрерывный входной сигнал .
Итак, сигнал на выходе ПИЭ представляет собой моделированную последовательность импульсов типа - функций возникающих в дискретный момент времени nT, площади которых равны значениям непрерывного входного сигнала в соответствующие дискретные моменты времени nT. Для уяснения последующего материала следует отметить, что обычное преобразование Лапласа сигнала совпадает с Z – преобразованием решётчатой функции входного сигнала ПИЭ. Действительно подвергнем выходной сигнал ПИЭ обычному преобразованию Лапласа:
![]()
Учитывая, что по теореме
сдвига
![]() будем иметь:
будем иметь:
![]()
Это выражение свидетельствует
о том, что обычное изображение Лапласа
выходного сигнала ПИЭ
совпадает с дискретным изображением
решетчатой функции входного сигнала
данного элемента. Заменяя
![]() получаем:
получаем:
![]()
Таким образом обычное изображение Лапласа выходного сигнала ПИЭ совпадает с Z – изображением дискретной функции входного сигнала.
Рассмотрим полученные математические зависимости в частотной области. Для этого воспользуемся рядом Фурье записанным в комплексной форме. Тогда немодулированную последовательность - импульсов можно представить в виде суммы гармоник(рис 4(а))
![]()
![]() - угловая частота следования импульсов
- угловая частота следования импульсов
![]()
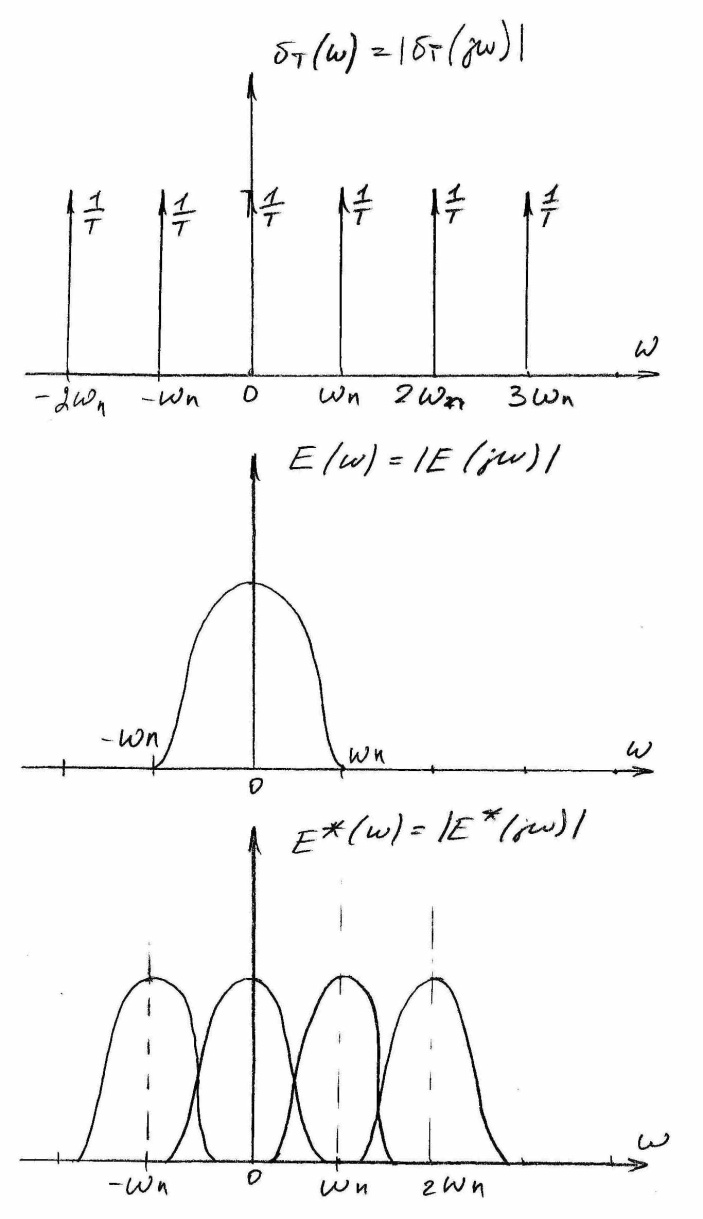
Рисунок 4
![]()
![]()
В этом случае выходной сигнал ПИЭ будет представлен в следующем виде
![]()
Умножая обе части равенства
на
![]() и выполняя интегрирование в интервале
от 0 до
получим:
и выполняя интегрирование в интервале
от 0 до
получим:
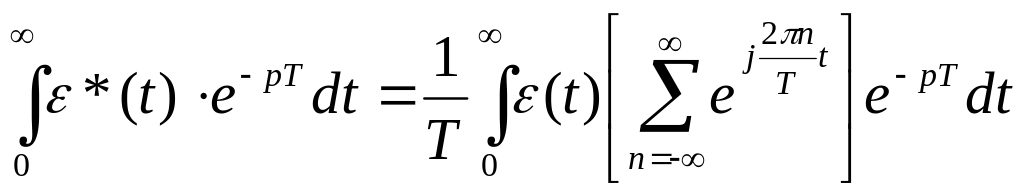
Откуда следует
![]()
Таким образом дискретный
сигнал
![]() представляет собой бесконечное число
входных сигналов. На рисунке 4(б)
представлена амплитудная
характеристика(амплитудный спектр)
входного непрерывного сигнала. Тогда
подставляя в последнее выражение
представляет собой бесконечное число
входных сигналов. На рисунке 4(б)
представлена амплитудная
характеристика(амплитудный спектр)
входного непрерывного сигнала. Тогда
подставляя в последнее выражение
![]() получим:
получим:
![]()
Из этого выражения видно, что
амплитудный спектр дискретного сигнала
представляет собой бесконечную сумму
спектров входного сигнала
,
смещённых вдоль оси абсцисс на величины
![]() .
.
2) Формирующий элемент.
ФЭ является непрерывным
линейным устройством(звеном), которое
формирует выходной импульсный сигнал
![]() совершенно идентичный по своим параметрам
и форме сигналу на выходе РИЭ. Естественно,
что для этого ПФ-ия формирующего элемента
совершенно идентичный по своим параметрам
и форме сигналу на выходе РИЭ. Естественно,
что для этого ПФ-ия формирующего элемента
![]() должна быть подобрана таким образом,
чтобы реакция указанного элемента на
модулированный
-
импульс представляла собой точно такой
же импульс, как и на выходе РИЭ.
должна быть подобрана таким образом,
чтобы реакция указанного элемента на
модулированный
-
импульс представляла собой точно такой
же импульс, как и на выходе РИЭ.
Определим ПФ-ию ФЭ
в соответствии с принятой математической
моделью РИЭ. При этом будем полагать,
что в момент времени
![]() на вход ФЭ воздействует импульс
на вход ФЭ воздействует импульс
![]() (рис 5(а)).
(рис 5(а)).
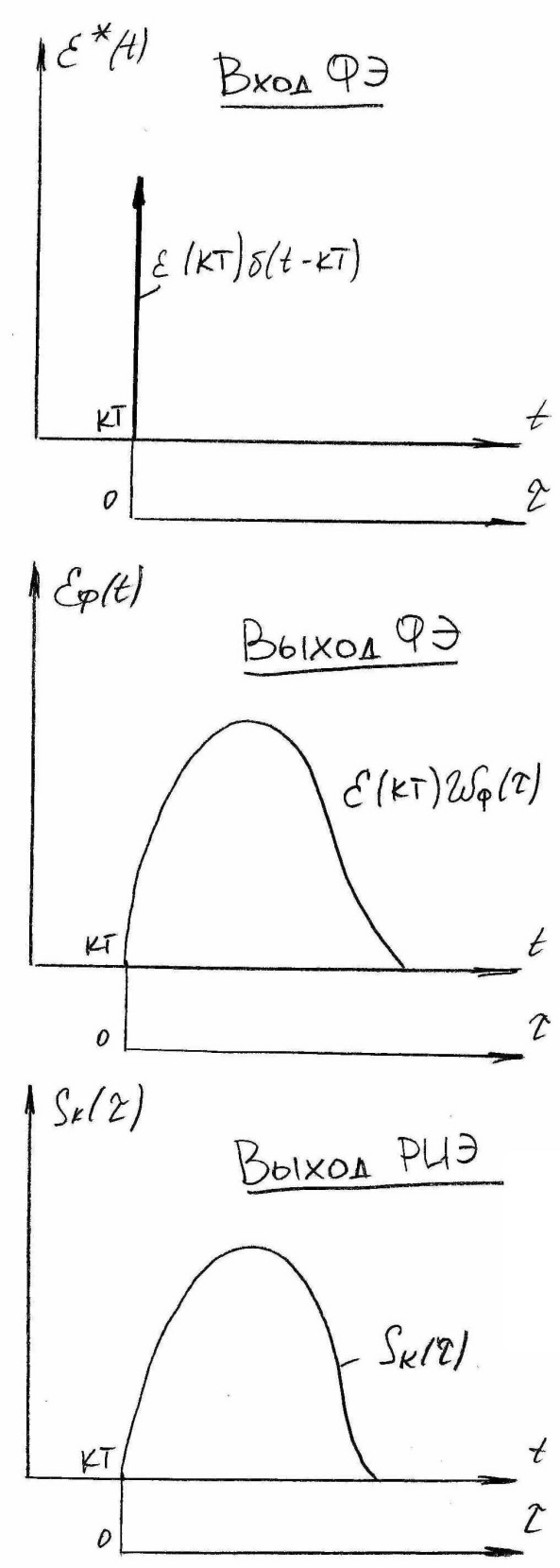
Рисунок 5
На рисунке начало отсчёта
переменной
совмещено с моментом времени
,
то есть
![]() .
Известно, что реакция линейного
непрерывного звена на импульсный сигнал
типа
-
функции есть весовая функция
.
Известно, что реакция линейного
непрерывного звена на импульсный сигнал
типа
-
функции есть весовая функция
![]() данного звена. Поэтому реакцию ФЭ
на импульс
данного звена. Поэтому реакцию ФЭ
на импульс
![]() можно представить(рис 5(б)) следующей
формулой:
можно представить(рис 5(б)) следующей
формулой:
![]() ,
,
где
![]() - весовая функция.
- весовая функция.
Пусть k-й импульс
на выходе РИЭ (рис 5(в)) описывается
функцией формы
![]() .
Учитывая изложенное выше требование
к динамическим свойствам ФЭ, потребуем
выполнение равенства:
.
Учитывая изложенное выше требование
к динамическим свойствам ФЭ, потребуем
выполнение равенства:
![]()
Отсюда получаем условие, которому должна соответствовать весовая функция формир. ФЭ:
![]()
Последнее равенство позволяет определить ПФ-ию ФЭ:
![]()
Таким образом, чтобы определить необходимо, выполнить следующее:
- любой импульс РИЭ аппроксимировать аналитической функцией ;
- уменьшить ординаты этой
функции в
![]() ,
где
-
значение непрерывного входного сигнала
в рассматриваемый момент времени
;
,
где
-
значение непрерывного входного сигнала
в рассматриваемый момент времени
;
- подвергнуть полученный в предыдущем пункте результат преобразования Лапласа.
Определим
,
если РИЭ формирует на выходе импульсы
прямоугольной формы длительностью
![]() (рис 6).
(рис 6).
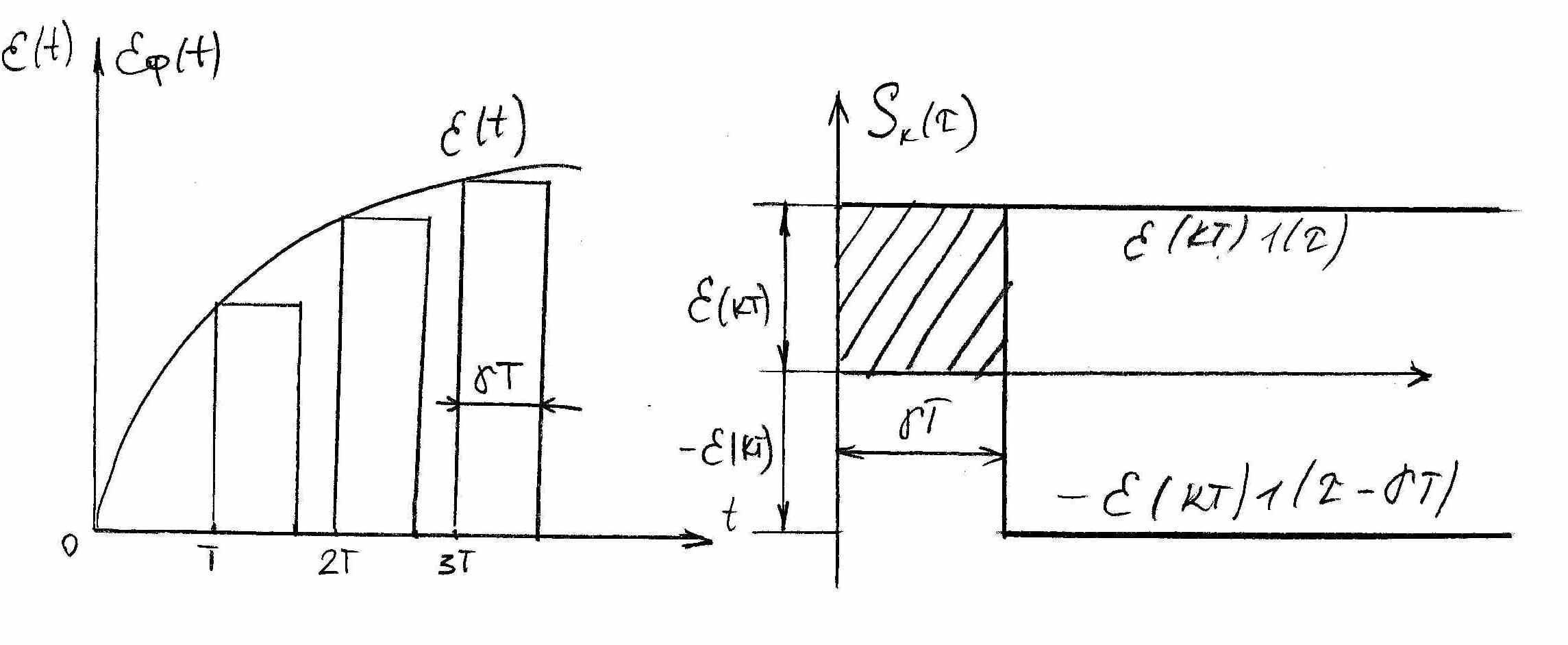
Рисунок 6
Произвольный К-й импульс с
РИЭ (рис. 6(б)) аппроксимируем суммой двух
ступенчатых функций, сдвинутых во
времени на
![]() Т
и имеющие различные знаки.
Т
и имеющие различные знаки.
![]() .
.
Уменьшаем ординаты функции
![]() в
раз, определяем весовую функцию ФЭ:
в
раз, определяем весовую функцию ФЭ:
![]() .
.
ПФ-я ФЭ:
![]() .
.
Обычно коэффициент передачи
РИЭ
![]() относят к ФЭ, считая, что коэффициент
передачи ПИЭ равен 1. В связи с этим
ПФ-я ФЭ:
относят к ФЭ, считая, что коэффициент
передачи ПИЭ равен 1. В связи с этим
ПФ-я ФЭ:
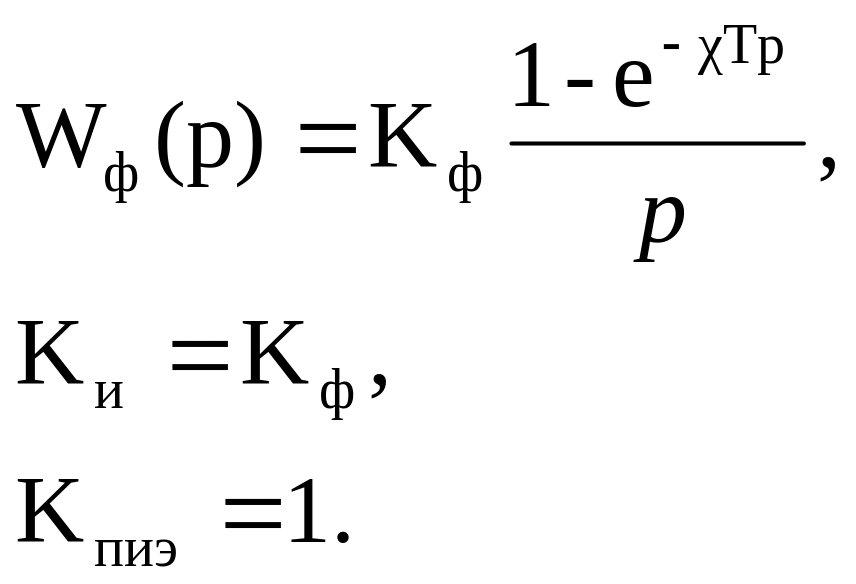
РИЭ называют фиксатором, если он формирует прямоугольные импульсы, длительность которых равна периоду длительности Т, т. е. РИЭ является фиксатором, если =1. В этом случае ПФ-я фиксатора имеет вид:
![]() . (4)
. (4)
Реакция фиксатора
![]() на последовательность модулированных
по площади
-импульсов
на последовательность модулированных
по площади
-импульсов
![]() показана на рисунке 7. Как видно из
рисунка фиксатор запоминает (фиксирует)
величину площади каждого
-импульса
на период дискретности Т, т. е. до прихода
следующего импульса. Во многих практических
случаях, где необходимо преобразование
дискретных данных в непрерывные, на
выходе РИЭ перед непрерывной частью
системы включают фиксатор, поскольку
он позволяет приближенно решать задачу
преобразования импульсного сигнала
в
непрерывный
показана на рисунке 7. Как видно из
рисунка фиксатор запоминает (фиксирует)
величину площади каждого
-импульса
на период дискретности Т, т. е. до прихода
следующего импульса. Во многих практических
случаях, где необходимо преобразование
дискретных данных в непрерывные, на
выходе РИЭ перед непрерывной частью
системы включают фиксатор, поскольку
он позволяет приближенно решать задачу
преобразования импульсного сигнала
в
непрерывный
![]() .
.
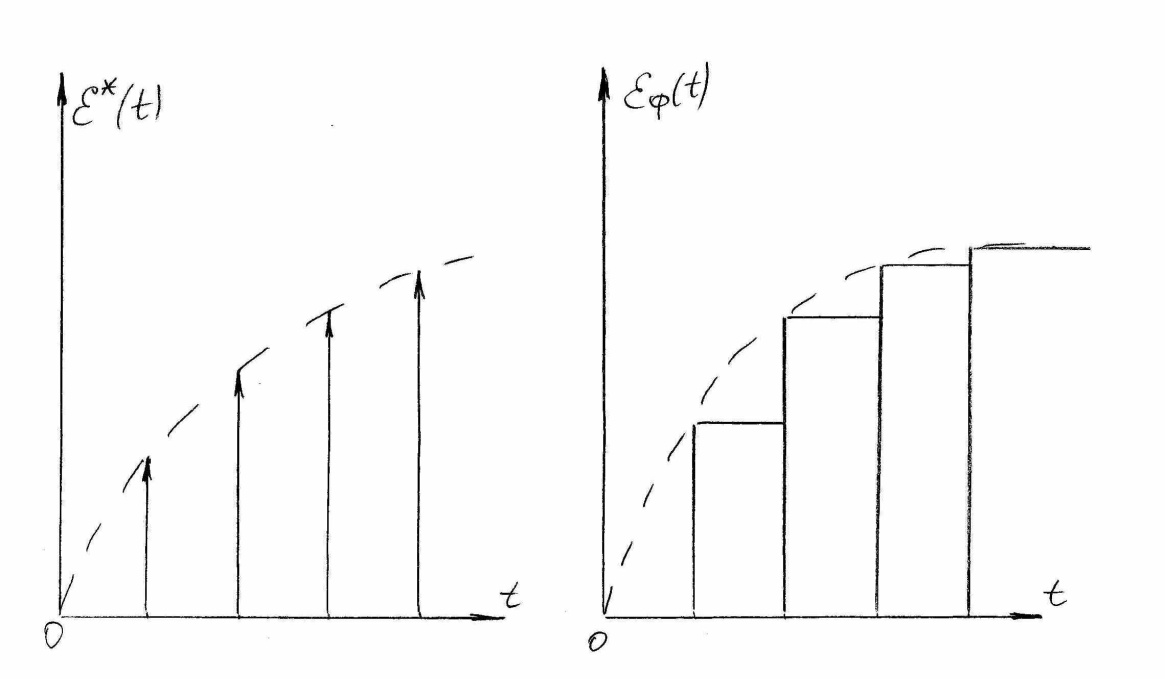
Рисунок 7
Для того, чтобы качественно оценить влияние эффекта квантования сигнала по динамику импульсной системы САР, рассмотрим частотные свойства фиксатора. Частотная ПФ-я в соответствии с уравнением (4) запишется в виде:
![]() ,
,
или в показательной форме:
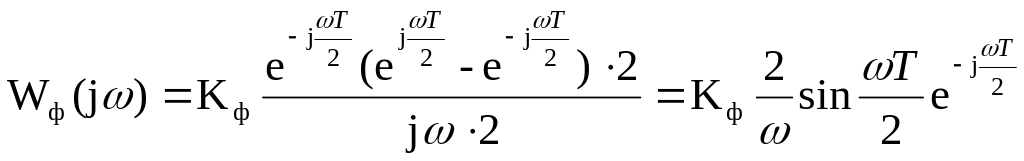 ,
,
откуда АЧХ фиксатора:
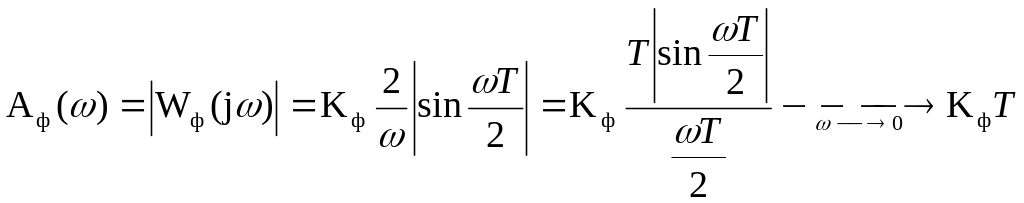 ,
,
а ФЧХ:
![]() .
.
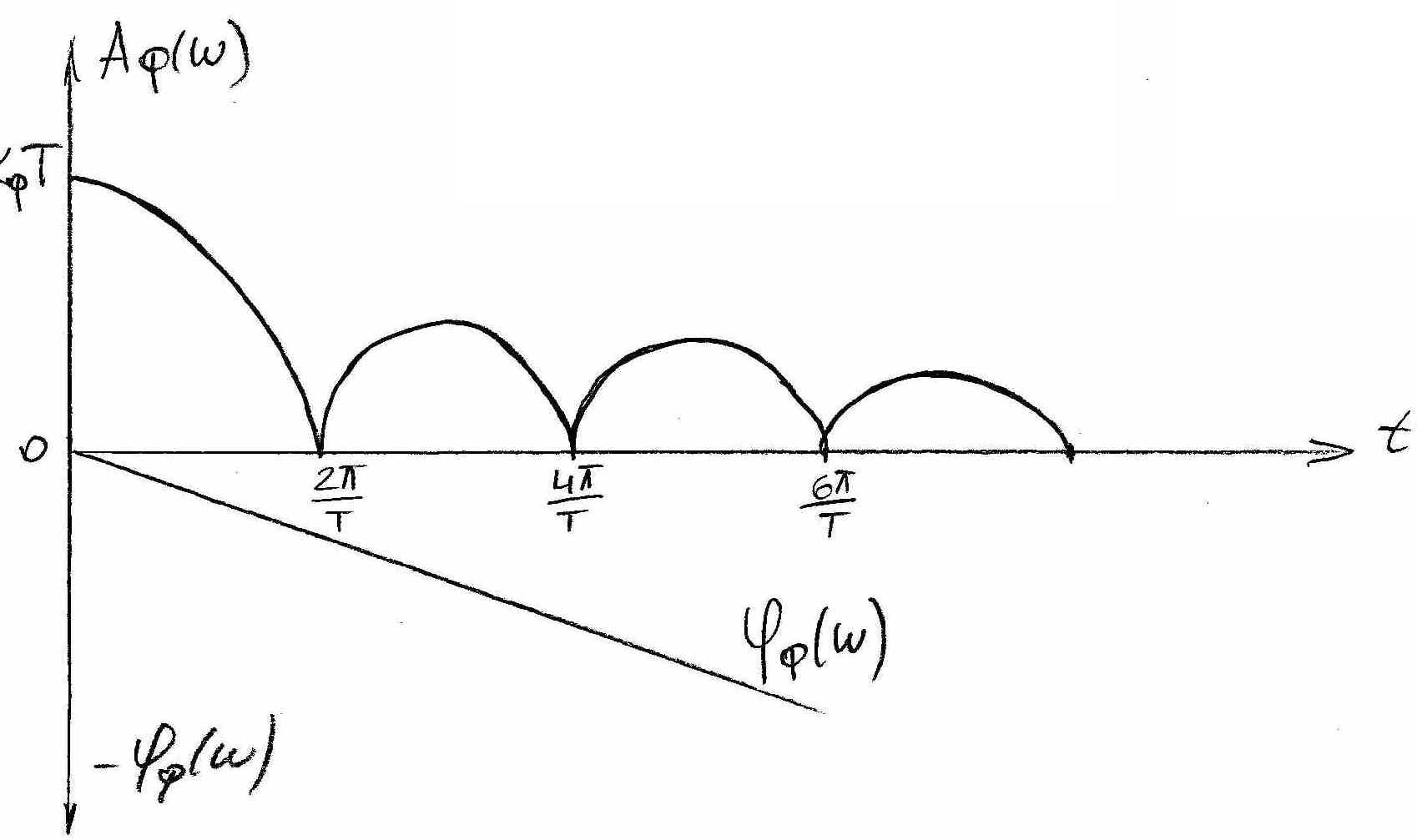
Рисунок 8
Как видно из рисунка 8 фиксатор представляет собой фильтр низких частот, при этом, чем больше период дискретности Т, тем уже полоса пропускания и больше по абсолютной величине отрицательный фазовый сдвиг на всех частотах. Т. о. выбор большой величины Т может привести не только к существенному искажению сигналов в системе, но и к потери устойчивости в системе. Отсюда важной становится проблема выбора дискретной величины Т.
