3.6.* Общий случай движения свободного твердого тела

Чтобы в общем случае определить положение свобод-ного твердого тела в пространстве относительно непод-вижной системы координат Охуz, свяжем с произвольной точкой А тела, в дальнейшем называемой полюсом, подвижную систему координат Ах₁у₁z_1, которая переме-щается поступательно и оси которой остаются параллель-ными осям неподвижной системы координат Охуz. Положение подвижной системы относительно неподвиж-ной определяется положением ее начала, полюса А, то есть тремя координатами: х_А, у_А, z_А. Относительно подви-жной системы Ах₁у₁z₁ тело совершает сферическое движение (в этой системе точка А неподвижна), и его относительное движение определяется тремя углами Эйлера. Таким образом, шесть равенств

(3.47)

определяющих положение полюса А и положение тела относительно подвижной системы координат полностью задают положение тела относительно неподвижной системы координат в каждый момент времени. Поэтому эти равенства называются уравнениями движения свободного твердого тела.

Если бы в процессе движения углы ψ, θ и φ остава-лись неизменными, то тело перемещалось бы поступа-тельно в соответствии с тремя первыми уравнениями системы (3.47). Если бы полюс А тела оставался непод-вижным, то тело двигалось бы вокруг неподвижной точ-ки А согласно трем последним уравнениям системы (3.47). В действительности же в общем случае движения твердого тела меняется как положение полюса, так и углы Эйлера. Поэтому мы можем сказать, что в общем случае движение твердого тела в каждый момент време-ни слагается из поступательного движения, при котором все точки движутся со скоростями произвольно выб-ранного полюса А, и из вращения с мгновенной угловой скоростью вокруг мгновенной оси вращения, прохо-дящей через полюс А.

Для радиуса вектора произвольной точки В относите-льно неподвижной точки О в каждый момент времени справедлива зависимость (рис. 3.39)

,

где - радиус-вектор полюса А, а - постоянный по модулю радиус-вектор точки В относительно полюса А.

П родифференцировав это равенство по времени, полу-чим .

Здесь - ско-рость точки В, - скорость полюса А,

-

Рис. 3.39 скорость точки В тела при его вращении вокруг мгновенной оси.

Таким образом, мы получили формулу, определяющую скорость произвольной точки В в общем случае движения твердого тела:

. (3.48)

Примеры движения свободного твердого тела: брошенный камень, самолет, проделывающий фигуры высшего пилотажа, артиллерийский снаряд, и т.д.

3.7. Сложное движение точки

3.7.1. Относительное, переносное и абсолютное движения точки

Сложное (составное) движение точки – такое движение, при котором точка одновременно участвует в двух или нескольких видах движения. Например, пассажир, перемещающийся в вагоне движущегося поезда или на палубе плывущего корабля по отношению к условно неподвижной системе отсчета, связанной с землей, совершает сложное движение.

Рассмотрим движущееся тело А и точку М, не при-надлежащую этому телу, а совершающую по отношению к нему некоторое движение (рис. 3.40). Выберем две сис темы координат: неподвижную систему координат О₁х₁y₁z₁ в условно неподвижной системе отсчета и систему координат Охуz, которая проведена через некоторую точку тела О и жестко с ним связана. Систему Охуz называют подвижной системой координат.

Движение точки М по отношению к неподвижной системе координат называется абсолютным и определя-ется радиус-вектором , а ее скорость и ускоре-ние соответственно называются абсолютной скоро-стью и абсолютным ускорением.

Д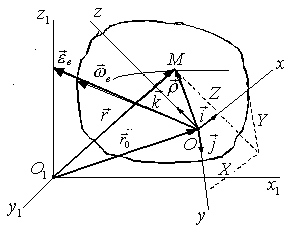 вижение точки М по отношению к подвижной системе координат Охуz называется относительным движением и определяется радиус-вектором , а ее скорость и ускорение соответст-венно называются отно-сительной скоростью и относительным уско-рением.

Движение подвижной системы координат отно-сительно неподвижной

Рис. 3.40 называется переносным. Точки тела А, связанного с подвижной системой отсчета, имеют различные скорости и ускорения, в зависимости от вида движения твердого тела (см. п. 3).

Движение точки О подвижной системы координат относительно точки О₁ неподвижной системы определя-ется радиус–вектором . Скорость и ускорение точки тела, с которой в данный момент времени совпадает движущаяся точка, называются переносной скоростью ( ) и переносным ускорением ( ). Например, в случае движения человека по эскалатору метро переносной ско-ростью человека будет скорость ступеньки, на которой он в данный момент находится.

Положение точки М относительно подвижной систе-мы отсчета (рис. 3.40) определяется радиусом вектором

, (3.49)

проведенным из начала этой системы О в точке М или тремя координатами x,y,z , которые являются функциями времени t

, (3.50)

и называются уравнениями относительного движения точки.

Положение точки М по отношению к неподвижной системе отсчета можно определить радиус-вектором

, (3.51)

Основной задачей при изучении сложного движения точки является установление зависимостей между скоростями и ускорениями абсолютного, относительного и переносного движений.