3.4.9. Мгновенный центр ускорений

При непоступательном движении твердого тела в его сечении (S) в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений (МЦУ).

Определяется положение центра Q, если известно ускорение какой-нибудь точки тела и величины , следующим образом:

1. вычисляем величину угла по формуле ,

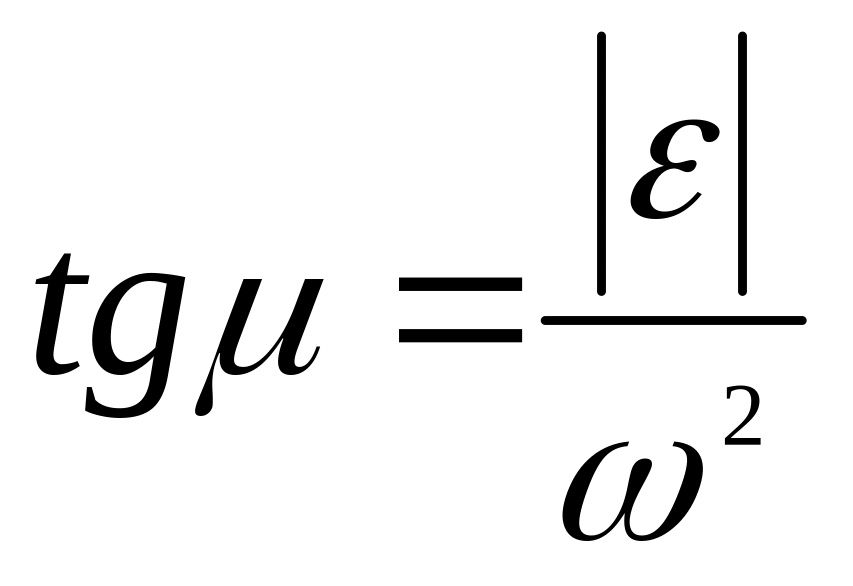2. от точки А под углом к вектору проводим пря-мую АЕ (рис. 3.32); при этом прямая должна быть откло-нена от в сторону вращения, если вращение ускорен-ное и против вращения, если оно замедленное,

3. откладываем вдоль линии АЕ отрезок AQ, равный

. (3.40)

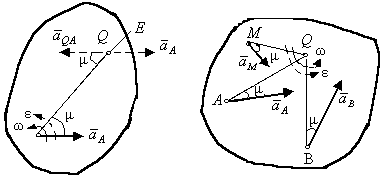
Рис. 3.32 Рис. 3.33

Построенная таким путем точка Q и будет мгновенным центром ускорений (МЦУ). В самом деле, по формулам (3.37) и (3.38) заключаем, что

• ускорение любой точки тела равно ее ускорению во вращательном движении вокруг МЦУ, а

, (3.41)

• при этом

, (3.42 )

то есть ускорения точек тела пропорциональны их расстояниям до МЦУ (рис. 3.33)

• М ЦУ и МЦС – являются различными точками сечения (S) фигуры. Например, колесо катится без скольжения по прямолинейному пути (рис. 3.34), причем скорость его центра постоянна ( ). Тогда мгновенный центр скоростей колеса находится в точке Р (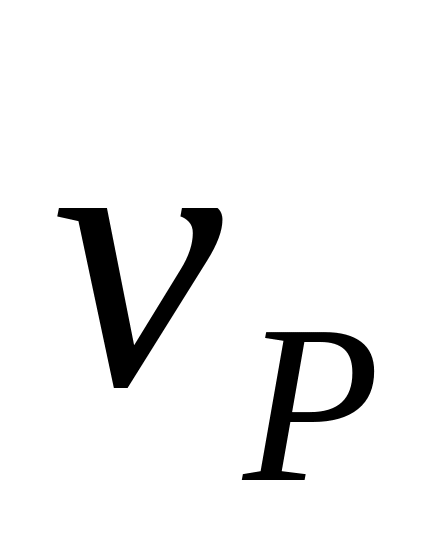 = 0) – в точке касания с землей. Мгновенный центр ускорений в этом случае, очевидно, находится в точке С, так как она движется равномерно и прямоли-нейно и . Центры скоростей и ускорения совпада-ют тогда, когда тело вращается вокруг неподвижной оси.

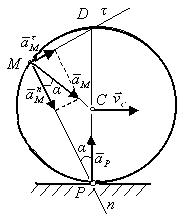
Пример. Колесо катится по прямолинейному рельсу так, что скорость его центра постоянна . Определить ускорение точки М обода колеса (рис. 3.34).

Решение. Так как точка С, как показано выше, в данном случае

Рис. 3.34 является мгновенным центром

ускорений – МЦУ, а мгновенный центр скоростей находится в точке Р, то для колеса

По формуле (3.41) находим . Следовательно, ускорения любой точки обода колеса (в том числе и точки Р) равны и направлены к центру С колеса, так как угол μ = 0. Но ускорение точки М не будет нормальным ускорением. Так как скорость точки М направлена перпендикулярно РМ, то касательная Мτ к траектории точки М направлена вдоль МD, а главная нормаль Мп – вдоль МР. Поэтому .

3.4.10. План ускорений и его свойства

Планом ускорений звена плоского механизма назы-вается графическое построение, представляющее собой плоский пучок, лучи которого изображают абсолютные ускорения точек звена, а отрезки, соединяющие концы лучей, изображают относительные ускорения соответ-ствующих точек в данном положении звена. Совокуп-ность планов ускорений звеньев с одним общим полюсом и одним масштабом называется планом ускорения механизма.

Основные свойства плана ускорений:

1. векторы абсолютных ускорений точек фигуры выходят из полюса плана ускорений;

2. векторы относительных ускорений точек фигуры изображаются отрезками, соединяющими концы векто-ров абсолютных ускорений;

3. фигура на плане ускорений (отрезок, прямоуголь-ник, многоугольник и др.), образуемая относительными ускорениями, подобна одноименной фигуре на движу-щемся неизменяемом теле и повернута относительно последнего на угол (180°-µ) по направлению углового ускорения вращения тела;

4. порядок букв при обходе по контурам одноимен-ных фигур, как на плане ускорений, так и на неизменяе-мой фигуре, одинаковый. При этом обход надо начинать от одной и той же буквы и производить в одном и том же направлении, как на плане ускорений, так и неизменяе-мой фигуре.

Рассмотрим пример построения плана ускорений. Определим ускорения точек В, С и D фигуры АВС (рис. 3.35, а), если известны ускорение точки А и линия действия ускорения точки В.

Построим фигуру АВС (рис. 3.35, а) в выбранном масштабе длин λ_L. Определим ускорение точки В, прове-дя графическое решение уравнения, выражающего тео-рему о сложении ускорений точки тела, совершающего плоскопараллельное движение

. (3.43)

То есть, вектор ускорения , точки В фигуры, совер-шающей плоскопараллельное движение, равен геометри-ческой сумме векторов: ускорения точки А, принятой за полюс, и ускорения от вращения точки В вместе с телом вокруг полюса А.

Здесь и далее вектор, известный по величине и направлению, подчеркнут двумя линиями, а вектор, известный по величине или направлению, подчеркнут одной линией, под которой указано это направление.

Решим графически уравнение (3.43) с помощью пла-на ускорений при условии, что линия действия вектора ускорения точки В известна. Для этого из произвольно выбранного полюса π (рис. 3.35, б) отложим в выбранном масштабе ускорений λ_а вектор , изображающий уско-рение . К концу этого вектора (к точке а) согласно уравнению (3.43) прикладываем вектор, изображающий ускорение в том же масштабе. Модуль вектора равен , а угловая скорость ω_АВ, уже определена планом скоростей (см. пример п. 3.4.6).

К концу п этого вектора прикладываем вектор каса-тельного ускорения . Так как модуль этого вектора не известен, то через точку п проводим только линию дей-ствия этого вектора (линию, перпендикулярную к АВ на фигуре АВС). А через полюс π проведем линию действия вектора . Точку пересечения линий действия назван-ных векторов обозначим буквой b. После этого соеди-ним точки а и b, а так же полюс π с точкой b. Вектор и будет изображать ускорение точки В. Направлен вектор нормального ускорения по АВ от точки В к точке А.

Ускорение точки С определим с помощью свойства подобия фигур тела и плана ускорений. Для этого на стороне аb плана ускорений строим треугольник аbс, подобный треугольнику АВС, и в таком же положении, чтобы обход по контурам этих треугольников был в одном направлении (рис. 3.35, в). Для построения треугольника аbс, подобного АВС, использовано равен-ство углов. Соединив полюс π с точкой с, получим век-тор , который и будет изображать ускорение точки С.

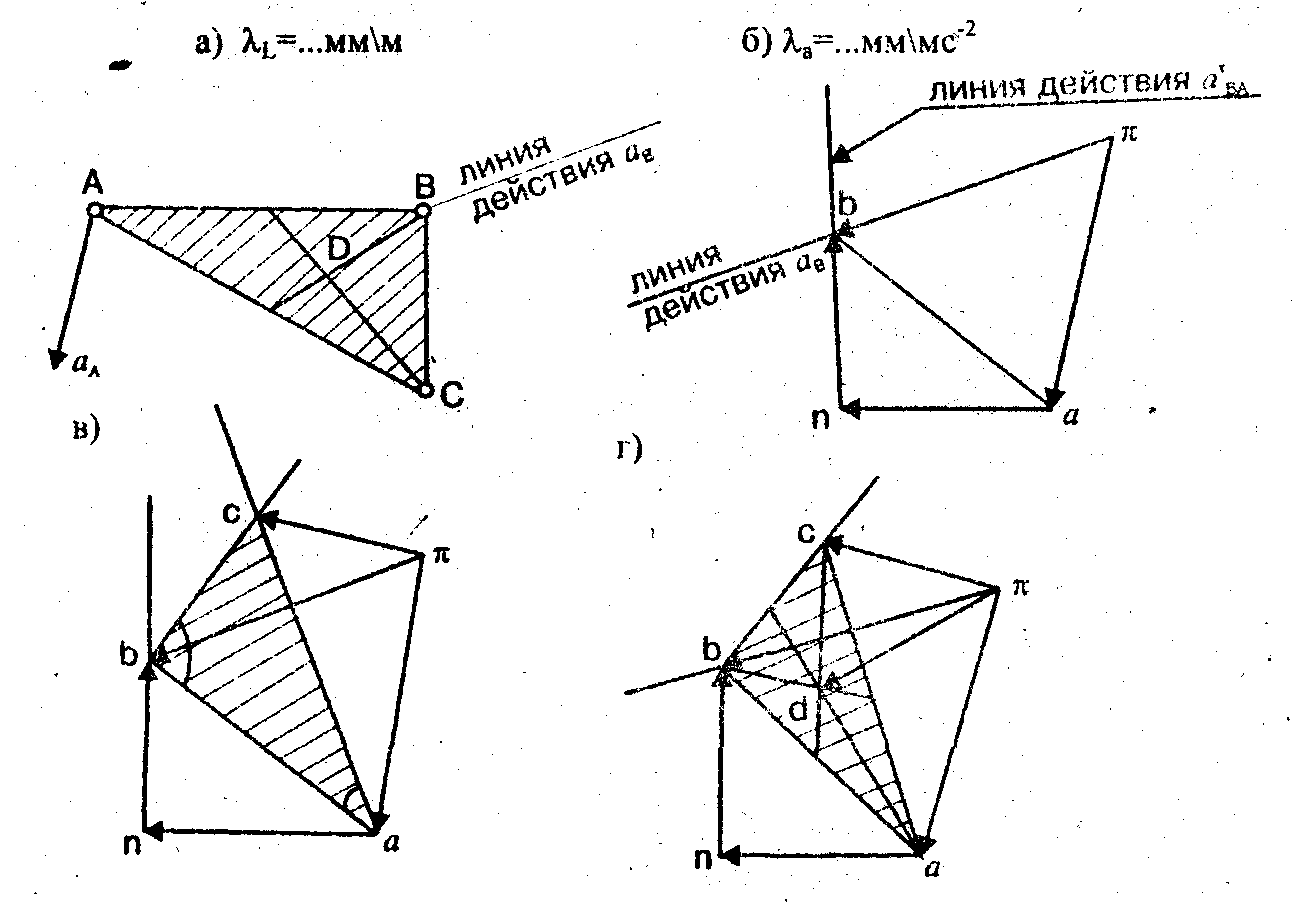
Рис. 3.35. Определение ускорений точек фигуры АВС

а) фигура АВС; б) определение ускорения точки В;

в) определение ускорения точки С; г) определение ускорения точки Д

Определим ускорение точки D, с помощью свойства подобия. Точка D лежит на пересечении медиан треу-гольника АВС (рис. 3.35, а). Следовательно, в одно-именном треугольнике abc плана ускорений точка d лежит также на пересечении медиан последнего. Прове-дем медианы треугольника аbc (рис. 3.35, г). Соединим полюс π с точкой d пересечения медиан, получим вектор , который и будет изображать ускорение точки D.

С помощью вектора можно определить значение и направление углового ускорения ε плоской фигуры

или ,

где πb – отрезок, взятый с плана ускорений, λ_a – масштаб ускорений.

При определении направления углового ускорения, вектор , изображающий слагаемое в уравнении (3.43), мысленно перенесем с плана ускорений параллельно самому себе в точку В на плоской фигуре. Тогда видно, что угловое ускорение ε направлено против хода часовой стрелки при вращении фигуры вокруг полюса А.

Пример. Определить ускорения точек А, В, С, D и угловые ускорения звеньев механизма для положения, изображенного на чертеже (рис. 3.36, а), если кривошип ОА вращается с постоянной угловой скоростью ω₁. Кривошип О₁В соединен шарниром с серединой шатуна АС.

Решение: 1) Выбрав масштаб длин λ_L=…мм/м. (например, если 1 мм чертежа фигуры содержит 0,1 м длины реальной фигуры, то λ_L=10 мм/м), изображаем механизм в данном положении (рис. 3.36, а).

2) Определение скоростей точек А, В, С и D. Определим скорость точки А по величине и направлению. Так как криво-шип вращается вокруг неподвижной оси, проходящей через неподвижную точку О, то модуль скорости точки А равен v_А=ω₁ОА и направлен вектор скорости перпендикулярно ОА в сторону направления угловой скорости ω₁. Построим план скоростей (см. пример п. 3.4.6) в выбранном масштабе по скорости λ_v=…мм/мс^-1 (например, если один мм плана скоростей содержит скорость 0,5 м/с, то λ_v=2мм/мс^-1). Измерим на плане скоростей (рис. 3.36, б) отрезки Оb, Ос, Оd , аb и определим модули скоростей точек В, С, D, угловую скорость ω₂ тела АВСD и угловую скорость ω₃ звена О₁В по формулам:

, , ,

, .

3) Определение . При вращательном движении твердо-го тела вокруг неподвижной оси ускорение точки А равно

Р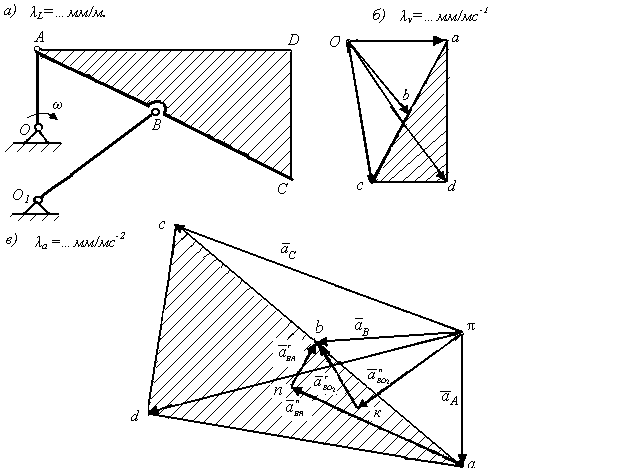 ис. 3.36

. Так как кривошип ОА вращается с постоян-ной угловой скоростью ω₁, то ускорение = 0, а ускорение точки А будет равно только нормальной составляющей уско-рения . Определим величину ускорения точки А по формуле . Выбрав масштаб ускорений λ_а= … мм/мс^-2 (например, 1 мм плана ускорений содержит 10 м/с^-2, то λ_а =0,1 мм/мс^-2), отложим в этом масштабе от некоторого центра π вектор , направленный по ОА от точки А.

4. Определение . Точка В механизма принадлежит зве-ну АВСD, совершающему плоскопараллельное движение. Следовательно, по теореме о сложении ускорений (3.43), если за полюс взять точку А, ускорение которой известно, ускорение точки В будет равно

.

С другой стороны точка В так же принадлежит звену О₁В, которое совершает вращательное движение вокруг неподвижной оси, проходящей через точку О₁, а ускорение точки В соответственно будет равно

.

Приравнивая правые части полученных выражений, имеем

= .

Выразим это равенство графически. К вектору от точки а на плане ускорений откладываем в выбранном масш-табе вектор = ( ║ ВА и направлен от точки В к точ-ке А) и от точки п проводим прямую пb, перпендикулярную ап. Эта прямая дает направление и где-то на ней должен лежать конец искомого вектора .

Теперь от точки π откладываем вектор = ( ||ВО₁) и проводим перпендикулярную к нему прямую κb, дающую направление . Конец вектора должен лежать и на этой прямой. Следовательно, точка b пересечения линий пb и κb и дает конец вектора . Таким образом = . Измерив длину πb и учитывая масштаб, найдем в нашем случае, что . Одновременно из построения следует, что и .

5) Определение угловых ускорений звеньев. Измерив длины отрезков пb и κb найдем угловые ускорения звеньев по формулам

и .

Из планов скоростей и ускорений видим, что векторы скорости точки В и ускорения направлены в проти-воположные стороны. Следовательно, звено О₁В движется замедленно. Сравнивая направления векторов скорости и ускорения , видим, что они тоже направлены в противоположные стороны. Следовательно звено АВСD тоже движется замедленно.

6) Определение . Используя свойство подобия фигур АВС на механизме и авс плане ускорений определим положе-ние точки с на плане ускорений из условия пропорциональ-ности

.

Отложим от точки b отрезок . Тогда, соеди-нив точку с с центром плана ускорений π, получим ускорение . Модуль ускорения точки С определим с учетом масштаба ускорения, измерив отрезок πс, получим .

7) Определение . Используя свойство равенства углов подобных фигур, на плане ускорений построим фигуру аbсd подобную фигуре АВСD механизма. Соединив точку d с центром плана ускорений π, получим ускорение. Модуль ускорения точки D определим по формуле

.