3.4.6. План скоростей и его свойства

Скорости точек тела можно определить графически, построением плана скоростей. Планом скоростей называется диаграмма, на которой от некоторого центра О отложены векторы скоростей всех точек тела.

Пусть известны , , - скорости точек А, В, С тела (рис. 3.21, а). Тогда соответствующий план скоростей получим, отложив от некоторого центра О (рис. 3.21, б) в выбранном масштабе отрезки , , .

Точка О, из которой исходит пучок абсолютных скоростей, называется полюсом плана скоростей.

Установим свойства и правила построения плана скоростей. По теореме о сложении скоростей (3.30) и (3.31) имеем:

, (а)

г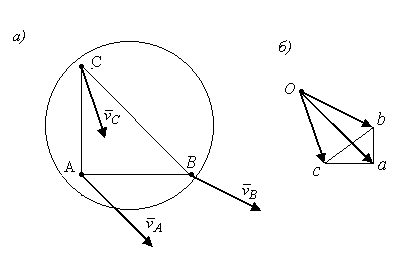 де , .

Рис. 3.21

Но из треугольника аОb имеем,

или

. (б)

Сравнивая равенства (а) и (б) устанавливаем, что ; аналогично найдем ; и т.д.

Тогда по формулам (3.31) имеем:

и ,

и ,

и .

Откуда

(3.32)

Таким образом:

• Каждый из отрезков, соединяющих вершины плана скоростей, геометрически равен вращательной скорости соответствующей точки фигуры вокруг другой точки как вокруг полюса и по модулю пропорциональны этим отрезкам .

• Отрезки, соединяющие концы векторов на плане скоростей, перпендикулярны отрезкам, соединяющим соответствующие точки тела, и по модулю пропорциональны этим отрезкам , .

• Фигуры, обозначенные на плане скоростей и в сечении (S) тела одинаковыми буквами будут при этом подобны и повернуты относительно другой на 90˚.

План скоростей плоского механизма строится как совокупность планов скоростей отдельных его звеньев, причем все векторы скоростей откладываются от общего полюса О в одном масштабе.

Планом скоростей механизма называют графичес-кое построение, представляющее собой плоский пучок, лучи которого изображают абсолютные скорости то-чек звена, а отрезки, соединяющие концы лучей, изобра-жают относительные скорости соответствующих точек в данном положении звена.

Отметим основные свойства плана скоростей меха-низма:

1. векторы абсолютных скоростей точек выходят из полюса плана скоростей;

2. векторы относительных скоростей точек одного и того же звена изображаются отрезками, соединяющими концы векторов абсолютных скоростей;

3. отрезки прямых линий (треугольники или много-угольники), соединяющие точки одного звена на плане механизма, и отрезки прямых линий, соединяющих кон-цы векторов скоростей этих точек на плане скоростей, образуют подобные и сходственно расположенные фигуры;

4. фигура на плане скоростей повернута относитель-но подобной фигуры механизма на 90° по направлению его угловой скорости;

5. порядок букв при обходе в одном направлении контуров неизменяемой фигуры и ее плана скоростей одинаков. При этом обход надо начинать с одной и той же буквы.

Эти свойства дают возможность определить ско-рость любой точки звена, если известны скорости двух точек этого звена. Рассмотрим пример построения плана скоростей.

Пример: Построить план скоростей механизма (рис. 3.22, а) для положения, изображенного на чертеже, если скорость конца кривошипа ОА известна. Кривошип О₁В соединен шарниром с серединой шатуна АС.

Решение:

1) Выбрав масштаб длин (например: в 1 см на рисунке изображено 0,1 м размера звена), изображаем механизм в дан-ном положении (рис. 3.22, а).

2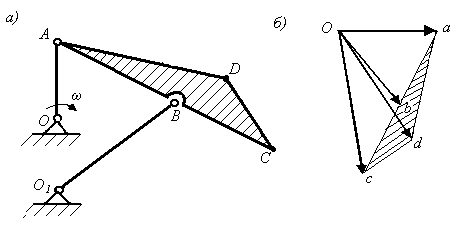 ) Определение скорости . Выбираем масштаб скорос-тей (например, 1 см на плане изображает скорость 0,5 м/с) и откладываем в этом масштабе от некоторого центра О вектор , направленный перпендикулярно к ОА (рис. 3.22, б). Из того же центра проводим прямую (скорость точки ), а из точки а прямую до пересечения с линией Оb. Тогда согласно (б) точка b и даст конец вектора .

Рис. 3.22

3) Определение скорости . Точка С механизма лежит на прямой АВС. Следовательно, по свойству подобия точка с на плане скоростей должна лежать на прямой аbс. При этом согласно (3.32)

.

Так как АВ = ВС, то откладывая на продолжении аb отре-зок bс = аb, находим точку с. Соединив точки О и с, получим вектор .

4) Определение скорости . Из точки а проводим пря-мую перпендикулярную АD, а из точки с – прямую перпенди-кулярную СD. Пересечение этих перпендикуляров дает, согла-сно (б) точку d. Соединяя точки О и d, находим вектор .