
- •3.4. Плоское движение твердого тела.
- •3.4.1. Уравнения плоскопараллельного движения
- •3.4.2. Разложение ппд на поступательное и вращательное движения
- •3.4.3. Независимость угловой скорости фигуры от выбора полюса
- •3.4.4. Определение траектории точек тела
- •3.4.5. Определение скоростей точек тела
- •3.4.6. План скоростей и его свойства
- •3.4.7. Мгновенный центр скоростей
- •Вопросы для повторения
- •3.4.8. Теорема об ускорениях точек плоской фигуры и ее следствия
- •3.4.9. Мгновенный центр ускорений
- •3.4.10. План ускорений и его свойства
- •Вопросы для повторения
- •3.5.* Сферическое движение твердого тела
- •3.6.* Общий случай движения свободного твердого тела
- •3.7. Сложное движение точки
- •3.7.1. Относительное, переносное и абсолютное движения точки
- •3.7.2. Теорема о сложении скоростей
- •3.7.3. Теорема о сложении ускорений (теорема Кориолиса)
- •3.7.4. Ускорение Кориолиса
- •Вопросы для повторения
3.7.4. Ускорение Кориолиса
Ускорением Кориолиса называется составляющая абсолютного ускорения точки в ее сложном движении, равная удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки:
. (3.63)
Появление поворотного ускорения обусловлено двумя причинами:
вследствие относительного движения точки, перемещающейся по отношению к подвижной системе отсчета, изменяется переносная скорость точки;
2) вследствие вращательного переносного движения дополнительно изменяется направление относительной скорости по отношению к неподвижной системе отсчета.
Например, если человек движется равномерно вдоль радиуса платформы вращающейся с постоянной угловой скоростью, то его относительной скоростью является скорость его движения вдоль радиуса, а переносной – скорость той точки платформы, где человек находится в данный момент (рис. 3.41).
Пусть в момент t человек занимает положение М, а в момент t + Δt – положение М1.
Так
как относительное движение равномерное
и пря-молинейное, то относительное
ускорение человека равно нулю. Однако,
благодаря вращению платформы, за время
Δt относительная скорость изменяется
по направлению от
![]() до
до
![]() .
.
З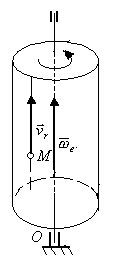 а
это же время Δt происходит изменение
модуля переносной скорости от
а
это же время Δt происходит изменение
модуля переносной скорости от
![]() до
до![]() ,
благодаря относительному перемещению
человека из точки М в точку М1.
Указанные изменения
и
,
благодаря относительному перемещению
человека из точки М в точку М1.
Указанные изменения
и![]() вызы-вают появление ускорения Кориолиса.
вызы-вают появление ускорения Кориолиса.

Рис. 3.41 Рис. 3.42
Модуль ускорения Кориолиса (3.63) определяется как модуль векторного произведения
![]()
![]() .
(3.64)
.
(3.64)
Ускорение Кориолиса равно нулю в трех случаях:
если
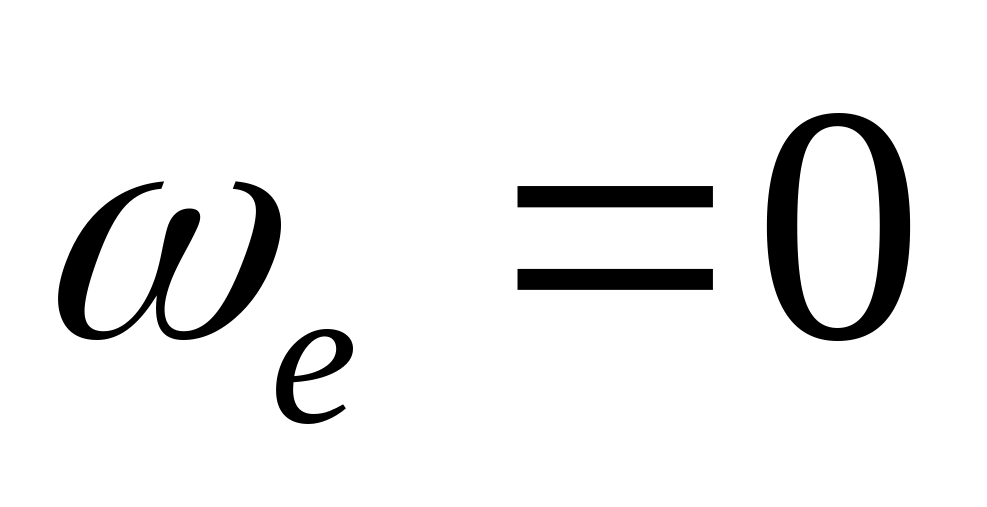 ,
то есть в случае поступательного
пере-носного движения или в моменты
времени, когда угловая скорость
непоступательного переносного движения
обращается в нуль;
,
то есть в случае поступательного
пере-носного движения или в моменты
времени, когда угловая скорость
непоступательного переносного движения
обращается в нуль;
если
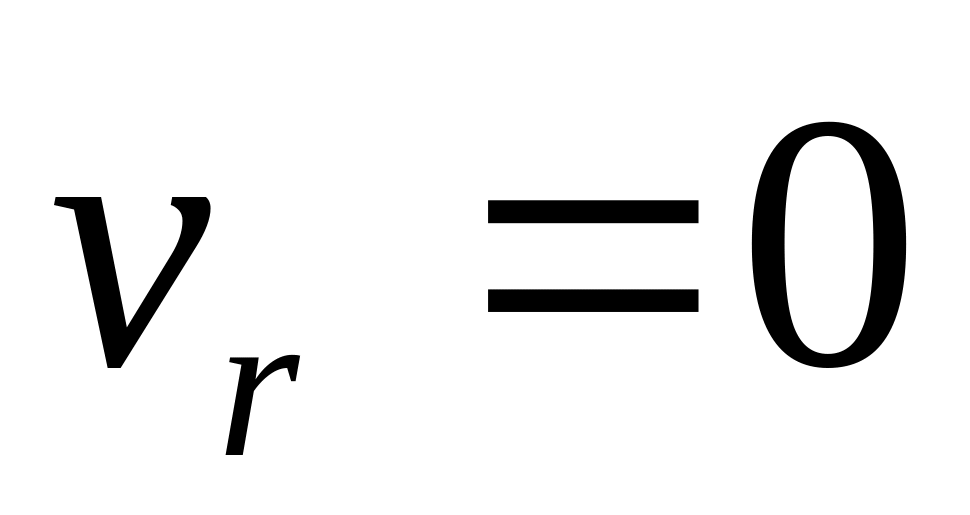 ,
то есть в случае относительного покоя
точки или в моменты времени, когда
относительная скорость обращается в
нуль;
,
то есть в случае относительного покоя
точки или в моменты времени, когда
относительная скорость обращается в
нуль;если
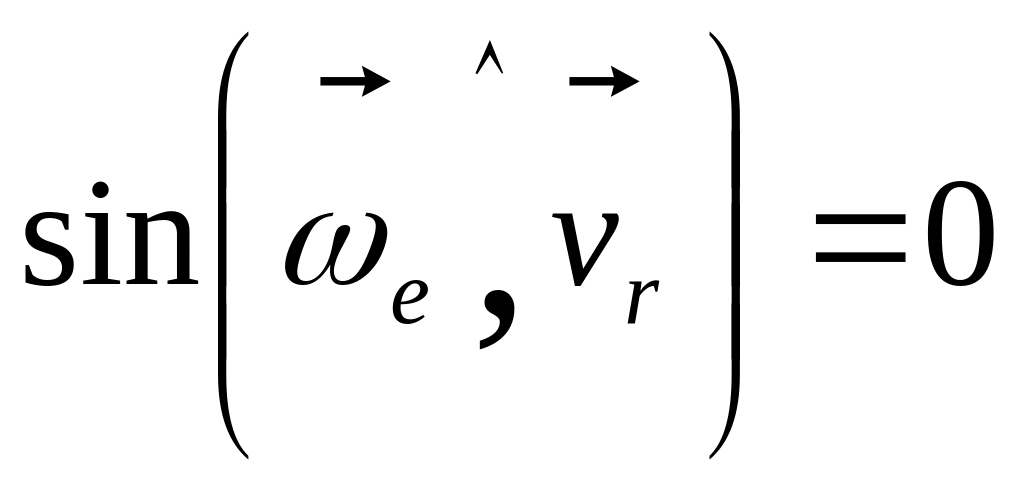 ,
то есть когда векторы
,
то есть когда векторы
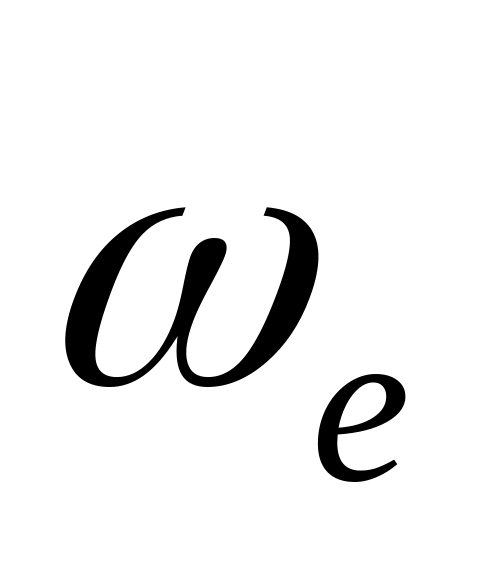 и
и
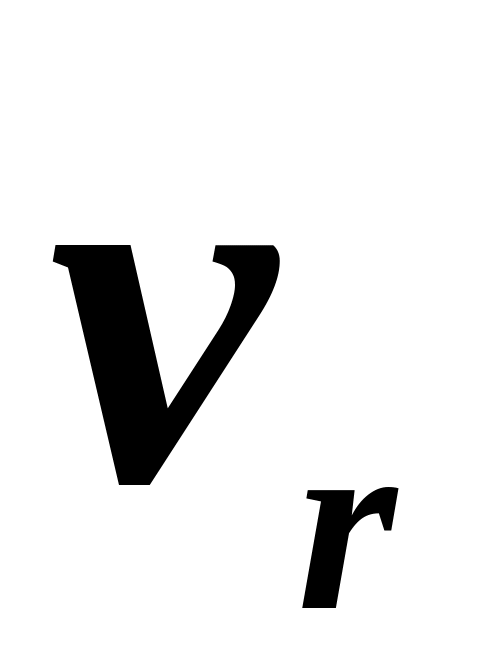 параллельны, то есть относительная
скорость точки параллельна оси
переносного вращения, как например,
при движении точки М вдоль образующей
вращающегося цилиндра (рис. 3.42).
параллельны, то есть относительная
скорость точки параллельна оси
переносного вращения, как например,
при движении точки М вдоль образующей
вращающегося цилиндра (рис. 3.42).
Н аправление
ускорения Кориолиса определяется по
правилу векторного произведения. По
этому правилу (рис. 3.43) вектор
аправление
ускорения Кориолиса определяется по
правилу векторного произведения. По
этому правилу (рис. 3.43) вектор
![]() направлен перпендикулярно плоскости,
проходящей через векторы
направлен перпендикулярно плоскости,
проходящей через векторы![]() и
и
![]() так, чтобы видеть поворот вектора
так, чтобы видеть поворот вектора
![]() к
проис-ходящим против хода часовой
стрелки.
к
проис-ходящим против хода часовой
стрелки.
Направление вектора ускорения Кориолиса можно определить по
Рис. 3.43 правилу
Жуковского (рис. 3.43): для
определения направления вектора
ускорения Кориолиса необходимо вектор
спроектировать на плоскость,
перпендикулярную вектору
![]() и повернуть проекцию в сторону вращения
на 90.
и повернуть проекцию в сторону вращения
на 90.![]()
Для иллюстрации правила Жуковского
рассмотрим пример. Предположим, что
диск вращается вокруг оси, перпендикулярной
его плоскости, по часовой стрелке с
угловой скоростью
,
а по хорде диска KL
движется точка М (рис. 3.44). Определим
модуль и направление поворотного
ускорения точки М в положении,
указанном на рисунке, если относительная
скорость точки в этот момент равна
![]() .
.
Т ак
как точка движется в плоскости диска,
перпенди-кулярной его оси вращения, то
ак
как точка движется в плоскости диска,
перпенди-кулярной его оси вращения, то
![]() и модуль пово-ротного ускорения равен
ак=2ωеvr.
Направление поворо-тного ускорения
и модуль пово-ротного ускорения равен
ак=2ωеvr.
Направление поворо-тного ускорения
![]() получаем, повернув в плоскости диска
вектор
по часовой стрелке на 90○.
получаем, повернув в плоскости диска
вектор
по часовой стрелке на 90○.
Рис. 3.44 Таким образом, при плоском
относительном движении, когда траектория
точки плоская кривая, вектор относительной
скорости
![]() перпендикулярен вектору угловой
переносной скорости
перпендикулярен вектору угловой
переносной скорости
![]() .
Тогда направление ускорения Кориолиса
можно определить, повернув вектор
относительной скорости
на 900 в сторону переносного
вращения.
.
Тогда направление ускорения Кориолиса
можно определить, повернув вектор
относительной скорости
на 900 в сторону переносного
вращения.
