2.1.3. Годограф векторної функції

Введемо поняття годографа функції . Це поняття для векторної функції аналогічне поняттю графіка скалярної функції . Якщо – неперервна функція, то неперервній зміні аргумента відповідає неперервна зміна функції . Ця зміна визначається графіком.

Р

Рисунок 2.4

озглянемо векторну функцію . Надаючи аргументу значення , дістанемо відповідні значення функції . Проведемо з фіксованої точки О вектори . Якщо аргумент змінюється неперервно від до , то кінець вектора опише відрізок кривої, що називається годографом векторної функції. Отже,

годографом векторної функції скалярного аргумента називають криву, що її викреслює кінець радіуса-вектора, який приймає значення вектора при неперервній зміні аргумента .

Щоб знайти рівняння годографа в параметричному вигляді, досить вибрати довільну ортогональну систему координат з початком у точці О і знайти проекції вектора на ці координатні осі.

Рівняння

. (2.13)

є скалярними рівняннями годографа векторної функції .

Розглянемо похідну від функції . Похідною векторної функції за часом називають змінний вектор, що визначається рівністю

, (2.14)

якщо границя в правій частині (2.14) існує.

Доведемо, що похідна є вектором, напрямленим по дотичній до годографа функції .

Розглянемо приріст аргумента і відповідний йому приріст функції . Певному значенню функції відповідає точка М її годографа (рис. 2.5). Векторові відповідає точка годографа. Відношення є вектором, нап-рямленим по січній годографа функції . Якщо , а точка , то січна наближається до дотичної в точці М. Отже, вектор напрямлений по дотичній до годографа функції .

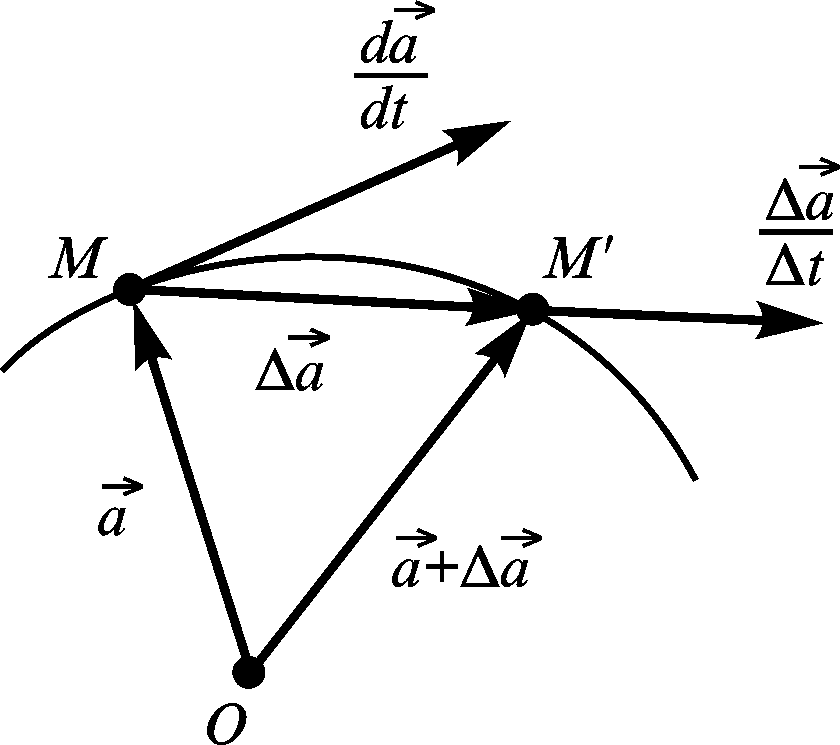
Рисунок 2.5

Як відомо, похідна від скалярної функції визначає напрям дотичної до графіка функції, а її фізичний зміст полягає у визначенні зміни функції залежно від зміни аргумента. Отже, фізичний зміст похідної векторної функції можна вважати аналогічним – похідна векторної функції визначає зміну вектора за часом t і напрямлена по дотичній до годографа функції .

2.1.4. Швидкість руху точки

Перейдемо до вивчення основних кінематичних величин, що характеризують рух точки в просторі. Такими величинами є швидкість точки та її прискорення.

Як і в підрозділі 2.1.2, скористаємось трьома способами визначення руху точки.

Швидкістю точки називають фізичну величину, що характеризує зміну положення точки в просторі, що визначається радіусом-вектором, зі зміною часу.

При векторному способі визначення руху точки закон її руху має вигляд

.

Траєкторія точки – годограф функції .

На основі визначення поняття швидкості і фізичного змісту похідної векторної функції скалярного аргумента робимо висновок, що

швидкість точки є вектор, який дорівнює похідній за часом від радіуса-вектора:

. (2.15)

Т

Рисунок 2.6

ут і далі диференціювання за часом позначено крапкою.

Вектор швидкості напрямлений по дотичній до годографа вектора , тобто по дотичній до траєкторії точки в той бік, що відповідає зростанню часу (рис. 2.6).

Рівність (2.15) визначає вектор швидкості точки векторним способом математичного опису її руху.

Розглянемо визначення швидкості координатним способом. З рівностей (2.7) і (2.15) маємо

.

Розкладаючи вектор по ортах ортогональної системи декартових координат

і порівнюючи вирази, маємо

. (2.16)

За відомими проекціями вектора швидкості на координатні осі, легко знайти модуль вектора швидкості і його напрямні косинуси:

; (2.17)

. (2.18)

Рівності (2.16)-(2.18) визначають вектор швидкості точки координатним способом математичного опису її руху.

Знайдемо швидкість, припускаючи, що рух точки задано натуральним способом. Розглядаючи радіус-вектор точки як складну функцію часу, згідно рівностей (2.8), (2.10) і (2.15) дістанемо

.

З’ясуємо зміст кожного співмножника останньої рівності.

Розглянемо вектор

. (2.19)

На підставі змісту підрозділу 2.1.3 твердимо, що цей вектор напрямлений по дотичній до траєкторії у бік додатних дугових координат. Справді, якщо , то вектор напрямлений у бік додатних дугових координат (рис. 2.7). У цей самий бік напрямлений і вектор . Зі зміною знака змінюється і знак . Отже, напрям залишається попереднім. Модуль вектора дорівнює одиниці:

,

оскільки є довжиною хорди (рис. 2.7).

Рисунок 2.7

Отже, — орт дотичної до траєкторії.

На підставі викладеного дістанемо

. (2.20)

Щоб визначити , домножимо рівність (2.20) скалярно на вектор :

. (2.21)

Отже, є проекцією швидкості на дотичну до траєкторії. Таким чином,

. (2.22)

Рівності (2.20)-(2.22) визначають вектор швидкості точки натуральним способом математичного опису її руху.