2.2.14. Розподіл швидкостей і прискорень точок тіла з нерухомою точкою

За формулою (2.83) визначають швидкість довільної точки тіла:

. (2.90)

Початок нерухомої системи координат збігається з нерухомою точкою. Проектуючи ліву і праву частини рівності (2.90) на осі , визначимо проекції швидкості точки М на ці осі:

;

(2.91)

.

Прискорення довільної точки М визначається за (2.84)

.

Цей вираз можна переписати інакше:

. (2.92)

Перший доданок у (2.92) називають обертальним прискоренням, другий — доосьовим

. (2.93)

Напрями прискорень і повністю визначаються за (2.93). З виразу доосьового прискорення видно, що

вектор лежить у тій площині, в якій лежать вектори і , і напрямлений по перпендикуляру до вектора (рис. 2.44), тобто по перпендикуляру до миттєвої осі обертання.

Модулі складових обертального і доосьового прискорень точки можна визначити за формулами:

; (2.94)

. (2.95)

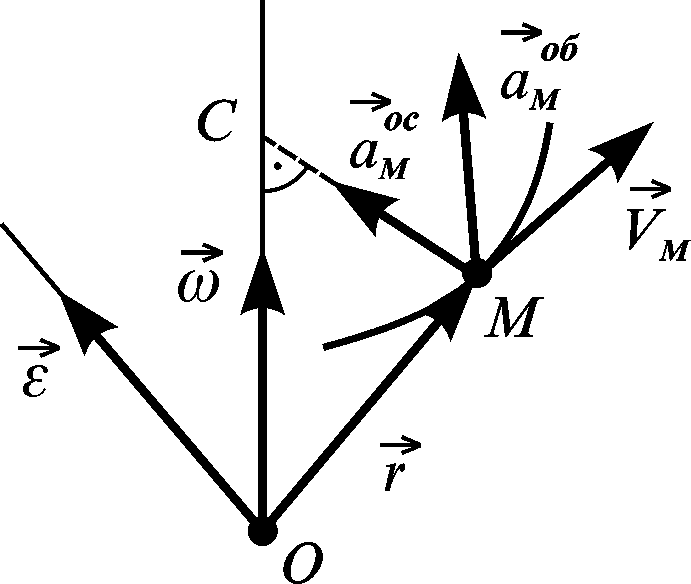
Рисунок 2.44

Приклад 2.7. Конус з висотою 4 м і радіусом основи 3 см котиться по площині без ковзання, маючи нерухому вершину в точці О (рис. 2.45).

Визначити кутову швидкість , кутове прискорення конуса, а також швидкість і прискорення його точок і , якщо швидкість центра основи конуса см/с = const.

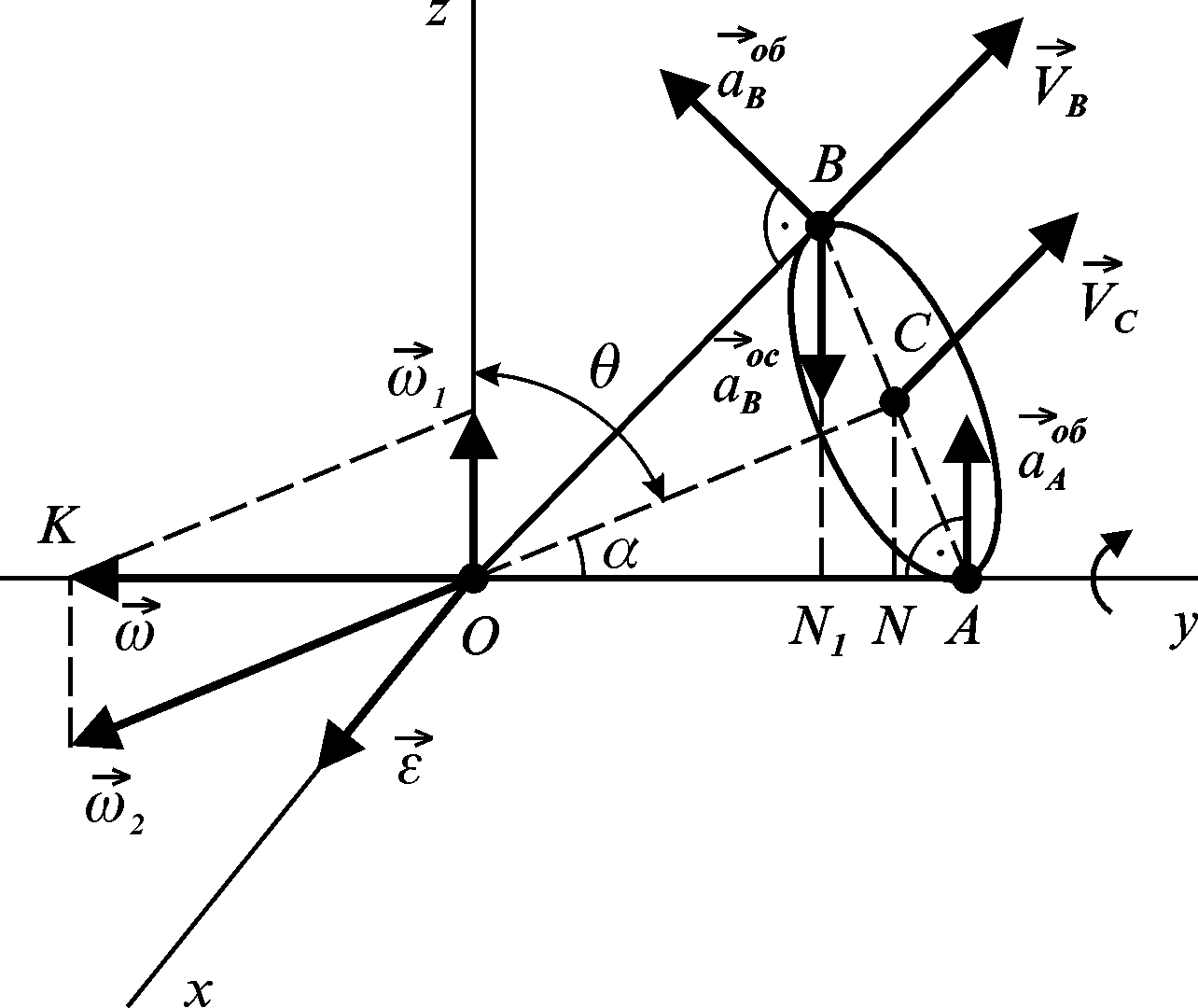
Рисунок 2.45

Розв’язання. На підставі теореми Пуансо твердимо, що бічна поверхня конуса є рухомим аксоїдом, а площина – нерухомим аксоїдом. Миттєва вісь обертання – твірна конуса . Вектор спрямований вздовж миттєвої осі обертання (рис. 2.45). Згідно формули Ейлера (2.54)

, .

Швидкість точки С спрямована протилежно осі .

Величину знаходимо з прямокутного трикутника :

см.

Отже,

рад/с.

Кут утворений осями: прецесії і власного обертання , є кутом нутації . Оскільки він залишається незмінним, має місце регулярна прецесія. Отже, кутова швидкість є сумою двох складових: кутової швидкості прецесії і кутової швидкості власного обертання :

.

Як видно з рис. 2.45, трикутник, утворений векторами , і , подібний до , сторони якого відомі: = 4 см, см, см. Елементарні геометричні міркування дають змогу знайти

рад/с; рад/с.

Кутове прискорення можна розглядати як швидкість точки , що викреслює годограф вектора кутової швидкості . Тому за формулою Ейлера

.

Вектор напрямлений по дотичній до годографа , тобто перпендикулярно до вектора . Модуль

рад/с².

Швидкість точки дорівнює нулеві. Ця точка належить миттєвій осі обертання.

Швидкість точки конуса знаходимо як швидкість миттєвого обертання точки навколо миттєвої осі . За формулою Ейлера запишемо пропорцію

.

Оскільки , то см/с. Швидкість точки паралельна швидкості точки .

Прискорення точок А і В знайдемо за формулами:

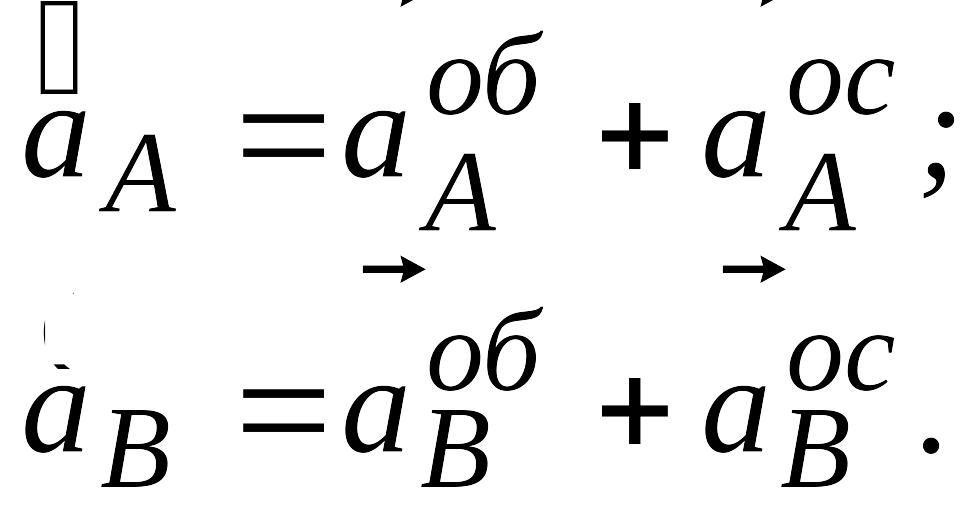
Обчислимо кожний доданок і визначимо напрям.

Напрями доосьових прискорень знаходимо за правилом векторного добутку:

;

.

Як було зазначено, , тому .

Доосьове прискорення точки напрямлене вздовж миттєвого радіуса обертання точки до миттєвої осі .

Величина см/с².

Обертальне прискорення ; .

Величина см/с².

Оскільки , то см/с².

Напрями і знаходимо за правилом векторного добутку. Ці прискорення знаходяться в площині трикутника і перпендикулярні і відповідно.

Отже, , см/с².

Величину прискорення точки знаходимо за теоремою косинусів:

см/с².