Свойства преобразования Лапласа

При осуществлении преобразования Лапласа и выполнении математических операций с оригиналами и изображениями используются следующие свойства преобразования Лапласа.

1. Линейность преобразования Лапласа.

,

где  произвольные комплексные числа, F(p); (p) – изображения оригиналов f(p) и (t) соответственно.

Изображение линейной комбинации оригиналов равно такой же линейной комбинации их изображений.

2. Дифференцирование оригинала

n – кратному дифференцированию оригинала соответствует умножение изображения на pⁿ.

3. Интегрирование оригинала

Интегрированию интеграла в пределах от 0 до t соответствует деление изображения на р.

4. Смещение аргумента оригинала

, при этом , если .

Смещению аргумента оригинала на соответствует умножение изображения на .

5. Смещение аргумента изображения

Смещению аргумента изображения на соответствует умножение оригинала .

6. Умножение изображений (теория свертывания)

Операция называется сверткой.

Изображение свертки двух оригиналов равно произведению их изображений.

Переход от изображения к оригиналу осуществляется с помощью обратного преобразования Лапласа, выполняемого с использованием формулы обращения:

где С – абсцисса абсолютной сходимости, выбирается так, чтобы все полюсы подынтегральной функции находились слева от нее (рис. 28). Всегда должно быть С > s₀. На рис. 28  – полюсы функции-изображения.

О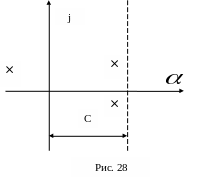 бозначение обратного преобразования Лапласа осуществляется символом L^-1 или 1/L.

.

Непосредственное использование формулы обращения вызывает значительные сложности. Для упрощения обратного перехода используются таблицы, приводимые в справочниках, и специальные приемы.

Так, если функция-изображение является дробной функцией: , то при выполнении обратного преобразования Лапласа применимо разложение Хевисайда. Пусть функция имеет m полюсов (корней уравнения B(p)=0), тогда

Пример. Выше мы получили для постоянной величины

Осуществим обратное преобразование Лапласа, используя разложение Хевисайда. В этом случае A(p)=A, B(p)=p, p_k=0, m=1,

, следовательно,

В результате обратного преобразования с использованием разложения Хевисайда получена постоянная величина А, что и следовало ожидать.

Пример исследования функционального элемента

Рассмотрим электрический функциональный элемент, принципиальная и структурная схемы которого изображены на рис. 29.

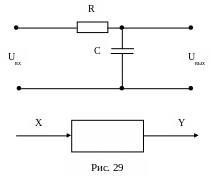
Для этого элемента

; ^U_вх^=iR+U_вых^.

Представим

отсюда

В результате получаем следующее дифференциальное уравнение, описывающее элемент:

.

Представим уравнение в операторном виде:

,

где  постоянная времени, , .

Решим полученное дифференцированное уравнение обычными методами. Приняв , запишем уравнение в виде

Для решения уравнения введём новую переменную , поскольку , то

.

Решение полученного однородного уравнения

Для нахождения постоянной интегрирования D учтем начальные условия: при , , следовательно, и , .

Итак, , откуда окончательно получаем

.

Найдём решение, используя преобразование Лапласа. Для области изображений Лапласа

Подвергнем исходное уравнение преобразованию Лапласа

.

Получено алгебраическое уравнение, которое легко решается относительно изображения выходной величины:

Мы получим решение дифференциального уравнения в изображениях. Обратный переход к оригиналу может быть осуществлен с использованием разложения Хевисайда

A(p)=A, B(p)=p(T_p+1).

Функция-изображение имеет два полюса, получаемые из решения уравнения

B(p)=p(T_p+1)=0: p₁ =0, p₂= - 1/T.

Тогда

Используем общую формулу и получим

Итак, в обоих случаях мы получим одно и то же решение:

или .

Используя полученное решение, ответим на следующие вопросы.

1. Как будет изменяться во времени выходное напряжение элемента, если в момент t=0 на вход подать напряжение U_вх=100 B? При этом R=1 МОм, С=1 мкФ. Для данных значений T =RC =10⁶ 10^-6 =1c; 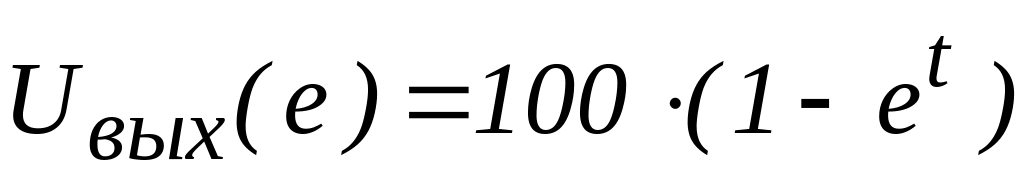B.

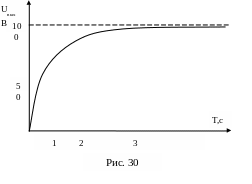
График переходного процесса показан на рис. 30. Процесс имеет плавный апериодический характер. Постоянное напряжение на выходе исследуемой цепи устанавливается через 3,5 с (примерно).

2. Через какое время напряжение на выходе будет отличаться от входного не более чем на 0,1 В?

3. Какова будет наибольшая относительная погрешность выходного напряжения, при подаче на вход элемента импульса 100 В длительностью 3 с?

U_вых= 100(1-е^-3) = 95,0 ,

.

В рассматриваемом примере исследован простейший элемент. Однако порядок исследования и используемые методы являются общими как для более сложных элементов, так и для систем САУ.