Імпульс.

Векторна величина , що дорівнює добутку маси m матеріальної точки на її швидкість , і що має напрям швидкості, називається імпульсом, або кількістю руху, цієї матеріальної точки.

.

Другий закон Ньютона.

Другий закон Ньютона — основний закон динаміки поступального руху — відповідає на питання, як змінюється механічний рух матеріальної точки (тіла) під дією прикладених до неї сил.

Прискорення, що набуває матеріальна точка (тіло), пропорційне діючий на неї силі, співпадає з нею по напрямку і обернено пропорційне до маси матеріальної точки (тіла)

,

або

.

Більш загальне формулювання другого закону Ньютона: швидкість зміни з часом імпульсу матеріальної точки дорівнює діючій на неї силі.

Векторна величина називається елементарним імпульсом сили за малий час dt її дії. Імпульс сили за проміжок часу t = t₂ – t₁ визначається інтегралом 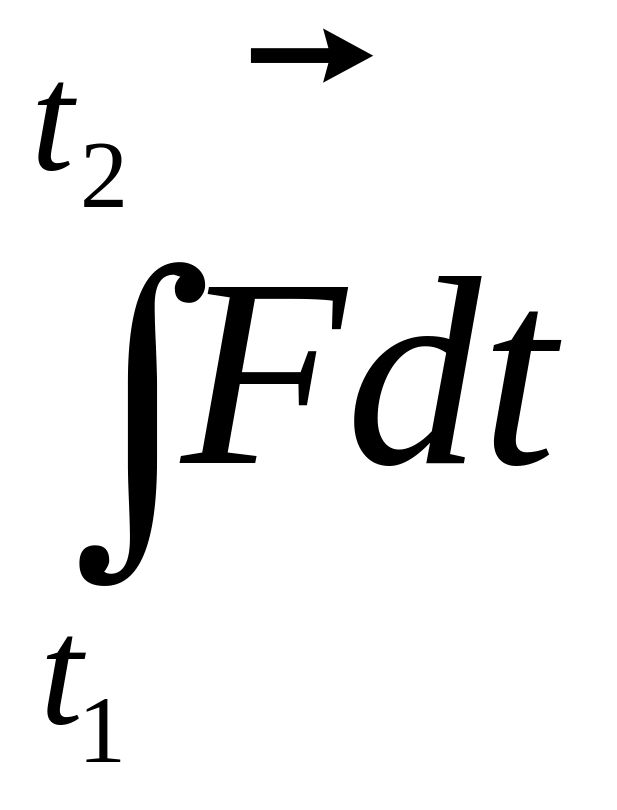. Згідно другому закону Ньютона зміна імпульсу матеріальної точки дорівнює імпульсу діючої на неї сили:

;

Основний закон динаміки матеріальної точки виражає принцип причинності в класичній механіці — однозначний зв'язок між зміною з часом стану руху і положення в просторі матеріальної точки і діючою на неї силою, що дозволяє, знаючи початковий стан матеріальної точки, описати її стан в будь-якій подальший момент часу.

Принцип незалежності дії сил.

У механіці велике значення має принцип незалежності дії сил: якщо на матеріальну точку діє одночасно декілька сил, то кожна з цих сил завдає їй прискорення згідно другому закону Ньютона, неначе інших сил не було. Згідно цьому принципу сили і прискорення можна розкладати на складові, використання яких приводить до істотного спрощення розв'язків задач.

Наприклад, нормальне і тангенціальне прискорення матеріальної точки визначаються відповідними складовими сили:

; ; .

; ; .

Сила , що надає матеріальній точці нормальне прискорення, спрямована до центру кривизни траєкторії і тому називається доцентровою силою.

Третій закон Ньютона.

Всяка дія матеріальних точок (тіл) одна на одну має характер взаємодії – сили з якими діють одна на одну матеріальні точки, завжди рівні по модулю, протилежно направлені і діють вздовж прямій, що сполучає ці точки.

Ці сили прикладені до різних матеріальних точок (тіл), завжди діють парами і є силами однієї природи.

Третій закон Ньютона дозволяє перейти від динаміки окремої матеріальної точки до динаміки довільної системи матеріальних точок, оскільки дозволяє звести будь-яку взаємодію до сил парної взаємодії між матеріальними точками.

Закон збереження імпульсу.

Імпульс замкнутої системи не змінюється з часом (зберігається)

.

Закон збереження імпульсу є наслідком однорідності простору: при паралельному перенесенні в просторі замкнутої системи тіл як цілого її фізичні властивості не змінюються (не залежать від вибору положення початку координат інерціальної системи відліку).

Закон руху центру мас.

У механіці Ньютона, завдяки незалежності маси від швидкості, імпульс системи може бути виражений через швидкість її певної точки – центру мас. Центр мас (або центр інерції) системи матеріальних точок є деяка уявна точка С, координати якої характеризують розподіл маси цієї системи. Положення центру мас (радіус-вектор цієї точки) визначається наступним чином

,

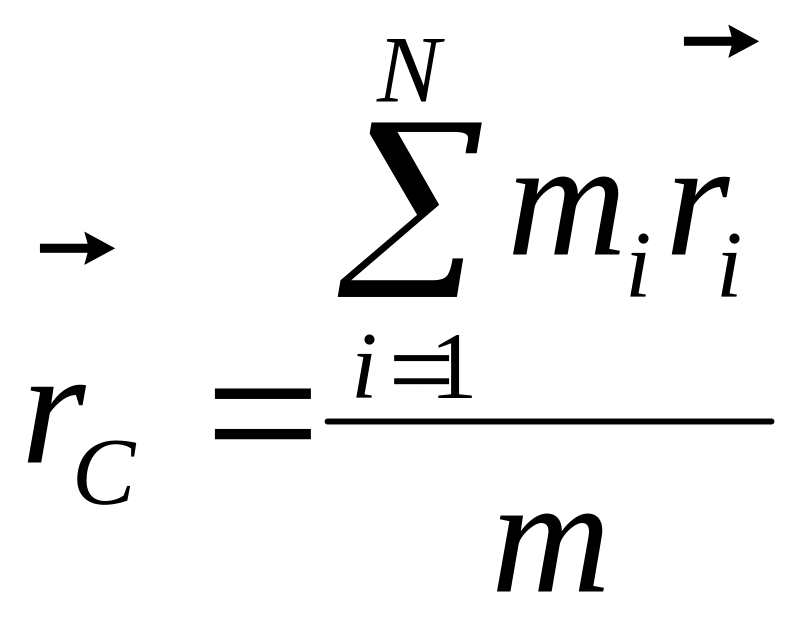де і — відповідно маса і радіус-вектор і-ої матеріальної точки; N — число матеріальних точок в системі; — маса всієї системи.

Імпульс всієї системи буде імпульсом цієї точки – центра мас – коли її маса дорівнює масі системи

.

Закон руху центру мас: центр мас системи рухається як матеріальна точка, в якій зосереджена маса всієї системи і на яку діє сила, рівна геометричній сумі всіх зовнішніх сил, що діють на систему.

.

Із закону збереження імпульсу виходить, що центр мас замкнутої системи або рухається прямолінійно і рівномірно, або залишається нерухомим.