Кінематика обертального руху.

З міну положення тіла у просторі за час t при обертанні задають вектором кутового переміщення модуль якого дорівнює куту повороту (в радіанах), а напрям співпадає з напрямом поступального руху вздовж осі обертання правого гвинта (рис. 1.4). За елементарний проміжок часу dt тіло здійснює нескінченно мале кутове переміщення .

Кутовою швидкістю називають величину, що дорівнює куту повороту тіла в одиницю часу.

Вектор миттєвої кутової швидкості є похідною від куту повороту тіла по часу

.

Вектор завжди спрямований вздовж осі обертання так само як і вектор , тобто по правилу правого гвинта, а його модуль дорівнює куту повороту тіла в одиницю часу

.

Зміну кутової швидкості з часом характеризує кутове прискорення. Вектор кутового прискорення є похідною від вектора кутової швидкості (другою похідною куту повороту) по часу

.

Якщо вісь обертання нерухома, то вектор направлений уздовж осі обертання в сторону вектора приросту кутової швидкості ( спрямований так саме як при прискореному обертанні і протилежно – при сповільненому). При цьому його модуль дорівнює похідній від модуля кутової швидкості

.

Одиниці кутової швидкості і кутового прискорення – рад/с і рад/с², відповідно.

Якщо відома залежність кутового прискорення з часом, то можна знайти приріст кутової швидкості тіла за будь-який проміжок часу t (від t₁ до t₂)

.

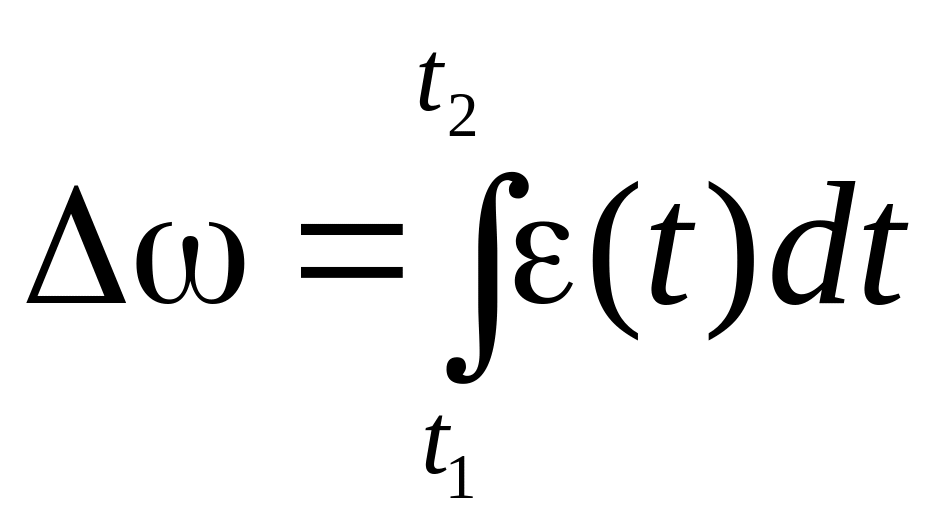Інтеграл кутової швидкості в інтервалі часу t дає кут на який повернеться тіло за цей час

.

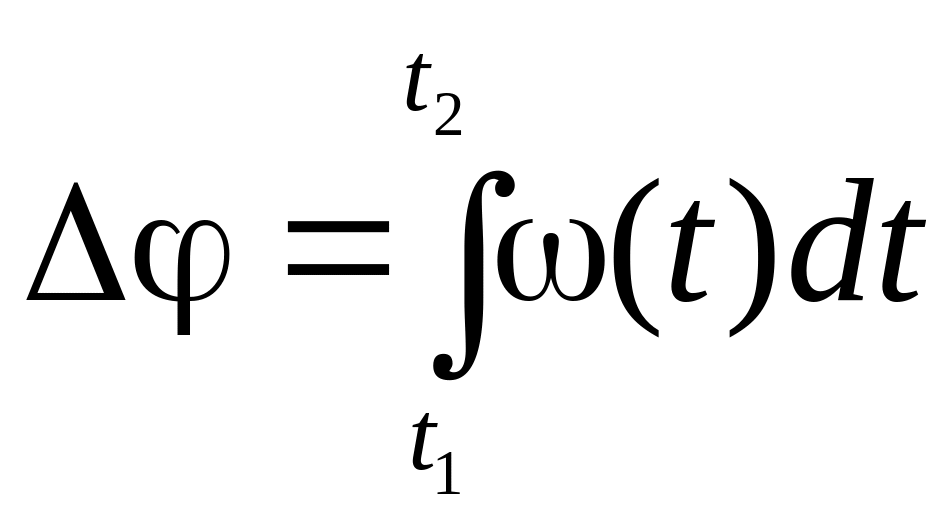При рівномірному обертанні: , тобто .

Рівномірне обертання можна характеризувати також періодом обертання Т –  часом, за який точка здійснює один повний оберт

Частота обертання - число обертів, що здійснюються тілом в одиницю часу

Одиниця частоти обертання - герц (Гц).

При рівноприскореному обертальному русі :

; .

Зв'язок лінійних і кутових характеристик руху.

Коли тіло здійснює кутове переміщення будь-яка його точка на відстані R від осі обертання пройде по своїй траєкторії – колу шлях (рис. 1.4)

.

Миттєва лінійна швидкість точки теж пов'язана з кутовою швидкістю і радіусом траєкторії співвідношенням

.

У векторному вигляді формулу для лінійної швидкості можна написати як векторний добуток:

.

За визначенням векторного добутку (див. Додаток 3) його напрям співпадає з напрямом поступального руху правого гвинта при його обертанні від до (рис. 1.5).

При обертанні кожна точка тіла рухається по колу, а тому має певне нормальне прискорення

.

Якщо тіло обертається з кутовим прискоренням , то кожна його точка на відстані R від осі обертання рухається з тангенціальним прискоренням

,

або у векторному вигляді

.

Приклади розв'язування задач.

Приклад 1. Точка рухається по прямій лінії згідно з рівнянням x = 6t – t³/8 (довжина вимірюється в метрах, час – в секундах). Визначити середній модуль швидкості руху точки в інтервалі часу від t₁ = 2 с t₂ = 6 c.

А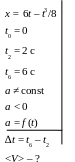 наліз і розв’язання.

Т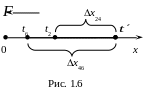 очка рухається прямолінійно вздовж горизонтальної осі Оx (рис. 1.6). З наведеного рівняння можна визначити положення точки в будь-який проміжок часу. Середня швидкість визначається за формулою Необхідно зробити аналіз форми руху точки. Спочатку визначаємо миттєву швидкість як похідну від координати x за незалежною змінною t:

Прискорення визначається як похідна від миттєвої швидкості за незалежною змінною t:

Рух точки сповільнений, модуль прискорення з часом зростає. Сила яка надає точці прискорення, направлена протилежно рухові.

Визначимо швидкість точки в кінці другої і шостої секунди:

м/с; м/с.

Треба узнати, в який момент часу миттєва швидкість змінює знак (+) на (–):

;

с.

В момент часу с сила зупинить точку, потім точка почне рухатися в протилежному напрямку. Прискорення не змінює напряму і гальмівна сила діє в тому ж напрямі.

;

м;

м;

 м/с;

 м/с.

Відповідь: модуль середньої швидкості дорівнює 3 м/с.

Приклад 2. Радіус-вектор матеріальної точки визначається за виразом м. Знайти швидкість V і прискорення a точки; модуль швидкості в момент с; шлях S, пройдений протягом перших 10 с руху; модуль переміщення за цей самий час. Проаналізувати знайдений результат.

А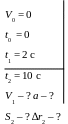 наліз і розв’язання.

Згідно з виразом в умові для радіус-вектору його проекції на вісі координат (координати матеріальної точки) знаходяться:

; ; .

Бачимо, що координата z точки залишається з часом незмінною (точка рухається в площині, перпендикулярній осі z). Крім того координати точки у початковий момент часу (t = 0):

x(0) = 0; y(0) = 0; z(0) = 7;

Визначимо миттєву швидкість як похідну від вектора за часом. Вона напрямлена у просторі по дотичній до траєкторії в бік руху:

Якщо представити вектор через його проекції на координатні вісі, то одержимо У даному випадку

; ;

В початковий момент часу точку не рухалась – .

Миттєве прискорення визначимо як першу похідну від вектора миттєвої швидкості:

Вектор миттєвого прискорення має координати

; ;

Прискорення не залежить від часу, звідси робимо висновок, що рух рівноприскорений. Так як рух відбувається із стану спокою з постійним вектором прискорення, то траєкторія повинна бути прямою. Модуль прискорення знайдемо за відомою формулою

м/с².

Значення вектора миттєвої швидкості знайдемо за формулою

;

м/с.

Рух матеріальної точки рівноприскорений без початкової швидкості. Шлях, пройдений за 10 с, визначається за формулою

м.

Модуль переміщення за перших 10 с знайдемо за формулою

м.

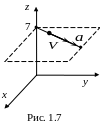
Рівність шляху S₂ і модуля радіуса-вектора переміщення підтверджує те, що розглянутий рух прямолінійний (див рис. 1.7).

Відповідь: швидкість ; прискорення м/с²; модуль швидкості через 2 с від початку руху 20 м/с; шлях, пройдений протягом перших 10 с, як і модуль переміщення, складає 500 м. Рух точки із стану спокою рівноприскорений прямолінійний в площині перпендикулярній осі z.

Приклад 3. Колесо радіусом 0,2 м обертається навколо нерухомої вісі так, що його кутова швидкість змінюється з часом за законом  с^. Знайти кутове прискорення колеса, а також лінійне прискорення точки на ободі в початковий момент часу. Скільки обертів зробить колесо до повної зупинки? Який шлях пройде точка на ободі за цей час?

Аналіз і розв’язання.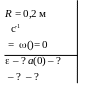

П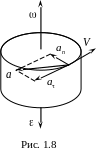 ри обертанні навколо нерухомої вісі кутове прискорення спрямоване вздовж цієї вісі, а його величина дорівнює похідній від модуля кутової швидкості

 с^.

Отже колесо обертається з постійним кутовим прискоренням. Від’ємне значення говорить про те, що обертання сповільнене, і вектор кутового прискорення направлений проти вектору кутової швидкості (рис. 1.8).

Точка на ободі при обертанні колеса рухається по колу, а її повне лінійне прискорення складається із нормального і тангенціального . Нормальне прискорення спрямоване до осі обертання і по модулю дорівнює

.

Тангенціальне прискорення точки на ободі при сповільненому обертанні спрямоване по дотичній до ободу протилежно руху і пов’язане з кутовим прискоренням

.

Модуль лінійного прискорення в початковий момент часу

3,225 м/с².

Щоб знайти кількість обертів колеса до зупинки, спочатку знайдемо момент часу , коли воно зупинилось, тобто коли кутова швидкість стала дорівнювати нулю.

,

звідки

 с.

Кут на який обернеться колесо за час від 0 до

.

Число обертів, що зробить колесо

0,64.

Шлях який пройде точка на ободі колеса теж зв’язане з кутом повороту

0,8 м.

Відповідь: Колесо обертається рівносповільнено з кутовим прискоренням 2 с^. Лінійне прискорення точки на ободі колеса в початковий момент часу складало 3,225 м/с². До повної зупинки колесо зробило 0,64 оберти, а точка на ободі пройшла шлях 0,8 м.